Câble coaxial, haut-parleur, Concours ITPE ingénieur territorial 2018. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . III. Transmission au haut-parleur. La guitare est reliée à l'amplificateur, puis au haut-parleur, par un câble coaxial. Ce câble est constitué de deux cylindres conducteurs, l'un creux ( tresse métallique) et l'autre plein ( âme), de même axe et séparés par un isolant ( diélectrique) de permitivité  er, le tout dans une gaine. Le câble est caractérisé par sa capacité linéïque g et son coefficient d'auto-inductance L. 36. Recopier et légender le schéma suivant. On donne g = 2 p e0 er / (ln(r2/r1) et L = µ0/ (2p) ln ( r2 / r1). ( capacité et inductance linéïques ) r1 rayon intérieur du diélectrique, r2 rayon extérieur du diélectrique. Le câble est considéré de longueur infinie et on néglige les effet de bords. 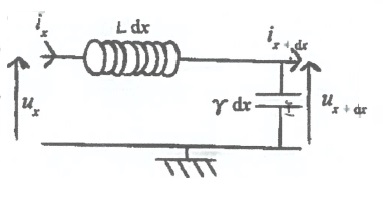Un élément de câble de longueur infinitésimale dx peut être représenté schématiquement par : r1 = 0,50 mm ; r2 =1,75 mm ; e0 = 8,85 10-12 F m-1 ; er = 2,25 ; µ0 = 4 p 10-7 H m-1. 37. Calculer g et L. g = 2 x3,14 x8,85 10-12 x2,25 / ln(1,75 / 0,50) =9,987 10-11 ~1,0 10-10 F. L = 4 x3,14 10-7 x ln(1,75 /0,5)=1,574 10-6 ~1,6 10-6 H. 38. Trouver les deux relations reliant d'une part ux+dx, ux, ix et d'autre part ix+dx, ux et ix. 39. Déterminer les équations aux dérivées partielles liant l'intensité i(x,t) et la tension u(x,t). 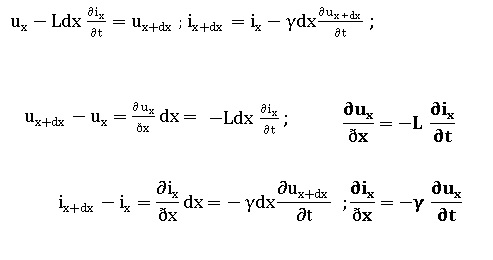40. En déduire les équations d'ondes vérifiées par i(x,t) et u(x,t). Dériver les expressions précédentes respectivement par rapport à x et à t. 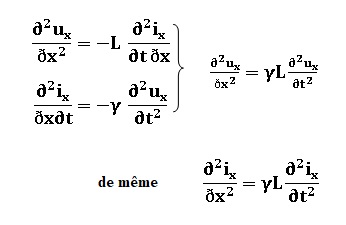41. Exprimer la vitesse de propagation v des ondes de courant et de tension en fonction de g,et L puis en fonction de er, e0 et µ0. Calculer sa valeur. v = 1 /(gL)½ = 1/ (e0 er µ0)½ = 1 / (8,85 10-12 x2,25 x4 x3,14 10-7)½ ~2,0 108 m /s.. 42. Calculer le temps de retard pour un câble de 10 m. 10 /( 2 108) = 5 10-8 s.. On considère u(x,t) une onde de tension sinusoïdale, progressive de pulsation w2, se propageant le long du câble dans le sens des x croissants. On définit en notation complexe :  u(t) = u0 exp j(w2t-k2x) et i(x,t) = i0 exp j(w2t-k2x) 43. Déterminer la relation entre w2 et k2 pour que u(x,t) et i(x,t) vérifient le système d'équations de la question 39. du / dx =-k2 u0 j  exp j(w2t-k2x) ; di /dt= w2 i0 j exp j(w2t-k2x). -k2 u0 j  exp j(w2t-k2x) = - Lw2 i0 j exp j(w2t-k2x). k2 u0 = Lw2 i0 ; k2  = Lw2 i0 / u0. di / dx =-k2 i0 j  exp j(w2t-k2x) ; du/dt= w2u0 j exp j(w2t-k2x). -k2 i0 j  exp j(w2t-k2x) = - gw2 u0 j exp j(w2t-k2x). k2 i0 = gw2 u0 ; i0 / u0 = gw2 / k2. Par suite : k2 =( Lg)½w2. 44. Montrer qu'en tout point du câble le rapport u(x,t) / i (x,t) est égal à une constante que l'on notera Rc. u(x,t) / i (x,t) =u0 / i0 =  k2 / (gw2 )= (L / g)½. 45. Calculer Rc. Rc = (1,574 10-6 / (9,987 10-11)½ = 1,26 102. On s'intéresse maintenant à l'effet de câble sur les signaux transmis selon leurs fréquences. 46. Rappeler à quoi est équivalent un condensateur en basse fréquence, puis en haute fréquence. Même question pour la bobine. Un condensateur se comporte comme un interrupteur ouvert en basse fréquence et comme un interrupteur fermé en haute fréquence. Une bobine se comporte comme un interrupteur ouvert en haute fréquence et comme un interrupteur fermé en basse fréquence. 47. Avec des schémas équivalents et sans calculs, déterminer la nature du filtre équivalent au câble coaxial. 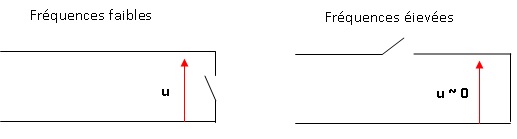Le câble coaxial se comporte comme un filtre passe bas d'ordre 2. 48. Donner sans démonstration la fréquence propre de  ce filtre w0 pour un câble de 10 m. w0 = 1 /(10( Lg)½ =1 /(10 (1,574 10-6 x 9,987 10-11)½ ~8,0 106 rad / s. f0 = w0 / (2p) =1,3 106 Hz. . 49. Ce comportement fréquentiel est-il génant pour l'utilisation qui en est faite ? Non, le câble transmet des sons audibles de fréquence inférieure à 20 kHz. Une modèlisation plus précise de l'élément de câble coaxial, prenant en compte les pertes, est faite en ajoutant une résistance rl en série avec l'inductance et une résistance rc en parallèle avec le condensateur. 50. Quelle résistance rl ou rc est la plus grande ? Justifier. Pour un câble de 10 m et une fréquence f = 104 Hz : w = 2 p f ~6 104 rad/s. Lw ~1,6 10-5 x 6 104 ~ 1 ohm ; rl doit être très inférieure à 1 ohm, de l'ordre du centième d'ohm.. 1 / (gw) = 1 / (10-9 x6 104) ~1,7 104 ohms ; rc doit être très inférieure à 1,7 104 ohms, de l'ordre de la centaine d'ohm. IV. Restitution du son par un haut-parleur. 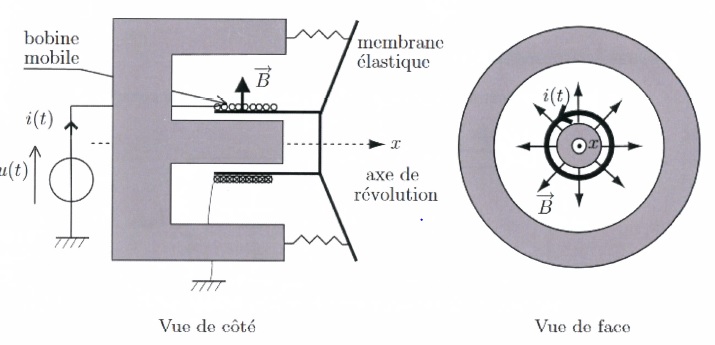Un haut-parleur électrodynamique est constitué : - d'un aimant annulaire d'axe Ox, dréant un champ magnétique radial permanent, de norme B dans l'entrefer ; - d'une bobine indéformable de même axe Ox comportant N spires de rayon a, placée  dans l'entrefer  de l'aimant ; - d'une membrane M perpendiculaire à l'axe et pouvant effectuer de faibles déplacements axiaux autour de sa position d'équilibre grâce à un assemblage se comportant comme un ressort unique de raideur k. L'ensemble mobile {bobine + membrane }, de masse m, repéré par l'abscisse x(t) est de plus soumis à une force de frottement visqueux de la part de l'air de norme F = f x'. La bobine a une résistance R et une inductance L. A. Détermination des équations mécanique et électrique. 51. Quelle force supplémentaire FL s'exerce lorsque la bobine est traversée par un courant i ? Indiquer le sens de cette force selon i. Une bobine parcourue par un courant et placée dans un champ magnétique est soumise à une force de Laplace. Cette force est dirigée selon Ox, dans le sens des x positif si le courant i a le sens indiqué sur la figure. 52. Donner l'expression de cette force. 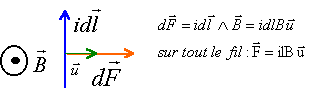l étant la longueur totale du fil. 53. Appliquer le second principe de la dynamique à l'ensemble mobile. L'origine de l'axe Ox est à la position d'équilibre lorsque la bobine est parcourue par un courant. Le système est soumis à son poids, à l'action du système de guidage, à la force de rappel exercée par le ressort, à la force de frottement et à la force de Laplace. La seconde loi de Newton s'écrit suivant Ox : m x" = -kx -fx' -ilB. m x" + kx + fx' =- ilB ( équation mécanique EM du système). 54. Lors de son utilisation, une force électromotrice e(t) apparaît dans la bobine. Sur un élément dl de la bobine, la fem de = B x' dl est induite. Intégrer le long de la bobine, dans le sens de i : e = B l x'. Appliquer la loi des mailles : u -R i -Ldi/dt + e=0. ( équation électrique EE du circuit. avec Ldi/dt, fem d'auto-induction ; Ri, tension aux bornes de la résistance ( déperdition par effet Joule). En régime sinusoïdal forcé : les grandeurs soulignées sont des nombres complexes associées aux ghrandeurs physiques. Pour l'équation électrique : u - Ri -jLw i + j l w x B= 0. Pour l'équation mécanique :- m w2 x + k x + f j w x = - i l B. On élimine x par substitution : x = (- u + Ri +jLw i ) / ( j l w B). Repport dans l'équation mécanique : (-m w2  + k + f j w )(- u + Ri +jLw i ) / ( j l w B)= -  i l B. Regrouper les termes : u . (m w2  - k - f j w ) = i [ (m w2  - k - f j w )( R + j Lw) - jwB2 l2 ]. Z = - jwB2 l2  / (m w2  - k - f j w ) + ( R + j Lw) On pose w0 = (k / m) et x = w / w0. Les courbes RT(x) et XT(x) pour le haut parleur étudié avec R = 6 ohms et L = 0,285 mH sont d'allure suivante. 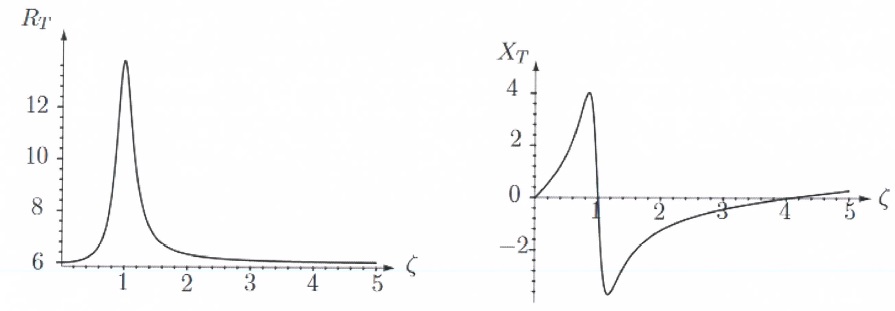66. A partir de ce document, calculer le module et l'argument de Z  pour w = w0, w = 2 w0 et w = 0,6 w0. pulsation ( rad/s) w = w0 w = 2 w0 w = 0,6 w0 RT (ohms) 14 0,87 1,2 XT(ohms) 4 -1,1 2 module de Z : (RT2 +XT2)½. 14,6 1,4 2,3 argument de Z ( rad) : cos F = RT / Z 0,29 -0,90 1,03 67. Justifier les valeurs de RT en hautes et basses fréquences. En hautes fréquences, la bobine se comporte comme un interrupteur ouvert. En basses fréquences, la bobine se comporte comme un interrupteur fermé. 68. Justifier la valeur de la résonance pour RT. 69. Calculer la valeur de la fréquence de résonance pour ce haut-parleur.

menu