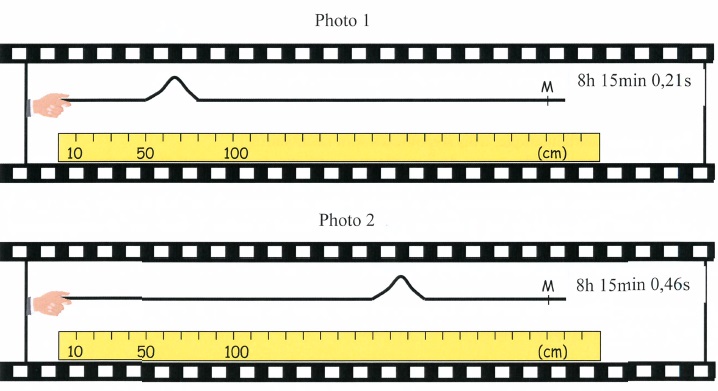
Onde sur une corde, Concours ITPE ingénieur  2018. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . I. Introduction.  On commence par l'expérience suivante, le point M étant libre. 1. Qualifier l'onde. Onde mécanique progressive transversale. 2. Déterminer la célérité de l'onde. L'onde parcourt 1,8 -0,5 = 1,3 m en 0,46-0,21 = 0,25 s. Célérité : c = 1,3 / 0,25 = 5,2 m / s. 3. A quelle date le point M se soulève t-il ? 1,8 / 5,2 = 0,346 s ~0,35 s ; 8 h 15 min 0,56 s. 4. Quelle est la durée du signal ? 0,3 / 5,2 = 0,0577 s ~ 0,058 s. 5. Le point M est fixé, que se passe t-il ? L'onde se réfléchit en M; la déformation, le signal, se produit vers le bas, le point M étant fixe. II. Etude de la corde de guitare. A Etude mécanique de la corde vibrante. On continue par l'expérience de la corde de Melde. Cette corde est supposée inextensible, de longueur L, de masse linéïque µ. Elle est tendue à la tension T à l'aide d'une masse accrochée à la corde via une poulie parfaite et excitée par un vibreur de mouvement vertical a  cos (wt) à son autre extrémité. 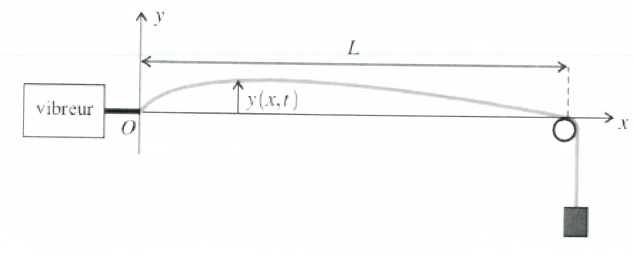On appellle y(x, t) le déplacement trannsversal d'un morceau de la corde de Melde situé en x à l'instant t. Trois hypothèses sont nécessaires :  - On néglige le déplacement  de la corde suivant l'axe des x, tant et si bien qu'un point de la corde situé en (x , 0 ) à l'équilibre se retrouve en (x, y(x, t) ) lors  de la vibration de la corde. - On suppose le déplacement de la corde faible de manière à ce que l'angle a(x,t) de la corde avec l'horizontale est faible et donc on se limite à l'ordre un dans les développements limités en cet infiniment petit. - On néglige le poids du fil devant sa tension. 6. On considère l'élément de corde de longueur dl situé entre les plans x et x +dx. Montrer que  lorsque la corde  est en mouvement dl ~dx. MM' = dl =[ (dx)2 + (dy)2 ]½= dx[ 1 + (dy / dx)2]½~ dx au premier ordre. a(x, t). étant petit, cos a(x, t)~1. 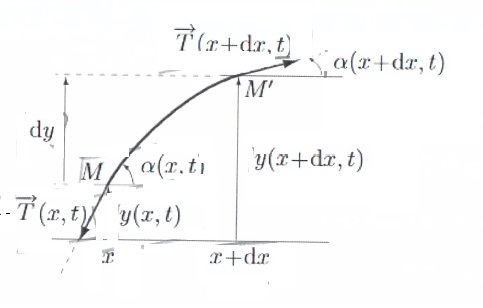. 7. Indiquer la signification des  différents termes représentés sur le schéma. MM' : élément de corde ; T(x+dx,t) et T(x, t)  : tension respectivement en M' et M. x et x+dx : abscisses respectives de M et M'. y(x, t) et y(x+dx, t) : ordonnées respectives de M et M'. a(x,t)  et a(x+dx,t)  angles de la corde avec l'horizontale. 8 à 11 Appliquer le principe fondamental de la dynamique à l'élément de corde MM' de masse dm et en déduire l'équation d'onde. L'élément  de corde MM' se meut sous l'action des forces de  tension tangentes à la corde aux points d'abscisses x  et x +dx. Le poids reste négligeable devant ces forces. On projette la relation fondamentale de la dynamique sur les axes Ox et Oy. 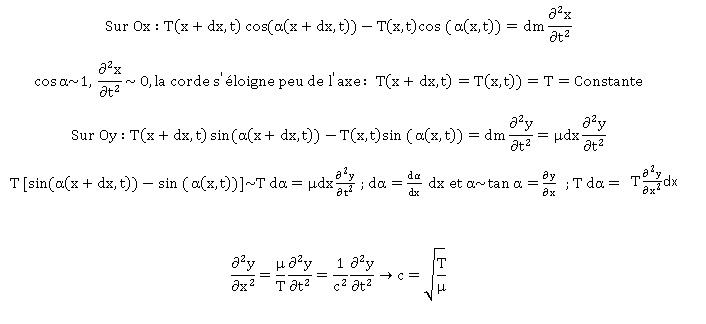12. Vérifier l'homogénéité de l'exppression obtenue pour c. T est une force exprimée en newton soit kg m s-2 ; µ est une masse linéïque, elle s'exprime en kg m-1. F / µ s'exprime en m2 s-2 ; c s'exprime bien en m s-1. 13. Calculer c pour µ= 3 g / m et T = 103 N. c =(103 /  (3 10-3))½ =185 m /s. B. Etude de la corde en résonance. 14. En variant la fréquence du vibreur, on observe parfois un mouvement de la corde d'amplitude très supérieur à celle du vibreur. Quel est ce phénomène ? On observe un phénomène de résonance loorsque la fréquence du vibreur est proche de la fréquence propre de la corde. 15. Expliquer en quelques lignes la cause de ces grands mouvement de la corde. Un système résonnant peut accumuler de l'énergie, si celle-ci est sous forme périodique et proche de la fréquence dite de "résonance". Le système est alors le siège d'oscillations importantes. Un équilibre est atteint ; cet équilibre dépend des éléments dissipatifs du système. Dans certains cas, un élément du système peut se rompre. 16. Définir le terme onde stationnaire. Lorsqu'une onde rencontre un obstacle rigide, elle produit une onde réfléchie ; la superposition d'une onde progressive sinusoïdale de fréquence f et de l'onde réfléchie sur un obstacle fixe produit une onde stationnaire : une vibration sans propagation, de fréquence f. 17. A quelle condition une variable du type y(x,t) = f(x) .g(t) peut elle être solution de l'équation d'onde ? f(x) doit être une fonction de x seul. C'est l'enveloppe. g(x) doit être une fonction du temps seul. C'est la pulsation. 18. En supposant f(x) =  A cos (kx +Y) et g(x) = B cos ( wt+j), nommer k et w. 19. Quelle relation est imposée sur k et w pour que y(x,t) =f(x) .g(t) soit solution de l'équation d'onde? w est une pulsation en rad / s ; k est la norme du vecteur d'onde ; k = w / c où c est la célérité de l'onde. 20. Définir les modes propres  et les fréquence propres de la corde. Un mode propre d'un système est une façon d'osciller lorsqu'il est abandonné à lui même. La fréquence propre d'un système est la fréquence à laquelle il oscille librement ( sans force excitatrice extérieure et sans force dissipative) . 21. Quelles sont les conditions aux limites sur la corde dans l'expérience ? f(0,t) = AB cos (Y). cos ( wt+j)=0, soit cos (Y) = 0 ; on choisit Y = - p / 2. f(x) =  A cos (kx +Y-p/2) = A sin (kx). f(L) =AB sin(kL) cos ( wt+j) = 0, soit kL = n p. ( n entier strictement positif ). 22. Montrer que les fréquences propres sont fn = n c / (2L), avec n entier naturel. k = n p / L = w / c = 2 p fn / c ; fn = n c / (2L). 23. Donner les longueurs d'ondes correspondantes. ln = c / fn = 2L / n. 24. Définir les ventres et les noeuds de vibration. Exprimer en fonction de la longueur d'onde l, les distances d1, d2 et d3 suivantes : d1 entre deux ventres consécutifs ; d2 entre deux noeuds consécutifs ; d3 entre un ventre et un noeud consécutifs. A un noeud, l'amplitude est nulle ( point immobile) ; à un ventre, l'amplitude est maximale. d1 = d2 = 0,5 l ; d3 = l / 4. 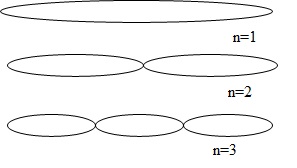25. Dessiner l'allure de la corde à différents instants pour n = 1, n = 2, n = 3. 26. Proposer une expérience permettant de mesurer les fréquences propres d'une corde. Dans l'expérience de la corde de Melde, la fréquence du vibreur est réglée à l'aide d'un GBF. Faire varier la fréquence du GBF jusqu'à obtenir un seul fuseau ample entre O et la poulie. 27. La corde précédente permet de jouer une note de fréquence fondamentale 147 Hz ( ré2). Quelle est sa longueur ? fn = n c / (2L) avec n = 1. 2L = c / f1 =185 / 147 ~ 1,26 ; L = 1,26 / 2 ~0,630 m. 28. Comment obtenir un ré3 ( 284 Hz) avec cette corde de guitare ? La fréquence double, la longueur de la corde est divisée par 2. Il faut pincer la corde en son milieu. C. Analyse fréquencielle. Le mouvement le plus général de la corde est obtenu par la superposition linéaire de ses modes propres, soit : 29. Comment appelle-t-on ce type de fonction mathématique ? Développement en série de Fourier. 30. Justifier que Fn = 0 pour tout n. Les conditions initiales imposent : vitesse initiale nulle : dy /dt = 0. La dérivée par rapport au temps de cos (npc / L t + Fn) est -npc / L sin (npc / L t + Fn). Une vitesse initiale nulle impose Fn=0. y(x,0) = 0 impose Yn =0. 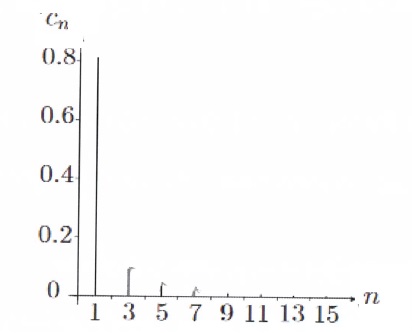On donne le spectre calculé pour une corde pincée à la moitié de sa longueur. 31. A quoi correspondennt l'abscisse et l'ordonnée ? Donner une unité possible pour chaque axe. Les fréquences en centaines de hertz sont reportées en abscisses. En ordonnée, on repporte les amplitudes acoustiques.. 32. Désigner et donner les valeurs de n correspondant au fondamental et aux harmoniques. n = 1 fondamental ; n = 3, 5, 7, 9 : harmoniques. 33. Justifier les valeurs de cn pour n pair. La fonction y(x,t) étant impaire, Cn =0 pour n pair. 34. Donner l'expression de y(x,t) en se limitant aux trois premiers termes. D'après le spectre C1 = 0,8, C3 = 0,12 et C5 = 0,05. y(x,t) = 0,8sin (px / L) cos ( p c t /L) +0,12 sin (3px / L) cos ( 3p c t /L) +0,05 sin (5px / L) cos ( 5p c t /L) 35. Le spectre de l'onde sonore est différent de celui proposé. Donner deux raisons à ces différences. On a pas tenu compte des effets dissipatifs ( pertes d'énergie dans la corde et au contact de l'air.

menu