Acoustique,
concours Geipi Polytech 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Un
guitariste ( en A) joue sans amplification sur une scène. Un ingénieur
du son est situé à 10 m de A. Il mesure un niveau d'intensité
acoustique LA = 67 dB. On considère le guitariste comme une source ponctuelle de bruit. L'intensité acoustique eput alors s'écrire :
IA (r) = WA / S(r) avec S(r) = 4 p r2 l'aire de la sphère de rayon r et de centre A.
Le niveau d'intensité acoustique s'écrit alors :
LA = 10 log( IA(r) / I0) avec I0 = 10-12 W m-2.
1. Quelles sont les unités de IA et WA ?
IA s'exprime en W m-2 et WA en watt.
2. Calculer littérallement LA(r' = 2r) en fonction de LA(r).
I'A (r) = WA / S'(r) avec S'(r) = 4 p(2r)2 .
I'A (r) =IA (r) / 4.
LA(r' = 2r)= 10 log [IA (r) / (4 I0)] = 10 log [IA (r) / I0] + 10 log (1 / 4) = LA(r) - 10 log 4 = 67 -6,0 = 61 dB.
3. En se plaçant à 40 m du guitariste, quel est le niveau d'intensité acoustique mesuré en dB ?
I'A (4r) =IA (r) / 16.
LA(r' = 4r)= 10 log [IA (r) / (16 I0)] = 10 log [IA (r) / I0] + 10 log (1 / 16) = LA(r) - 10 log 16 = 67 -12 = 55 dB.
L'intensité acoustique du guitariste sans amplification est trop faible
pour un concert en plein air. On décide de recourir à une
amplification. Deux ensembles d'enceintes sont placés en E et F.
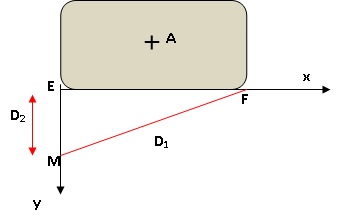
Les enceintes sont alimentées par un seul amplificateur, on considère
que ces enceintes sont les seules sources de son et qu'elles sont en
phase et cohérentes l'une avec l'autre.
|
|
4.
Lors d'essais avec un son pur, l'ingénieur M observe qu'en s'éloignant
de la scène ( direction Ey), le son fluctue en intensité. Quel
phénomène est à l'origine de cette fluctuation ?
Les ondes sonores émises par les deux enceintes ( sources cohérentes et synchrones) se superposent en M.
On observe un phénomène d'interférences.
Soit la relation entre la différence de chemin parcouru d = D2-D1 et la longueur d'onde l du son en un point de maximum ou de minimum d'intensité acoustique : d = n l / 2.
5. Que peut-on dire de n en un point d'intensité maximale ?
Les interférences sont constructives : n = 2k ; d = kl avec k entier relatif.
6. Que peut-on dire de n en un point d'intensité minimale ?
Les interférences sont destructives : n = 2k+1 ; d = (2k+1)l / 2 avec k entier relatif.
En s'éloignant de la scène, des points de maximas et de minimas
d'intensité sont perçus. On mesure pour chacun de ces points les
distances D1 ( en m) et D2 ( en m).
Intensité du son
|
D1
|
D2
|
D2-D1
|
minimum
|
127,5
|
129,30
|
1,55
|
maximum
|
62,71
|
65,82
|
3,11
|
minimum
|
40,51
|
45,18
|
4,67
|
maximum
|
29,02
|
35,24
|
6,22
|
minimum
|
21,81
|
29,60
|
7,78
|
7. Quelle est la longueur d'onde du son utilisé pour cette série de mesures.
Maximum : D2-D1 est égal à k l.
3,11 = k l. Pour k = 1, l = 3,11 m.
Minimum : D2-D1 est égal à (2 k+1) / 2 l.
Pour k = 0 : 1,55 = 0,5 l, l = 3,11 m.
|
|
8.
Sachant que la température extérieure était de 20 °C ( 293 K) au moment
des mesures et que la vitesse du son v ( en m /s) est v = 20 x T½, calculer la fréquence f1 du son pur utilisé pour ces essais.
v = 20 x293½ =342,3 m / s.
f1 = v / l = 342,3 / 3,11 ~110 Hz.
9. On utilise un
son pur de fréquence deux fois plus élevée. Le point de coordonnées ( 0
; 127,75 m) correspond à un maximum d'intensité, à un minimum
d'intensité ou aucun des deux ?
l =342,3 / 220 = 1,55 m.
D1 = 127,5 m ; D2 = 129,30 m ; D2-D1 = 1,55 m
D2-D1 = l, donc maximum d'intensité.
10. Si on utilise une guitare, plutôt qu'un son pur pour créer une note de fréquence fondamentale f1, quelle sera la sensation sonore au point M de coordonnées (0 ; 21,81 m ) ?
Cocher la ou les réponses exactes.
Le timbre de la guitare sera perturbé. Vrai, certaines harmoniques seront absentes.
La hauteur du son de la guitare sera perturbé. Faux, la hauteur reste égale à f1.
Le minimum sera moins marqué qu'avec un son pur. Vrai.
Le minimum sera plus marqué qu'avec un son pur. Faux.
Aucun changement. Faux.
l = v / f1 = 342,3 / 110 = 3,11 m.
(D2-D1) / l = 7,78 / 3,11 =2,5, donc minimum pour la fréquence fondamentale.
Pour la première harmonique de fréquence 2f1 : longueur d'onde = 1,55 m ; (D2-D1) / l = 7,78 / 1,55 =5 donc maximum.
Pour la seconde harmonique de fréquence 3f1 : longueur d'onde = 1,04 m ; (D2-D1) / l = 7,78 / 1,04 =7,5 donc minimum.
|
|