Suites,
probabilités, concours Geipi Polytech 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Suites.
Partie A.
a est un nombre réel. On considère la suite (vn) définie par, avec n entier :
v0 = a ; vn = -1 +n vn-1 avec n > 1.
1. Afin de calculer vn pour une valeur de n et de a données, on écrit l'algorithme suivant. Compléter la ligne 10.
1. Variables
2 k et n sont entiers
3 a et v sont des réels
4 Entrée
5 Lire la valeur de a
6 Lire la valeur de n
7 Traitement
8 v prend la valeur a
9 Pour k allant de 1 à n faire
10 v prend la valeur -1+k x v
11 Fin du pour
12 Sortir
13 afficher v.
Partie B
Pour tout entier naturel n, on considère la fonction fn définie par :
pour tout réel x , fn(x) = (1-x)n ex.
On considère les suites (un) et (In) avec n entier naturel, définies ci-dessous.
1. Donner la valeur exacte de u0 puis une valeur décimale approchée à 10-2 près.
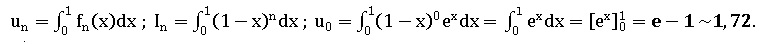
2. On considère la fonction F définie par F(x) = (2-x)ex, pour tout x réel.
2.a La dérivée F'(x) s'écrit sous la forme F'(x) = h(x) ex. Donner l'expression de h(x).
On pose u = 2-x et v = ex ; u' = -1 ; v' = ex.
F'(x) = u'v +v'u = -ex+(2-x)ex = (1-x)ex. h(x) = 1-x.
2.b. En déduire la valeur exacte de u1 en détaillant les calculs.
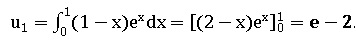
3. Exprimer In en fonction de n en détaillant les calculs.
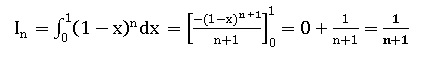
4.a. Donner un encadrement de ex lorsque 0 < x < 1 en justifiant.
e0 = 1 ; l'exponentielle est une fonction croissante : 1 < ex < e.
4.b. Montrer que pour tout n > 0, aIn < un < ßIn, où a et ß sont des réels strictement positifs à préciser.
1 < ex < e ; or, pour x appartenant à [0 ; 1 }, (1-x)n est positif.
1/ (n+1) < ex / (n+1) < e / (n+1).
(1-x)n < (1-x)n ex < (1-x)n e .
Par intégration entre 0 et 1 : In < un < e In. a = 1 et ß=e.
5. Justifier que un tend vers zéro si n tend vers plus l'infini.
In = 1 / (1+n) et e In tendent vers zéro quand n tend vers plus l'infini.
D'après le théorème des gendarmes, un tend vers zéro quand n tend vers plus l'infini.
Partie C.
Dans cette question n est un entier naturel non nul et x est un réel.
1.a. f 'n est la dérivée de fn. Détailler le calcul de f 'n.
On pose u = (1-x)n et v=ex : u' = -n(1-x)n-1 et v' = ex.
u'v+v'u = -n(1-x)n-1 ex+(1-x)n ex= (1-x)n-1 ex(1-n-x).
1.b. Donner
l'expression de fn(x)-f 'n(x) en fonction de fn-1(x).
fn-1(x) = (1-x)n-1 ex.
f 'n (x) =(1-n-x) fn-1(x) ;
fn(x)-f 'n(x) = (1-x) (1-x)n-1 ex-(1-n-x) fn-1(x) = n fn-1(x).
2. En déduire que pour tout n > 1, un = -1+n un-1.
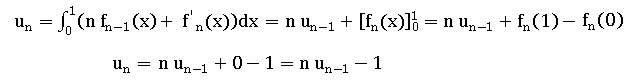
3. On admet le résultat suivant : pour tout n > 0, vn-un > n(v0-u0). Peut-on utiliser l'algorithme de la partie A avec a = 1,72 pour calculer une valeur approchée de un ? Justifier.
Non.
vn >n(v0-u0) +un.
Quand n tend vers plus l'infini un tend vers zéro.
v0-u0 >0 ; quand n tend vers plus l'infini vn tend vers plus l'infini.
|
|
|
Probabilités.
Un
équipementier de matériel sportif possède plusieurs magasins à la
montagne Il propose du matériel de glisse en location. La probabilité
que ce matériel soit abimé après une journée de location est p1 = 0,1 pour une paire de skis et p2 = 0,2 pour un surf.
Partie A.
Un sportif prénomé Julien loue du matériel durant toute la saison. A
chaque location, la probabilité qu'il loue des skis est égale à 0,7 et
celle qu'il loue un surf est égale à 0,3. On considère les événements
suivants :
A : " Julien rend le matériel abimé".
S : "Julien choisi de louer les skis".
B : " Julien rend le matériel en bon état".
1. Compléter l'arbre ci-dessous.
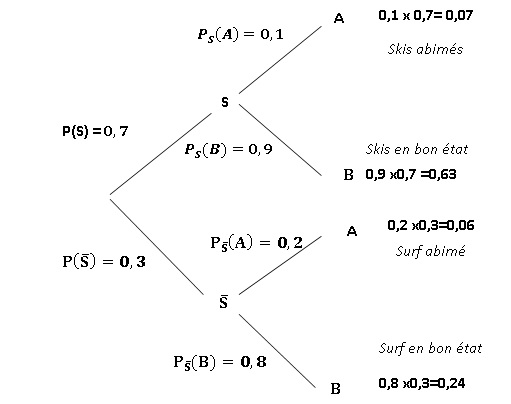
2. Indiquer si les affirmations suivantes sont vraies ou fausses..
2.a. La probabilité que Julien rende un surf abimé est supérieure à celle qu'il rende des skis abimés. Faux.
2.b. la probabilité que Julien rende le matériel en bon état est 0,7 p1 +0,3 p2. Faux.
0,7 (1-p1 )+0,3 (1-p2) = 1-0,7 p1 -0,3 p2.
2.c. Julien rend le matériel abimé. La probabilité qu'il s'agisse de skis est 7 / 13. Vrai.
0,07 / (0,06 +0,07) = 0,07 / 0,13 = 7 / 13.
.
|
|
|
|
|
Partie B.
L'équipementier fait payer 5 € la réparation du matériel loué à la
journée et rendu abimé. Julien compte effectuer n journées de location
de skis. On note X la variable aléatoire égale au nombre de locations
où il abime le matériel.
1. X suit une loi binomiale de paramètres n et p. Justifier que p = 0,13.
Probabilité que les skis soient abimés : 0,07.
Probabilité que le surf soit abimé : 0,06.
Probabilité que le matériel soit abimé : 0,06 +0,07 = 0,13.
2. Donner en fonction de n la probabilité p3 que Julien n'abime jamais le matériel pendant n journée.
p3 = 0,87n.
3. On note Mn le montant en euros, que Julien devra débourser en moyenne pour les réparations pendant la saison. Exprimer Mn en fonction de n.
Mn = 0,13 x n x 5= 0,65 n.
4.a. L'équipementier propose
aux clients réguliers de souscrire une assurance de 10 € qui couvre
toutes les réparations pendant la saison.
Julien a-t-il intérêt à souscrire l'assurance s'il loue 12 fois le matériel ?
0,65 x12 = 7,8 €. Réponse : non.
4.b. A partir de combien de locations la souscription de l'assurance est-elle rentable ?
0,65 n > 10 ; n > 10 / 0,65 ; n >15,38 ; n > 16.
Partie C.
L'équipementier affirme que 10 % des paires de skis loués à la journée sont rendus abimés.
Une
association sportive veut louer du matériel pour une journée.
L'équipementier prépare un lot de 85 paires de skis choisis au hasard
dans le stock. Soit F la variable aléatoire représentant la fréquence
de paires de skis rendues abimés dans le lot. On admet que F suit une
loi normale.
1. Donner un intervalle de fluctuation asymptotique I au seuil de 95% de F.
n = 85 > 20 ; np = 85 x0,1 = 8,5 >5 ; n(1-p) = 85x0,9 = 76,5 > 5.
Les conditions sont requises pour établir un intervalle de fluctuation asymptotique.
1,96 ((p(1-p) / n)½ =1,96 (0,1 x0,9 / 85)½ ~0,064.
I = [0,1-0,064 ; 0,1 +0,064] soit [0,036 ; 0,164 ]
2.
L'équipementier constate que 11 paires de skis sont rendues abimées.
Peu-on dire au seuil de risque de 5 % que la fréquence des paires de
skis rendues abiùées dans le lot confirme l'affirmation de
l'équipementier. Justifier.
11 / 85 = 0,129, cette valeur appartient à I. L'équipementier a raison..
|
|
|