Physique,
Concours technicien Douanes
2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Question 10
Le condensateur de la figure ci-dessous, de capacité
C, est initialement chargé sous une tension U0. A l’instant t=0, on
ferme l’interrupteur K.
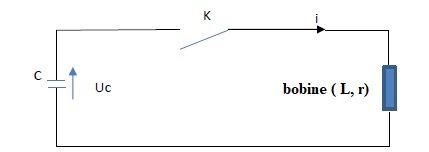
1. Etablir l’équation différentielle à laquelle obéit la tension Uc(t) aux bornes du condensateur.
Additivité des tensions : Uc = r i +Ldi/dt avec i = -dQ /dt = -CdUc/dt.
Uc =-rCdUc/dt -LC d2Uc/ dt2.
d2Uc/ dt2 + r / LdUc/dt +1/(LC) Uc = 0.
On suppose que la résistance r de la bobine est nulle.
2. Que devient dans ce cas l’équation différentielle ?
d2Uc/ dt2 +1/(LC) Uc = 0.
3. Donner une solution de cette équation différentielle qui vérifie la condition initiale sur Uc.
On pose w02 = 1 / LC ; Uc = A cos ( w0t + F).
Uc(t=0)= U0 = A cos (F) ; A = U0 et F = 0.
Uc = U0 cos ( w0t )
4. Donner l’expression générale de l’énergie stockée dans le condensateur, et de celle emmagasinée dans la bobine.
Energie stockée dans le condensateur : ½CUc2.
Energie stockée dans la bobine : ½Li2.
5. Quelle est l’expression de l’intensité maximale Im du courant circulant dans le circuit en fonction de C, L et U0.
Conservation de l'énergie : ½CU02= ½LIm2.
Im = (C / L)½U0.
6. Exprimer puis calculer la pulsation propre ω0 des oscillations, leur fréquence propre f0, et enfin leur période propre T0.
f0 = w0 / (2p) = 1 / ((LC)½ 2p).
T0 = 1 / f0 =2p (LC )½.
.
|
...
|
....
|
Question 11.
Un camion roule à la vitesse constant v= 90 km.h-1 La route nationale
comporte des graviers que le camion projette vers l’arrière avec une
vitesse v0 = 23 m.s-1 dans le référentiel de la route, et avec un angle
α = 10° par rapport à l’horizontale. Une voiture suit le camion à la
même vitesse que celui-ci.
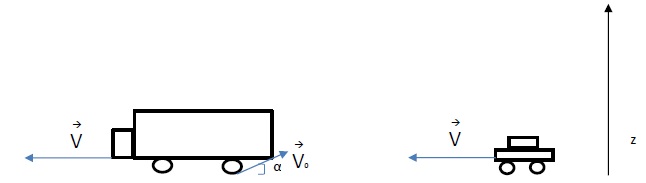
1. Etablir l’équation horaire du gravier dans le référentiel de la route. On négligera la résistance de l’air.
Le gravier est soumis uniquement à son poids.
L'axe horizontal est orienté vers la gauche. L'origine des temps et des
abscisses est choisie à l'instant où le gravier est projeté.
Composantes de l'accélération ( 0 ; -g).
Composantes de la vitesse du gravier :- v0 cos a ; v0 sin a -gt.
Coordonnées de position du gravier : x = - v0 cos a t ; y = -½gt2 + v0 sin a t.
2. Quelle est l’altitude maximale atteinte par le gravier ?
Lorsque l'altitude est maximale est atteinte, la composante verticale de la vitesse est nulle.
v0 sin a -gt = 0 ; t = v0 sin a /g.
ymax = -½g (v0 sin a /g)2 + (v0 sin a )2 / g = (v0 sin a )2 / (2g).
3. Etablir l’équation horaire du gravier dans le référentiel lié au camion.
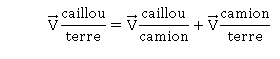
Composantes de la vitesse du gravier : -V- v0 cos a ; v0 sin a -gt.
Coordonnées de position du gravier : x = (-V- v0 cos a ) t ; y = -½gt2 + v0 sin a t.
4. On suppose que le camion est suivi à une distance d par une voiture
roulant à la même vitesse que lui. Quelle doit être la distance
minimale à laquelle se trouve la voiture, si on veut que le gravier
soit retombé sur la chaussée avant qu’il n’arrive au niveau de la
voiture ?
y = 0 ; -½gt + v0 sin a = 0 ; t = 2 v0 sin a / g.
x = -2 v02 sin a cos a / g = -v02 sin(2 a) / g.
d doit être supérieure à v02 sin(2 a) / g.
|
|