Physique,
école nationale supérieure maritime ENSM 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Question
1 . ( valeur 5 ).
Une source de lumière monochromatique S de longueur d'onde dans le vide l = 488 nm, éclaire deux fenntes étroites S1 et S2
séparées par une distance a = 0,20 mm et équidistantes de S. La figure
obtenue est observée sur un écran placé à la distance D = 1,00 m. La
différence de marche d entre les ondes provenant de S1 et S2 pour un point P d'abscisse x est donnée par d = ax / D.
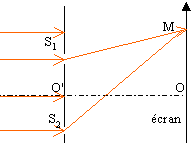
1. Donner le nom du phénomène observé lors de cette expérience.
Les sources S1 et S2, cohérentes et synchrones, diffractnte la lumière. Sur l'écran on observe des interférences.
2. Expliquer en quoi il est caractéristique des ondes. Donner le nom de deux autres phénomènes caractéristiques des ondes.
Les interférences, la diffraction; l'effet Doppler, sont caractéristiques des ondes.
3. Expliquer pourquoi la lumière n'est pas une onde mécanique.
La lumière se propage dans le vide, contrairement aux ondes mécaniques.
4. Montrer qu'au point O on observe une frange brillante.
En O, x = 0 et la différence de marche d est nulle. Lorsque la différence de marche est égale à un multiple de la longueur d'onde, les interférences sont constructives.
5. Calculer la différence de marche au point P telle que xP = 6,1 mm.
d = axp / D = 0,2 10-3 x 6,1 10-3 / 1,00 = 1,22 10-6 m = 1,22 µm.
6. Pour avoir une interférence constructive, la condition est d = kl ; pour avoir une interféreence destructive la condition est d = (k+0,5)l. Justifier ces conditions.
Si d = kl , les ondes sont en phase ; si d = (k+0,5)l les ondes sont en opposition de phase.
7. Montrer qu'au point P on observe une frange sombre.
xP / l = 1,22 / 0,488 = 2,5 ; d = (2+0,5)l.
Question 2 ( valeur 5).
Rutherfoord a décrit l'atome d'hydrogène par un modèle planétaire :
l'électron a un mouvement circulaire de rayon r autour du noyau
constitué d'un proton supposé fixe. La force électrostatique centripète
subie par l'électron a pour valeur Félec = ke2 / r2. la force gravitationnelle est négligeable devant la force électrique.
1. Représenter cette force et faire apparaître les vecteurs unitaires de la base locale de Frenet.
2. Donner l'expression de l'accélération de l'électron.
3. Montrer que le mouvement est uniforme.
4. Etablir l'expression de la valeur de la vitesse en fonction de k, e, m et r.
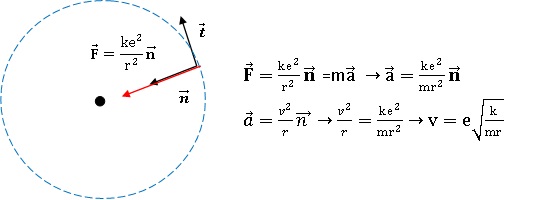
La force est constamment perpendiculaire à la vitesse : elle ne
travaille pas. L'énergie cinétique de l'électron reste constante : la
valeur de la vitesse est constante.
5. Etablir l'expression de l'énergie cinétique de l'électron en fonction de k, e et r.
Ec = ½mv2 =½ ke2 / r.
6. Exprimer son énergie mécanique en fonction de k, e, r et m sachant que son énergie potentielle est Ep = -ke2 / r.
E = ½ ke2 / r -ke2 / r = -½ke2 / r.
7. Montrer que l'énergie mécanique de l'électron est nulle lorsque r tend vers l'infini et que l'atome est ionisé.
Lorsqur r tend vers l'infini, E tend vers zéro. L'électron et le proton, ne sont plus liés : l'atome est ionisé.
|
|
|
Question 3. ( valeur 5)
On utilise un congélateur pour congeler 4,2 kg de nourriture de capacité thermique massique c = 3,2 103 J kg-1 K-1 avant congélation. Le processus de congélation comporte trois étapes :
étape 1 : abaissement à partir de la température ambiante de 20 °C jusqu'à 0+C.
étape 2 : changement d'état à la température constante de 0°C.
étape 3 : abaissement de la température jusqu'à -18°C.
1. Calculer l'énergie DU1 cédée par la nourriture lors de l'étape 1.
DU1 = mc (Tfin -Tdébut) = 4,2 x 3,2 103 (0-20) = -2,688 105 ~ -2,7 105 J.
2. Indiquer le mode de transfert prépondérannt de cette étape. Conduction.
3. Calculer l'énergie DU2 échangée lors de la congélation à 0°C sachant que la variation d'énnergie est de 200 kJ par kilogramme de nourriture.
DU2 = - 4,2 x 2,0 105 = -8,4 105 J.
Le congélateur permet d'abaisser la température de 0°C à -18°C. Pour cela il échange l'énergie DU3 =2,0 106 J avec la nourriture congelée.
4. Déterminer la capacité thermique massique de la nourriture congelée.
DU3 = mc' (Tfin -Tdébut) = 4,2 x c' (-18-0) = -2,0106 J.
c' = 2,0 106 /(4,2 x18)=2,645 104 ~2,6 104 J kg-1 K-1.
5.
Déterminer la durée nécessaire pour faire passer ces 4,2 kg de 20°C à
-18°C sachant que la puissance thermique utile du congélateur est P =
500 W.
| DU1 +DU2 +DU3 |=2,7 105 +8,4 105 +2,0 106 =3,11 106 J.
Durée = Energie / puissance = 3,11 106 / 500 ~6,2 103 s.
Le pouvoir de congélation en kg correspond à la masse d'aliments pouvant être congelée en 24 heures.
6. Déterminer le pouvoir de congéllation de ce congélateur.
4,2 / (6,2 103) x24 x3600 ~58 kg.
.
|
|
|
|
|
Question 4 . ( valeur 5).
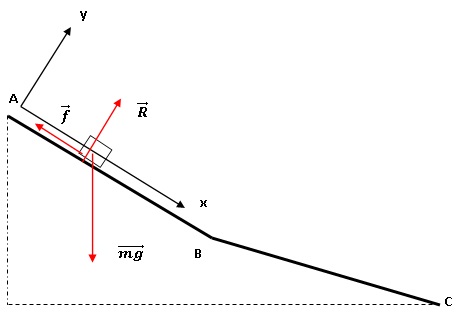
Un mobile S de masse m = 80,0 kg descend une piste constituée de deux parties AB et BC. On prendra g = 10 m s-2
. AB = 150 m est incliné de 20° par rapport à l'horizontal et le skieur
part de A sans vitesse. On néglige les forces de frottements.
1. Etablir les équations horaire du mouvement vx(t) et x(t).
Coordonnées de l'accélération : ( g sin 20 ; 0).
La vitesse est une primitive de l'accélération et la vitesse initiale est nulle : vx(t) = g sin 20 t = 10 sin 20 t.
La position est une primitive de la vitesse et l'abscisse initiale est nulle : x(t) = ½ 10 sin 20 t2 = 5 sin 20 t2.
2. Déterminer la durée du parcours AB et la vitesse en B.
t2 = 150 / (5 sin 20) = 87,7 ; t =9,36 s ~9,4 s.
vx = 10 sin 20 x 9,36 ~32 m s-1.
Les frottements ne sont plus négligés et sont modélisés par une force constante f = 200 N.
3. Etablir les équations horaire du mouvement vx(t) et x(t).
Coordonnées de l'accélération : ( g sin 15 -f / m; -g cos 20).
La vitesse est une primitive de l'accélération et la vitesse initiale est nulle : vx(t) = (g sin 20- 200 / 80,0) t = (10 sin 20-2,5) t.
La position est une primitive de la vitesse et l'abscisse initiale est nulle : x(t) = ½ (10 sin 20-2,5) t2 = (5 sin 20-1,25) t2.
4. Déterminer la durée du parcours AB et la vitesse en B.
t2 = 150 / (5 sin 20-1,25) = 326 ; t =9,36 s ~18 s.
vx = (10 sin 20-2,5) x 18 =16,56 ~17 m s-1.
La piste BC est inclinée de 10 ° par rapport à l'horizontale et le mobile possède en B une vitesse v0 qui reste constante entre B et C. Les frottements sont modélisés par une force constante f '.
5. Calculer f ' en utilisant les notions de travail et d'énergie.
L'énergie cinétique ne varie pas entre B et C. La somme des travaux des forces est nulle..
Travail moteur du poids : m g BC sin 10 ;
travail résistant des frottements : - f ' BC.
Par suite : f ' =mg sin 10 = f ' = 80 x10 x sin 10 ~139 N ~1,4 102 N.
|
|
|