Mathématiques,
école nationale supérieure maritime ENSM 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Question
1 .
1. On considère la fonction g définie sur R par g(x) = x3 -4x2 -x+2.
1.1. Calculer g'(x) et en déduire le tableau de variations de g. ( on ne cherchera pas à calculer les valeurs des extrémums de g)
g'(x) = 3x2-8x-1.
3x2-8x-1 = 0. Discriminant D = 64+12=76.
x1 = (8-2*19½) / 6 ~ -0,12 ; x2 = (8+2*19½) / 6 ~ 2,8 .
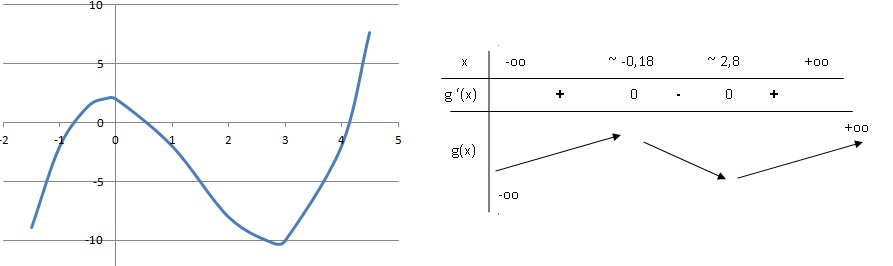
1.2. Démontrer que l'équation g(x)=0 admet une solution unique notée a sur l'intervalle [0 ; 2 ].
Sur cet intervalle, g(x) est strictement décroissante.
De plus f(0 ) = 2 et f(2 ) = -8.
L'équation g(x) = 0, admet donc une unique solution sur cet intervalle.
1.3. En déduire le tableau des signes de g(x) sur [0 ; 2 ].
g(x) > 0 sur [0 ; a[ ; g(x) < 0 sur ]a ; 2].
Pour la suite on prendra a ~0,64.
2. On considère la fonction f définie sur R par f(x) = (ax+b) exp(-x2) et on note C sa courbe représentative.
2.1 On sait que C coupe l'axe des ordonnées au point A (0 ; 4) et que sa tangente en A a pour coefficient directeur -1.
Démontrer que f(x) = (-x+4)exp(-x2).
f(0) = b exp(0) = b = 4.
Calcul de la dérivée en posant u = ax+4 et v = exp(-x2) ; u' = a ; v' = -2x exp(-x2).
u'v + v' u = a exp(-x2) -2x (ax+4) exp(-x2) = (a-2x(ax+4))exp(-x2).
f '(x) = (2x2-8x-1)exp(-x2) ; f '(0) = a = -1.
2.2. Pour tout réel x de l'intervalle [0 ; 2 ], on définit les points suivants :
M( x ; f(x) ; P(x ; 0) ; Q(0 ; f(x)) et on note A(x) l'aire du rectangle OPMQ.
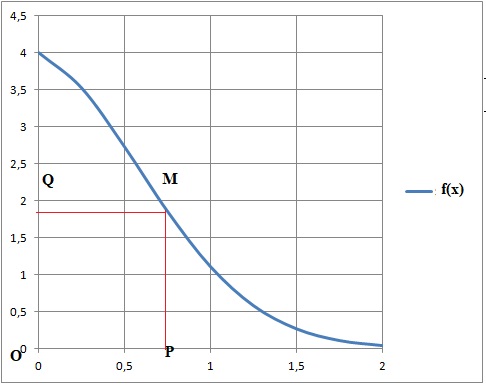
2.2.1 Exprimer A(x) en fonction de x.
A(x) = OP * OQ = x f(x).
2.2.2. Démontrer que A'(x) est du signe de g(x) et en déduire la valeur de x pour laquelle A(x) est maximale.
A'(x) = f(x) +x f '(x) = (-x+4)exp(-x2)+ x (2x2-8x-1)exp(-x2).
A'(x) =(2x3-8x2-2x+4 )exp(-x2) =2 g(x) exp(-x2).
Le terme en exponentielle étant positif, A'(x) est du signe de g(x).
g(x) > 0 sur [0 ; a[ ; A(x) est croissante sur cet intervalle.
g(x) < 0 sur ]a ; 2] ; A(x) est décroissante sur cet intervalle.
A (x) est maximale pour x = a.
2.2.3. Démontrer que lorsque A(x) est maximale, la tangente à Cf en M est parallèle à la droite QP.
Coefficient directeur de la droite (QP) : - f(a) / a = (1-4 / a )exp(-a2).
Coefficient directeur de la tangente à Cf en M : f '(a) = (2a2-8a-1)exp(-a2)
Or g(a) = a3 -4a2 -a+2 = 0 ; 0,5 a (2a2-8a) = a-2 ; (2a2-8a)= 2-4/a ;
(2a2-8a-1)=1-4/a ; f '(a) =(1-4 / a )exp(-a2).
La tangente en M à Cf et la droite QP ont le même coefficient directeur : elles sont parallèles.
3. On note S l'aire du domaine compris entre la courbe Cf, l'axe des abscisses, l'axe des ordonnées et la droite d'équation x = 2.
Calculer l'intégrale suivante et en déduire l'aire approchée de S à 10-2 près.
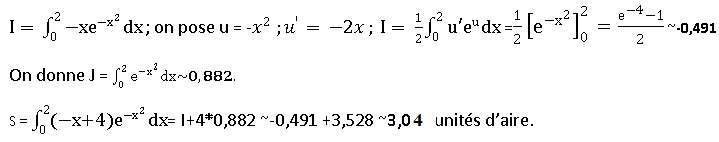
Est-il possible de placer le point M pour que l'aire du rectangle OPMQ soit égale à la moitié de l'aire S ?
A =x f(x) = (-x2+4x)exp(-x2) ; Amaxi = (-0,642 +4*0,64) exp(-0,642) ~2,15 *0,664 ~1,43, valeur inférieure à 0,5 S.
Réponse : non, c'est impossible.
|
|
|
Question 2.
Soit f la fonction définie sur ]-0,5 ; +oo[ par f(x) = 2x /(1+2x).
On considère la suite (un) définie par u0 = 2 et pour tout entier n, par un+1 = f(un).
1. Sur le graphique suivant, construire les points d'abscisses u0, u1, u2 et u3. ( aucun calcul n'est attendu ).
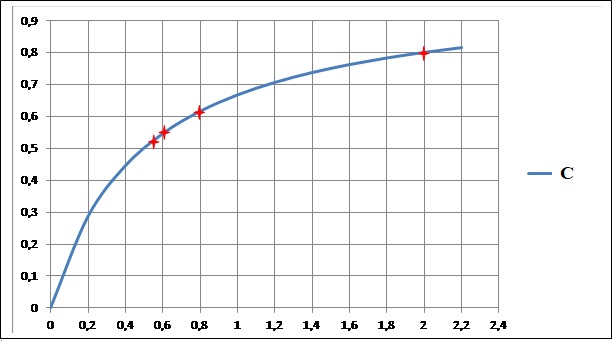
1.2. Quelles conjectures peut-on émettre sur le sens de variation et sur la convergence de la suite (un) ?
La suite est décroissante. La suite est minorée par 0,50.
2.1. Etudier les variations de la fonction f sur son ensemble de définition.
On pose u = 2x ; v = 2x+1 ; u' = 2 ; v' = 2 ; (u'v-v'u) / v2=(4x+2-4x) / (1+2x)2 = 2 /(1+2x)2.
La dérivée est positive ; f(x) est strictement croissante.
2.2. Démontrer par récurrence que pour tout entier n, 0,5 < un+1 < un.
Initialisation : u0 = 2 ; u1 = 0,8 , la propriété est vrai au rang zéro.
Hérédité : 0,5 < up+1 < up est supposée vrai.
f est croissante : f(up+1) < f(up) soit up+2 < up+1 .
Conclusion : la propriété est vraie au rang zéro et héréditaire, donc elle est vrai pour tout entier n.
2.3. En déduire que la suite converge.
La suite est décroissante et minorée par 0,5. Elle converge.
3. On considère la suite (vn) définie sur N par : pour tout entier naturel n, vn = (1-2un) / un
3.1. Démontrer que la suite (vn) est géométrique de raison 0,5.
vn = 1 / un -2 = 1 / f(un-1) -2 = (1+2un-1) / (2 un-1) -2 = (1-2un-1) / (2 un-1)= vn-1 / 2.
3.2. Déterminer l'expression de vn puis celle de un en fonction de n.
v0 = (1-2u0) / u0 =(1-4) / 2 = -1,5.
vn = -1,5 *0,5n ; un vn= 1-2un ; un=1 / (vn+2) =1 / (-1,5 *0,5n +2).
3.3 En déduire la limite de la suite (un).
Quand n tend vers plus l'infini, 0,5n tend vers zéro et un tend vers 1 / 2.
3.4 Déterminer le premier entier n0 tel que pour tout n > n0, un < 0,501.
1 / (-1,5 *0,5n +2) < 0,501 ; 1 < 0,501(-1,5 *0,5n +2) ;
1 < 1,002 -0,7515*0,5n ; 0,7515*0,5n < 0,002 ; 0,5n < 0,002 / 0,7515 ; 0,5n < 0,00266 ;
n ln(0,5) < ln (0,00266) ; n > 8,55 ; n0 = 9.
.
|
|
|
|
|
Question 3 .
Une
entreprise produit et commercialise des puces GPS. Elle dispose de
trois centres de production A, B et C qui produisent respectivement 60
%, 25% et 15 % de ces puces. L'expérience a montré que 85 % des puces
issues de A, 95 % des puces issues de B et 86,45 % des puces issues de
C sont commercialisables après un contrôle de qualité.
1. Un technicien prélève une puce au hasard pour lui faire passer le test. On note les événements suivants :
A : "la puce est issue de A", de même pour B et C.
T : " la puce est sélctionnée à l'issue du test comme étant commercialisable".
1.1. Décrire la situation par un arbre pondéré.
1.2. Calculer la probabilité que la puce provienne de A et soit commercialisable.
1.3. Calculer la probabilité que la puce provienne de C et soit commercialisable.
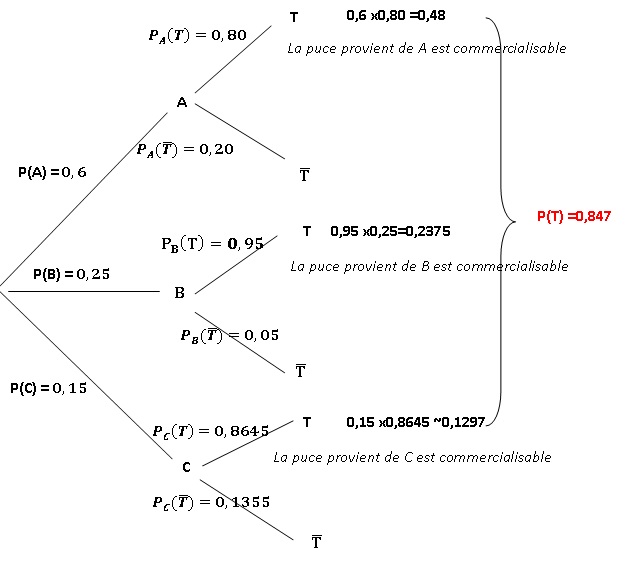
1.4. Le responsable
du centre de production C affirme que parmi les puces commercialisées,
plus de 17 % proviennent de son centre de production. Justifier cette
affirmation par un calcul de probabilité.
0,1297 / 0,847 =0,153 ( 15,3 %). Cette affirmation est fausse.
2. Pour faire les
tests, les techniciens reçoivent les puces par lots de 12. On note X la
variable aléatoire qui à un lot choisi au hasard associe le nombre de
puces commercialisables qu'il contient.
2.1. Donner la loi de probabilité que suit la variable X en justifiant.
Deux issues sont possibles : puce commercialisable ou puce non commercialisable.
Les tests sont indépendants.
X suit une loi binomiale de paramètre n = 12 et p =0,847.
2.2. Calculer la probabilité qu'au moins une puce du lot ne soit pas commercialisable.
"au moins une " signifie : 1 ou 2, ou 3.....ou 12 ne sont pas commercialisables.
Probabilité que les 12 puces soient commercialisables : P(X=12) = C1212 x0,84712 x(1-0,847)0 = 0,136.
P( X > 1)=1-0,136=0,864.
2.3 Calculer la
taille minimale des lots pour que la probabilité qu'un lot contienne au
moins une puce non commercialisable soit supérieur à 0,95.
Si n = 18 : P(X =18) =0,0503 ; P( X > 1)=1-0,0503=0,9497.
Si n = 19 : P(X =19) =0,0426 ; P( X > 1)=1-0,0426=0,954.
3. On estime que la durée de vie de ces puces suit une loi exponentielle de paramètre l et
on note T la variable aléatoire qui à une puce choisie au hasard
associe sa durée de vie en années. On a mesuré qu'au bout de 5 ans la
moitié des puces sont défectueuses.
3.1. Déterminer la valeur de l.
P(T > 5)= 0,5 = exp(-5l) ; -5 l = ln (0,5) ; l = 0,1386.
3.2. En déduire la durée de vie moyenne de ces puces.
1 / 0,1386 = 7,2 années.
3.3. Un bateau de
plaisance doit partir pour une croisière de 2 ans. Il est équipé d'un
dispositif qui utilise une de ces puces et qui a été acheté neuf il y a
4 ans. Qu'elle est la probabilité qu'il connaisse une panne durant
cette croisière ?
la loi exponentielle est sans mémoire.
P(T < 2) = 1 -exp(-0,1386 x2)=0,242.
|
|
Question 4.
1. On considère le polynôme P défini sur C par : P(z) = z3 +(2+2i)z2 +(4-4i)z -8i.
1.1. Démontrer que 2i est une solution de l'équation P(z) = 0.
P(2i) = (2i)3+(2-2i)(2i)2 +(4-4i)(2i) -8i.
P(2i) = -8 i -4(2-2i) +(4-4i)(2i) -8i.
P(2i) = -16 i-8 +8i +8i+8 = 0.
1.2. Démontrer que P(z) = (z-2i)(z2+2z+4).
P(z) = (z-2i)(z2 +az +b).
On développe : P(z) = z3 +az2 +bz -2iz2-2aiz-2ib.
P(z) =z3 +(a-2i)z2 +(b-2ai)z-2ib= z3 +(2+2i)z2 +(4-4i)z -8i.
On identifie : a = 2 ; b = 4.
1.3. En déduire toutes les solutions dans C de l'équation P(z) = 0.
z2+2z+4 = 0 ; discriminant D = 4-16 = -12 = 12 i2.
z1 = (-2 +2*3½i) / 2 = -1 +3½ i.
z2 = (-2 -2*3½i) / 2 = -1 -3½ i.
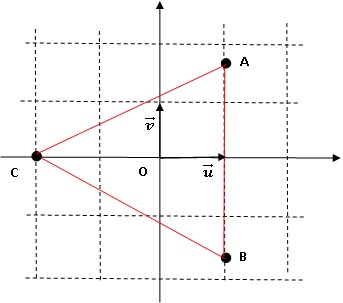
2. On considère les points A, B et C d'affixes respectives : zA =1+i3½ ; zB = 1-i 3½ et zC = -2.
2.1. Déterminer le module et l'argument de ces nombres puis les écrire sous forme exponentielle.
|zA| = (1+3)½ = 2 ; zA / |zA|=1 / 2 +i 3½ / 2 = cos (p/3) + i sin (p/3) ; zA = 2 exp(ip/3).
|zB| = (1+3)½ = 2 ; zB / |zB|=1 / 2 -i 3½ / 2 = cos (-p/3) + i sin (-p/3) ; zB = 2 exp(-ip/3).
|zC| = 2 ; zC = 2 exp(ip).
2.2. Placer les points sur une figure que l'on complètera au fur et à mesure de l'exercice.
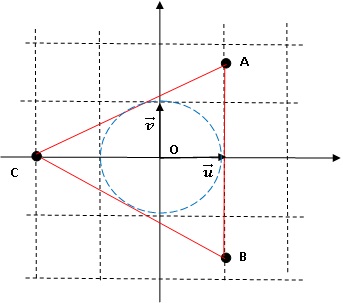
2.3. On note Z =( zA-zC) / (zB-zC). Déterminer la forme algébrique de Z ; calculer son module et son argument et en déduire la nature du triangle ABC.
zA-zC= 3 +i3½ ; zB-zC= 3 -i3½.
Z = (3+i3½) / (3-i3½)= (3+i3½)2 / (9 +3)=(9+3+6 i 3½) / 12 =0,5(1+ i 3½) = cos (p/3) + i sin (p/3) ;
|Z|=0,5(1+3)½ =1 ; Z = exp(ip/3).
Le triangle ABC est équilatéral.
3. A tout point M d'affixe z= a+ib ( avec z différent de zB), on associe le point M' d'affixe z' = (1+i 3½-z) / (1-i 3½-z)= (zA-z) / (zB-z).
3.1. Démontrer que
si le point M appartient à la médiatrice du segment [AB] alors M'
appartient à un cercle dont on précisera le centre et le rayon.
M est sur la médiatrice de [AB] ; M appartient à l'axe horizontal des nombres réels : affixe de M ; z = a.
MA=MB ; |zA-z| = |zB-z|. Le module de z' est égal à 1.
zA-z = (1-a)+i3½ ; zB-z = (1-a)-i3½ ;
|zA-z| =((1-a)2 +3]½ ; |zB-z| =((1-a)2 +3]½ ;
z' = [(1-a)+i3½] / [(1-a)-i3½] = [(1-a)+i3½]2 / [(1-a)2 +3] = [(1-a)2-3 +2i(1-a)3½] / [(1-a)2 +3] = x+i y.
On identifie partie réelle et partie imaginaire :
x=(1-a)2-3) /[(1-a)2 +3] ; y =2(1-a)3½ / [(1-a)2 +3].
x2 +y2 =1
M' appartient au cercle de centre (0 ; 0) et de rayon 1.
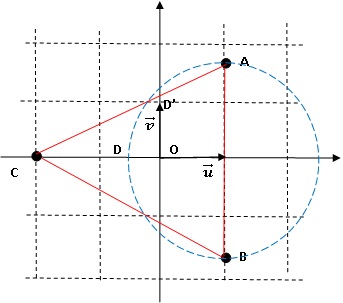
3.2. Démontrer que si M appartient au cercle de diamètre [AB] privé de B, alors M' appartient à l'axe vertical.
M est tel que (x-1)2 + y2 = 3 avec z = x+iy
zA-z = (1-x)+i(3½-y) ; zB-z = (1-x)-i(3½+y) ; z' =[(1-x)+i(3½-y)] / [(1-x)-i(3½ +y)] =[(1-x)+i(3½-y)] [(1-x)+i(3½ +y) ]/ [(1-x)2+(3½ +y)2] .
z' = [(1-x)2-(3-y2)+2i(1-x)(3½)]/ [(1-x)2+(3½ +y)2] ;
z' =2i(1-x)(3½)] / [(1-x)2+(3½ +y)2] ; z' est un imaginaire pur.
3.3. On note D le
point d'intersection entre le cercle de diamètre AB et l'axe réel, tel
que DBA soit un triangle rectangle direct. Construire le point D'
associé à D en justifiant la construction.
xD = - 3½+1 ; yD = 0 ; 1-x = 3½ ; z' = 6i /(3+3)= i.
|
|