Mathématiques, école nationale supérieure maritime ENSM 2016

Mathématiques, école nationale supérieure maritime ENSM 2016.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Question 1 ( 4 points).
Un volume constant de 2200 m³ d'eau est réparti entre deux bassins A et B. Une circulation est créée entre les bassins à l'aide d'un système de pompes. A a une capacité de 1200 m³ et contient initialement 800 m³ d'eau. Toutes les 24 heures, 15 % du volume d'eau présent en B est transféré vers A alors que 10 % du volume d'eau du bassin A est transféré vers B.
Pour tout entier n > 1 on pose :
a_n le volume d'eau en m³ contenu dans le bassin A après le n ième jour de fonctionnement.
b_n le volume d'eau en m³ contenu dans le bassin A après le n ième jour de fonctionnement.
On a donc a₁ = 800.
1.a. Par quelle égalité liant a_n et b_n, la conservation du volume d'eau se traduit-elle ?
a_n + b_n = 2200.
1.b. Justifier que pour tout entier n >1, on a : a_n+1 = 0,75 a_n +330.
a_n+1 = 0,9a_n+0,15 b_n = 0,9a₁+0,15 (2200-a_n) = 0,75 a_n+330
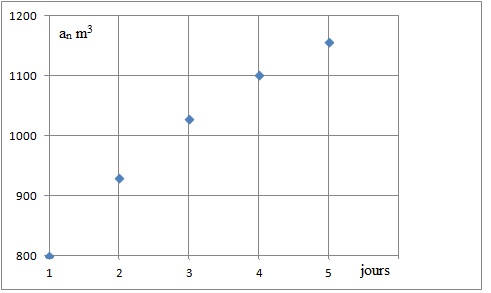
2.a. Le plan étant muni d'un repère orthogonal ( 1 cm représente 200 m³ ), on note D et D' les droites d'équations y = x et y = 0,75x +330. Représenter graphiquement les 5 premiers termes de la suite (a_n).

2.b. On note (u_n) la suite définie par u_n = a_n -1320 pour tout entier n >1.
Montrer que (u_n) est une suite géométrique. En déduire l'expression de a_n en fonction de n.
u_n+1=0,75 a_n +330-1320 = 0,75 a_n -990= 0,75 ( a_n -990 / 0,75) =0,75 ( a_n -1320) = 0,75 u_n.
(u_n) est une suite géométrique de raison 0,75 et de premier terme u₁ =800-1320= = -520.
a_n = u_n +1320= 1320-520x 0,75^n-1.
2.c. Au bout de combien de jours doit-on stopper la circulation d'eau pour éviter le débordement du bassin A ?
1320-520x 0,75^n-1< 1200 ; 120 < 520 x 0,75 ^n-1 ;
ln ( 120 / 520) < (n-1) ln (0,75) ; n-1 <5,1 ; n < 6.

Question 2. (5 points).
1. Montrer que l'équation (E) : x³=3x-1 admet trois solutions distinctes dans R comprises entre -2 et +2.
.
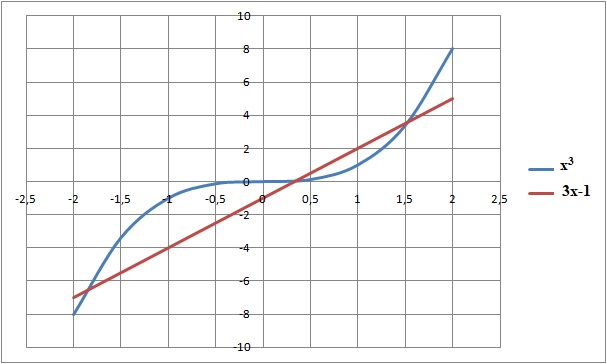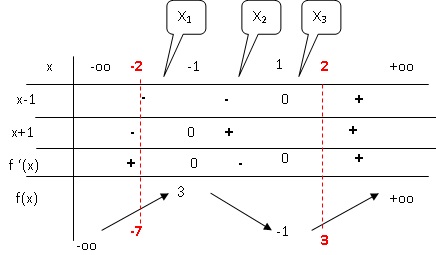
On pose f(x) =x³-3x+1.
f '(x) = 3x² -3=3(x²-1)=3(x+1)(x-1).

2.a. On se propose de déterminer les valeurs exactes de ces trois solutions. Déduire de l'égalité e^3it= (e^it)³ que :
cos(3t) = 4 cos³(t) -3cos(t) avec t réel.
e^3it= cos (3t) + i sin(3t) ; (e^it)³ = (cos(t) + i sin(t))³ = cos³(t) -i sin³(t) -3 cos(t) sin²(t)+3i cos²(t) sin(t).
On identifie les parties réelles : cos(3t) = cos³(t)-3 cos(t) sin²(t).
sin²(t) = 1 -cos²(t) ; cos(3t) = cos³(t)-3 cos(t)+3cos3(t).
2.b. Soit x l'une des solutions de (E). x étant compris entre -2 et 2, il existe un unique réel t appartenant à [0 ; p] tel que x = 2 cos(t).
En déduire que t appartenant à [0 ; p] est tel que : 1 +2cos(3t) = 0 ; déterminer les valeurs exactes de x₁, x₂ et x₃.
x³ -3x +1 = 0 ; 8 cos³(t) -6 cos(t) +1 = 0.
Or 4 cos³(t) =cos(3t) + 3cos(t) ; 2 cos(3t) + 6 cos(t) -6 cos(t) +1 = 0 ; 2 cos(3t)+1 = 0.
cos (3t) = -0,5 = cos (2p/3).
3t = 2p/3 + 2 kp ; t = 2p/9 + 2 kp /3 ; t = 2p/9 ; x₃ = 2 cos(2p/9) ~1,53.
t = 8p/9 ; x₁ = 2 cos(8p/9) ~-1,88.
t = -4p/9 ; x₂ = 2 cos(4p/9) ~ 0,347.

Question 3. ( 6 points).
La durée de vie d'un composant noté C a une durée de vie en semaines qui suit la loi exponentielle de paramètre l = 0,02.
1. Quelle est la durée de vie moyenne d'un composant ?
µ = 1 / l = 1 /0,02 = 50 semaines.
2. On monte deux composants C en parallèle. Le signal peut être transmis tant que l'un des composants est en état de marche. les durée de vie des composants sont indépendantes. On note :
T₁ la variable aléatoire mesurant la durée de vie en semaines du composant 1.
T₂ la variable aléatoire mesurant la durée de vie en semaines du composant 2.
T la variable aléatoire mesurant la durée de vie en semaines des composants montés en parallèle.
a. Déterminer en fonction de t ( réel positif exprimé en semaine), la probabilité que ce système cesse de fonctionner avant la date t.
P( T₁ < t) =1-e^-0,02t.
P( T₂ < t) =1-e^-0,02t.
T₁ et T₂ étant indépendants : P(T < t) = P(T₁ <t) n P(T₂ <t) = (1-e^-0,02t)(1-e^-0,02t) =(1-e^-0,02t)².
Le système tombe en panne si les deux composants sont défaillants.
Probabilité que le système cesse de fonctionner avant la date t : (1-e^-0,02t)².
b. On rappelle que la fonction de densité de probabilité, f, de la variable T, est la fonction numérique f telle que :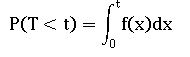
En déduire que la fonction de densité de probabilité f de ce système est f(x) = 0,04(e^-0,02x -e^-0,04x).
P( T < t)=(1-e^-0,02t)².
On dérive en posant u = 1-e^-0,02t ; u' =0,02e^-0,02t ; f(x) = 2 uu' =0,04e^-0,02t(1-e^-0,02t).
c. La durée de vie moyenne en semaine de ce système est le réel E(t) telle que :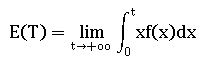
k désignant une constante réelle non nulle, montrer qu'une primitive sur [0 ; +oo[ de la fonction x e^kx est la fonction ( ax+b) e^kx où a et b sont deux constantes réelles dont vous donnerez l'expression en fonction de k.
Dériver ( ax+b) e^kx en posant u = ax+b et v = e^kx ; u' = a ; v' = k e^kx ; u'v+v'u = ae^kx+ (ax+b) k e^kx =(a+bk +akx)e^kx.
On identifie : ak = 1 ; a = 1 / k ; a+bk = 0 ; b= -a / k = -1 /k².
En déduire E(x).
x f(x) = 0,04 [ x e^-0,02x - xe^-0,04x].
Primitive de x f(x) : 0,04 [-1 / 0,02( x+1 / 0,02) e^-0,02x+1 / 0,04 ( x+1/ 0,04) e^-0,04x].
0,04 [-1 / 0,02( t+1 / 0,02) e^-0,02t+1 / 0,04 ( t+1/ 0,04) e^-0,04t] -0,04[-1 /0,02²+1 /0,04²].
2 [-1( t+1 / 0,02) e^-0,02t+ ( t+1/ 0,04) e^-0,04t] - [-2 /0,02+1 /0,04].

Quand t tend vers plus l'infini :
e^-0,02t tend vers zéro ; (t+1/k)e^kt tend vers zéro.
E(T) =2 / 0,02 -1 / 0,04 = 100-25 = 75.
Pourcentage d'augmentation : (75-50) / 50 x100 = 50 %.

Question 4 ( 5 points). Vrai ou faux avec justification.
1. Le plan complexe est muni d'un repère orthonormé direct. Pour tout n entier naturel, Mn désigne le point de ce plan dont l'affixe est définie par :
z₀ = 1 et z_n+1 =(1-i 3^½) z_n.
Affirmation 1 : Le triangle OM_nM_n+1 est un triangle rectangle. Vrai.
z₁ =1-i 3^½,M₁( 1 ; -3^½) ; OM₁² = (1+(-3^½)²) = 4.
z₂ =(1-i 3^½)²= -2 -2i 3^½ ;M₂( -2 ; -2 *3^½) ; OM₂² = (4+(-2*3^½)²) = 16 ;
M₁M₂ ²=( (-2-1)² +(-2 *3^½+3^½)²)^½ =12.
Angle formé entre OM_n et OM_n+1 : 60 °.
OM_n+1 / OM_n = 2. le triangle OM_nM_n+1 est un triangle demi-équilatéral.

Affirmation 2 : Il n'existe aucune valeur de n pour laquelle M_n est un point de l'axe vertical. Vrai.
On pose y =1-i 3^½ ; |y| = (1 +3)^½ = 2 ; y / |y| =0,5 -i 3^½ / 2 = e^-ip/3.
z_n+1 =2e^-ip/3z_n= 2ⁿ⁺¹ exp (- i(n+1)p /3) =2ⁿ⁺¹ ( cos ( (n+1)p /3))-i sin( (n+1)p /3))).
z_n+1 est un imaginaire pur si (n+1)p /3) =k p /2 avec k entier ; (n+1) / 3 = k / 2 ; n+1 = 1,5 k ; n = 1,5 k-1.

2. L'espace est muni d'un repère orthogonal. On considère les points A (-3 ; 1 ; 1) ; B(-1 ; -3 ; -1) et le plan P d'équation x-2y-z=0.
Affirmation 3 : B est le symétrique de A par rapport au plan P. Vrai.
Coordonées d'un vecteur normal au plan P : (1 ; -2 ; -1).
Coordonnées du vecteur AB : (-1-(-3) ; -3-1 ; -1-1) soit (2 ; -4 ; -2).
Ces deux vecteurs sont colinéaires.
Coordonnées du milieu I de AB : (-2 ; -1 ; 0).
Si I appartient au plan P : -2 -2(-1)-0 =0 est vérifié.

3. Lorsque 1 / e < x < e, l'expression ln(x) +1/x est majorée par e-1. Vrai.
On dérive f(x) = ln(x) +1/x ; f '(x)= 1 / x -1/x² = 1/x ( 1-1 /x), s'annule pour x = 1 ; f(1) = 1.
f '(x) est négative pour x appartenant à [1 / e ; 1] : f(x) est décroissante de ln(1/e)+e = e-1.
f '(x) est positive pour x appartenant à [1 ; e] : f(x) est croissante de 1 à ln(e) +1/e =1+1/e.

menu