Gravitation,
diffraction, pont de Wheastone, radar de recul,
concours EMIA
2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
1. La
station spatiale ISS.
On considère un point M en mouvement dans le plan (O, x, y) et une base
mobile centrée en M.
1. Déterminer
l'expression du vecteur vitesse dans la base mobile.
2. Déterminer
l'expression du vecteur accélération dans cette base mobile.
3. Que deviennent
ces expressions dans le cas d'un mouvement circulaire de centre O. La
vitesse angulaire q'
est notée w.

Mouvement de la station.
La station est considérée comme ponctuelle, assimilée à son centre
d'inertie G; sa masse est m.
Sa trajectoire est un cercle de centre O, centre de la terre.
1. Par analyse
dimensionnelle, donner l'unité de la constante de gravitation
universelle..
F = G
M m / d2 ; G = F d2 / (Mm).
Une force est une masse fois une accélération; elle s'exprime en kg m s-2.
G s'exprime en kg m s-2
m2 kg-2 soit : s-2 m3
kg-1 ..
2. Réaliser un
schéma représentant la force d'interaction gravitationnelle exercée par
la terre sur la station.
On note r = R +h.
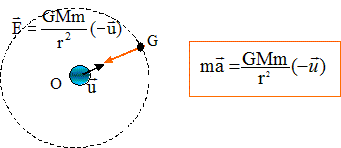
3. Dans le
référentiel géocentrique considéré comme galiléen, établir l'expression
de l'accélération de la station.
La
seconde loi de Newton conduit à :
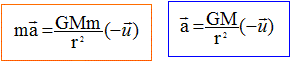
4. Quelle
est la qualification de ce type d'accélération ?
L'accélération est centripète.
5. Montrer que le
mouvement est uniforme.
La force de gravitation est constamment perpendiculaire à la vitesse.
Cette force ne travaille pas et ne modifie pas l'énergie cinétique de
la station. La norme du vecteur vitesse est constante : le mouvement
est uniforme.
6. Montrer que la
vitesse angulaire de la station est constante.
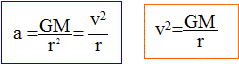 M masse de la terre. M masse de la terre.
De plus w = v / r = [GM / r3]½
= constante.
7. Déterminer l'expression de la
période T de la station.
La station décrit le
circonférence 2pr
en T seconde à la vitesse v.
T = 2pr
/ v = 2pr1,5 / (GM)½.
8. Déterminer l'expression de la
vitesse linéaire v en fonction de G, M, R et h.
v = [(GM / (R+h) ]½.
9.)Application numérique : R = 6,38
106 m ; M = 5,98 1024 kg ; h = 4,14 105
m ; G = 6,67 10-11 SI.
v = [6,67 10-11
x5,98 1024 / (6,38
106 + 4,14 105
)]½~7,66 103 m /s = 7,66 km /s.
T = 2 x3,14 x(6,38
106 + 4,14 105
) / (7,66 103) ~5573 s ou 93 min.
Les astraunotes obsrvent donc 16 levers de soleil chasue jour.
|
|
|
Etude énergétique.
1. Quelles sont les
unités des énergies potentielle, cinétique et mécanique ?
Le joule.
2. Déterminer l'expression de
l'énergie potentielle en fonction de G, M, r et m.
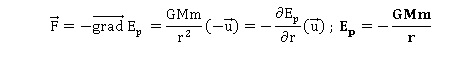
L'énergie potentielle de pesanteur étant nulle à l'infini, la constante
d'intégration est nulle.
3. Déterminer
l'expression de l'énergie cinétique en fonction de G, M, r et m.
Ec = ½mv2 avec v2 = GM / r ; Ec
=GMm / (2r) = -½Ep.
4. En déduire
l'expression de l'énergie mécanique.
E =Ep+Ec = -GMm / (2r) = ½Ep.
5. Application numérique.
m = 4,0 105 kg.
Ep = - 6,67 10-11 x 5,98 1024 x4,0 105
/(6,38 106 +
4,14 105 ) ~ -2,35 1013 J.
Ec = 1,17 1013 J.
E = -1,17 1013
J.
Détermination
du diamètre d'un fil d'araignée.
Première partie.
On note d le diamètre de ce fil.
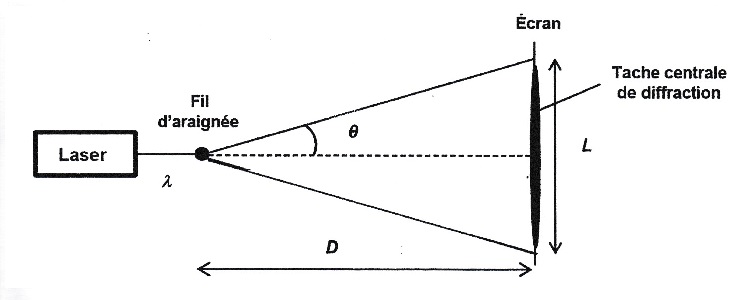
Ce fil est maintenu verticalement et éclairé par une source laser rouge
de longueur d'onde 615 nm. Le fil est proche de la source laser et
situé à une distance D d'un écran. On observe une figure de diffraction
sur l'écran caractérisée par une tache centrale de largeur L et un
angle de diffraction q.
1. Quel caractère
de la lumière est mis en évidence ?
La diffraction met en évidence le caractère ondulatoire de la lumière.
2. Rappeler
l'expression qui relie d, q,
l.
q = l /d.
3. Montrer que L =
2 lD / d.
L'angle q étant
petit tan q ~q = ½L / D=
l /d.
4. Application
numérique. D = 2 m ; L = 18,8 cm.
d = 2 l
D / L = 2 x 615 10-9 x 2 / 0,188
~1,31 10-5 m ~13 µm.
Partie 2. Etude de la
tenue mécanique du fil.
On considère que le rayon du fil est r = 2,5 µm.
Lorsque ce fil est étiré par une force F de faible valeur, il peut être
considéré comme un ressort et on a la relation DL = FL0 / (ES).
DL =
L-L0, allongement du fil ; E =8 109 SI module
d'Young du fil ; S section transversale du fil.
1. Par analyse
dimensionnelle, déterminer l'unité de E.
E = FL0 / (S DL).
Une force est une masse fois une accélération : kg m s-2.
L0 / DL
est sans unité et S est en m2.
Par suite E s'exprime en :
kg m-1 s-2.
2. Application numérique.
F = 0,03 N ; L = 7,7 cm ; L0 = 6,5 cm.
S = 3,14 x(2,5 10-6)2 = 1,96 10-11 m2.
E = 0,03 x 6,5 /(1,2 x1,96 10-11) ~8,2 109
kg m-1 s-2., en accord avec la valeur proposée.
3. Sachant que ce
fil peut s'allonger au maximum de 35 % avant de se casser, calculer la
masse maximale que l'on peut suspendre à ce fil.
On prendra g ~ 10 m s-2.
DLmaxi
= 6,5 x 0,35 =2,275 cm.
Fmaxi =DLmaxi
ES / L0 =
2,275 x8 109 x1,96 10-11 / 6,5~0,055 N.
Mmaxi =0,055 / 10~0,0055 kg ~5,5 g.
|
|
|
|
Pont de Wheastone.
Questions préliminaires.
1. Quelle est la
relation liant la tension aux bornes de la résistance R et l'intensité
la traversant.
U = RI.
2. Quel est le nom
de cette relation ?
Loi d'Ohm.
3. S'agit-il d'une
loi théorique ou expérimentale ?
En 1826, il s'agit d'une loi tirée de l'expérience.
Etude du pont.
R1 inconnue, R3 = 100 ohms, R4 = 5
kiloohms, R2 variable. E = 6 V.
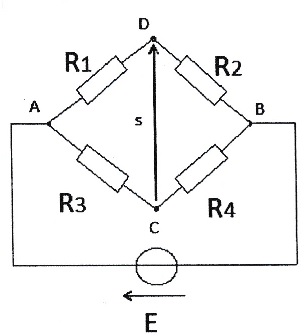 Si s = 0,001 V ; R1 =6,35 ohms. Si s = 0,001 V ; R1 =6,35 ohms.
1. Montrer que
l'expression de la tension s est : s = E(R2R3-R1R4)
/ [(R1+R2)(R3+R4)].
On note i1 l'intensité traversant R1 et R2
et i2 l'intensité traversant R3 et R4.
UAD = R1i1 ; UAC = R3i2
; UDB = R2i1 ; UCB = R4i2
;
s=UDC =UDA +UAC = UDB +UBC
= -R1i1 +R3i2 =R2i1
-R4i2 ;
(R1+R2)i1 =(R3+R4)i2
= E.
i1 =E / (R1+R2) ; i2 =E / (R3+R4)
;
s = -R1E / (R1+R2) +R3E
/ (R3+R4) ;
Réduire au même dénominateur.
2. A quelle
condition le pont est-il équilibré ?
s = 0 soit R2R3=R1R4.
3. Donner
l'expression de R1.
R1=R2R3 / R4.
4. Application
numérique. R2 = 1827 ohms lorsque le pont est équilibré.
R1= 1827 x100 / 5000 = 36,54 ~36,6 ohms.
5. A partir de
l'expression de s, déterminer l'expression de R1 en fonction
de s, R2, R3 et R4.
s = E(R2R3-R1R4) / [(R1+R2)(R3+R4)].
s (R1+R2)(R3+R4) = E
(R2R3-R1R4) ;
sR1(R3+R4) +ER1R4
= E R2R3-s R2(R3+R4)
;
R1 = [ E R2R3-s R2(R3+R4)
] / [s(R3+R4) +ER4].
6. Lorsque le
voltmètre qui mesure s indique zéro, cela signifie que cette tension
est comprise entre -1 mV et + 1 mV. En déduire la précision sur la
valeur de R1.
R1 = [ 6 x 1827 x100-s x1827x5100 ] / [5100s
+30000].
R1 = [1 096 200-7 787 700 s ] / [5100s +30000].
Si s = -0,001 V ; R1 =36,806 ohms.
Si s = +0,001 V ; R1 =36,274 ohms.
Différence : 0,532 ohms ; R1 = 36,54 ±0,27 ohms.
|
R1=
|
Radar de
recul.
Ce radar est basé sur des capteur ultrasonores qui se déclenchent
autamatiquement en marche arrière. L'afficheur indique la distance de
l'obstacle détecté pour des valeurs comprises entre 0,30 m et 2 m.
L'afficheur est équipé d'une alarme sonore dont la fréquence évolue en
fonction de la distance de l'obstacle.
Le radar est équipé de 4 capteurs identiques. Chaque capteur a une portée minimale dm = 0,30 m.
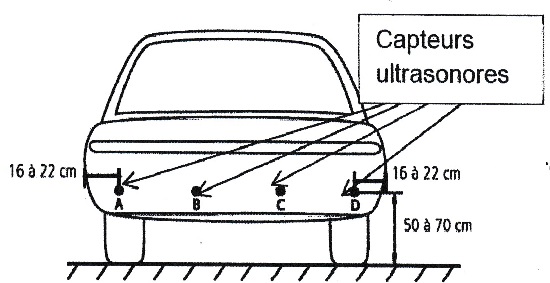
Le capteur est constitué d'un matériau piézo-électrique, capable de
fonctionner en mode émetteur et en mode récepteur.Il est efficace en
mode récepteur quand il a cessé d'émettre. Le capteur génère des salves
ultrasonnores de durée Dt1 = 1,7 ms avec une périodicité Dt2 = 12 ms. La fréquence de l'onde est d'environ 40 kHz.
L'onde émise par le capteur rencontre un obstacle, elle se
réfléchit et revient sur le capteur. Le capteur enregistre la durée Dt de cet aller-retour.
Questions.
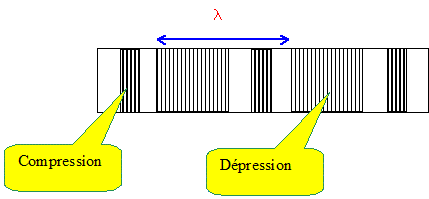
1. Quel est le type des ondes sonores ?.
Ondes longitudinales, propagation d'une variation de
pression.
2. Est ce que la célérité du son dépend deu milieu de propagation ?
Oui, 340 m/s dans l'air, 1500 m/s dans l'eau , 5000 m/s dans l'acier.
3. Définir milieu dispersif.
Dans un milieu dispersif, la célérité de l'onde dépend de sa fréquence.
4. Est-ce que l'air est un milieu dispersif pour les ondes sonores ? Non.
5. A partir de quelle fréquence, une onde sonore appartient-elle au domaine des ultrasons ?
Fréquence supérieure à 20 kHz.
Le capteur.
1. Pourquoi le terme de radar pour ce type de capteur est-il impropre ?
Un radar est un émetteur-récepteur d'ondes électromagnétiques qui
permet par retour de situer la position d'un objet, sa vitesse, lorsque
ce dernier fait obstacle et réfléchit les ondes.
Les ondes ultra-sonores ne sont pas des ondes électromagnétiques.
2. Calculer la valeur de la longueur d'onde des ultrasons.
l = c / f = 340 / 40 000 =0,0085 m = 8,5 mm.
3. Recopier l'enregistrement du signal du capteur et indiquer sur celui-ci les durées Dt1 et Dt2.
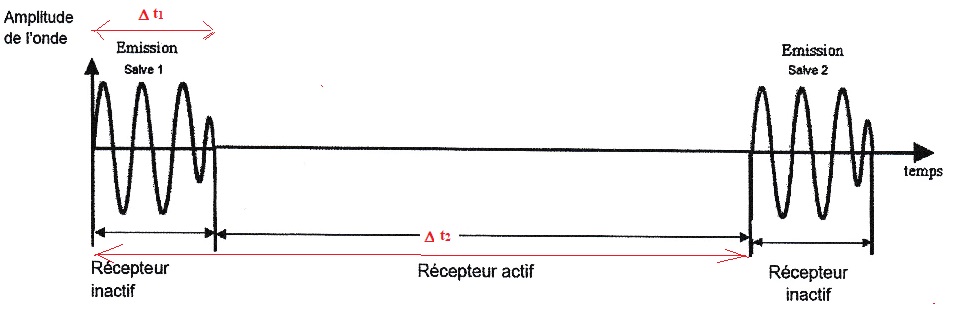
4. Montrer que la distance minimale de détection est d'environ 0,30 m.
Le récepteur est inactif durant 1,7 ms.
distance aller + retour = 340 x1,7 10-3 0,578 m puis diviser par 2. soit 0,29 m.
5.
Quelle caractéristique du signal de l'émission doit-on modifier pour
que le capteur puisse détecter un obstacle situé à une distance
inférieure à 0,30 m. Justifier.
Le capteur détecte un obstacle lorsqu'il fonctionne en récepteur. Il faut donc diminuer la durée de la salve ultrasonore.
6. Montrer que la valeur de la portée maximale est d'environ 2 m.
Distance aller-retour =12 x10-3 x340 = 4,08 m. Puis diviser par 2.
|
|