Les
champs magnétiques, Concours commun polytechnique 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Création
d’un champ magnétique« tournant »
On fait l’hypothèse d’être dans le cadre de l’ARQS :
on calcule le champ magnétique créé par des courants variables i(t),
comme en magnétostatique. En particulier, on peut utiliser le théorème
d’Ampère.
Q31. Énoncer les
équations de Maxwell dans le vide. Que deviennent-elles en régime
quasistationnaire ?
Les équations de Maxwell que doivent
vérifier respectivement le vecteur champ
électrique E et
le vecteur champ magnétique
B en notant r
la densité volumique de charge et
j le vecteur
densité de courant.
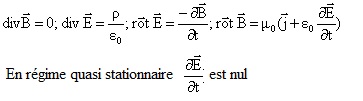
(e0 et
µ0 étant respectivement la
permittivité et la perméabilité du vide
: µ0 e0
c2 = 1).
Q32. Énoncer le
théorème d’Ampère.
On considère un ensemble de fils parcourus par des
courants, la circulation C du champ magnétique le
long d'une courbe fermée (G)
quelconque est :
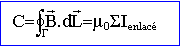 Q33. Après avoir
précisé les symétries du champ magnétique créé par un solénoïde unique
infini d’axe Δ, qui contient n spires par unité de longueur parcourues
par une intensité I, établir que celui-ci sépare l’espace en deux zones
de champ uniforme.
Q33. Après avoir
précisé les symétries du champ magnétique créé par un solénoïde unique
infini d’axe Δ, qui contient n spires par unité de longueur parcourues
par une intensité I, établir que celui-ci sépare l’espace en deux zones
de champ uniforme.
Tout plan perpendiculaire à l'axe de la bobine est
un plan de symétrie pour le courant : en
conséquence, le champ magnétique est
perpendiculaire à ce plan.
La distibution de courant étant invariante par
rotation autour de l'axe de la bobine, et par translation
sur cet axe, le champ est porté par l'axe de la
bobine et ne dépend que de la distance à
l'axe.
Le champ est nul à l'extérieur de la
bobine, car les lignes de champ ne sortent pas du
solénoïde.
Q34. On admet que
le champ extérieur est nul : établir l’expression du champ intérieur
créé par le solénoïde unique en fonction de μ0, n, I.
Appliquons le
théorème
d'Ampère au contour ABCD
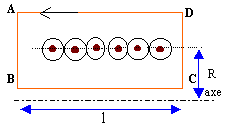
Le champ étant perpendiculaire à AB et
à CD, la circulation est nulle le long de AB et
CD.
Le champ est nul à l'extérieur, la
circulation du champ est nulle le long de AD.
La circulation du champ est µ0N
I le long de BC
µ0N I = B l.
B= µ0n
I avec n= N/ l , nombre de spire par
mètre.
Le champ est uniforme et colinéaire à l'axe
à l'intérieur du solénoïde.
On considère un ensemble de deux solénoïdes infinis identiques d’axes
Ox et Oy perpendiculaires concourants en O comme l’indique la figure
suivante. Les spires sont considérées comme circulaires car réalisées
sur un cylindre de rayon R comportant n spires jointives par unité de
longueur. Les spires du solénoïde d’axe Oy sont parcourues par une
intensité Iy = I0 cos(Ωt + α) et celles du
solénoïde d’axe Ox par une intensité Ix = I0cos(Ωt).
L’orientation des courants correspond au sens direct autour des axes
respectifs.
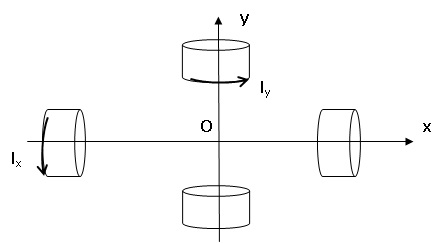
Q35. Établir que le champ magnétique dans la zone commune aux deux
circuits, pour un déphasage α = π/2, est un champ « tournant » , c’est-à-dire
un champ de norme constante B1 porté par une direction de vecteur unitaire u qui tourne à vitesse
uniforme dans le plan xOy. On précisera sa norme B1 et sa vitesse de rotation W.
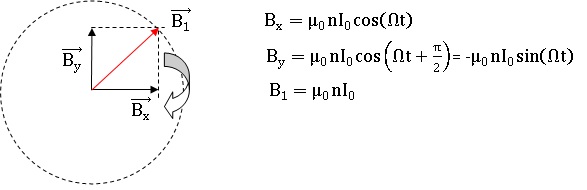
Il est en réalité difficile de produire des champs tournants autour des
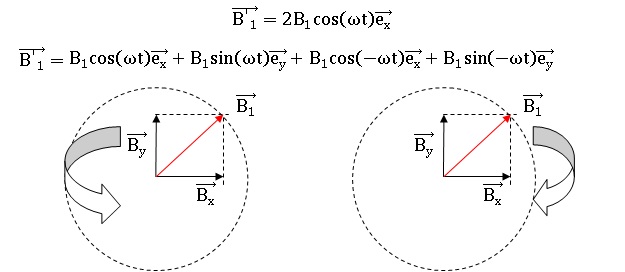
patients. On utilise donc un champ oscillant créé par une bobine unique d’axe Ox : B′1 = 2B1
cos(ωt) .
Q36. Montrer que ce champ est équivalent à la superposition de 2 champs
de même amplitude (à préciser) qui tournent en sens opposé à la même vitesse.
|
|
|
II.2- Création d’un champ permanent intense B0.
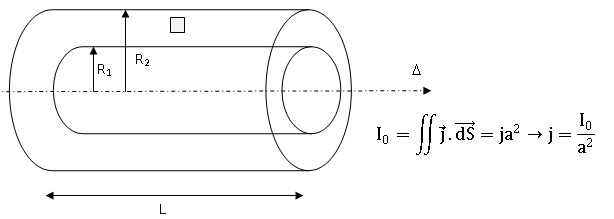
On utilise un solénoïde « épais » (épaisseur e = R2 − R1) considéré comme la superposition de solénoïdes infinis (en réalité de longueur L >> R2)
de même axe Oz. Il est réalisé par un empilement jointif de spires de
section carrée, de côté a = 1,0 mm, enroulées sur un cylindre de
longueur L = 4,0 m, depuis un rayon R1 = 20 cm jusqu’à un rayon R2 = 25 cm. Les spires sont des fils de cuivre parcourus par un courant continu I0 uniformément réparti, orienté dans le sens direct autour de Oz. Les sections carrées sont en
positionnement radial.
Q37. Calculer le vecteur densité volumique de courant pour R2 > r > R1.
Q38. Établir que l’expression du champ sur l’axe vaut B = μ0I0 / a2 (R2 − R1).
B = µ0n I0 avec n = Ntotal / L et Ntotal = L(R2-R1) / a2. B = μ0I0 / a2 (R2 − R1).
Q39. Quelle est l’intensité nécessaire pour engendrer un champ de 1 Tesla ?
I0 = B a2 / (µ0(R2 − R1))= 1 x10-6 / (4 x3,14 10-7 x(0,25-0,20))~16 A.
Pour obtenir un champ intense, sans problème d’échauffement, on utilise
des matériaux supraconducteurs qui perdent totalement leur résistivité
en dessous d’une température critique TC, qui dépend du
champ magnétique. Ces matériaux ont des propriétés magnétiques
intéressantes : en régime permanent, ils « expulsent » le champ
magnétique. Dans le cadre médical, on utilise des
supraconducteurs durs, pour lesquels TC < 133 K pour B > 0,2 T.
La loi constitutive de certains supraconducteurs est 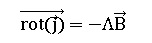 avec Λ > 0. avec Λ > 0.
Q40. Quelle est l’unité de cette constante Λ ?
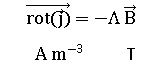 Λ s'exprime en A T-1 m-3. Λ s'exprime en A T-1 m-3.
Q41. En supposant qu’on peut appliquer les équations de Maxwell du vide dans le matériau supraconducteur de perméabilité μ0 et de permittivité є0, exprimer l’équation différentielle à laquelle obéit le champ magnétique en régime permanent.
Q42. Faire apparaître dans l’équation différentielle obtenue une grandeur homogène à une longueur notée δ.
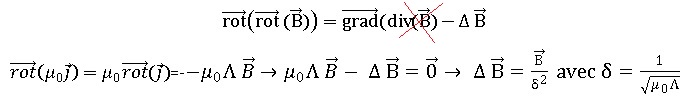
On considère qu’un supraconducteur de ce type occupe un demi-espace x
< 0 et que les sources du champ sont telles que règne dans l’espace
extérieur un champ permanent uniforme 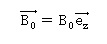 . La modélisation des distributions est volumique et n’introduit donc pas de discontinuités spatiales du champ magnétique. . La modélisation des distributions est volumique et n’introduit donc pas de discontinuités spatiales du champ magnétique.
Q43. En utilisant les invariances du problème, montrer que le champ dans le supraconducteur s’écrit sous la forme
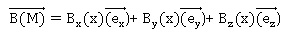
La situation est invariante par translation le long de y ; il en est de
même le long de z. par contre il n'y a pas d'invariance le long de x,
le supraconducteur occupant le demi-espace x <0.
Q44. Expliciter le champ permanent régnant dans le supraconducteur.
Dans l'espace extérieur au supraconducteur, le champ est dirigé suivant
z ; donc dans le supraconducteur le champ est dirigé suivant cet axe z
et il dépend de la variable x.
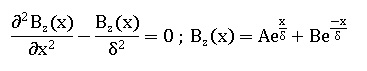
Conditions aux limites : quand x tend vers moins l'infini, le champ est nul, donc B = 0.
Quand x = 0, le champ est égal à B0, donc A = B0.
B = B0 exp (x / d) avec x négatif ou B = B0 exp (-x / d) avec x positif.
Q45. En déduire la densité de courant volumique.
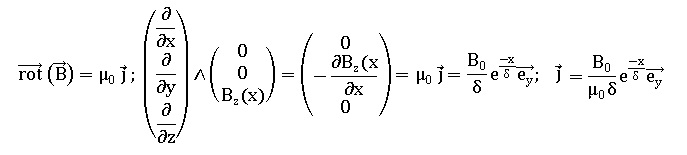
Q46. L’ordre de grandeur du paramètre δ est de 5.10–8 m. Commenter.
d << R2-R1. Le champ pénètre uniquement la surface du supraconducteur.
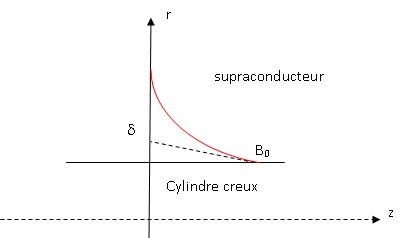
Q47. Tracer, sans faire de calculs, l’allure de Bz(r)
dans une symétrie cylindrique où le supraconducteur occupe le volume
d’un cylindre creux d’épaisseur 100 δ, de longueur L très grande devant
son rayon R, lui-même très supérieur à 100 δ. On suppose que le champ
vaut B0 dans l’espace intérieur au cylindre creux.
|
|