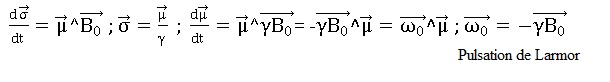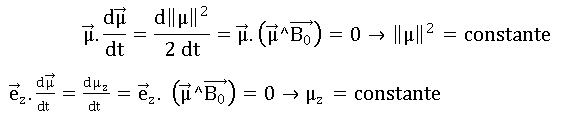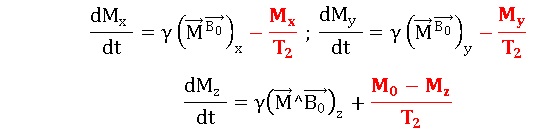Comportement
d'une population de dipôles dans un champ magnétique,
concours Concours commun polytechnique 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Partie I
– Comportement d’une population de dipôles dans un champ magnétique.
I.1- Dipôles magnétiques
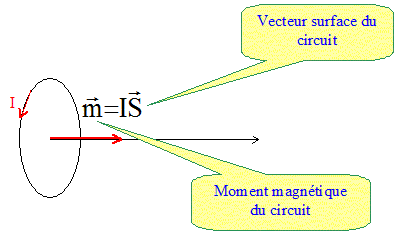
Q1. Définir le vecteur moment magnétique associé à une
boucle circulaire de courant de rayon R et
d’axe de révolution Oz, parcourue par une intensité I, dans le cadre de
l’approximation dipolaire .Le sens de rotation directe autour de l’axe
Oz est le sens d’orientation de l’intensité algébrique.
Q2. Expliquer pourquoi une sphère
chargée, en rotation autour d’un axe passant par son centre, est
elle-aussi caractérisée par un moment magnétique dont on précisera la
direction et le sens (on ne
demande pas le calcul du moment mais seulement la justification de son
existence).
Une charge en mouvement crée un courant.
Une charge en rotation autour d'un axe crée une boucle circulaire de
courant. La sphère chargée en rotation autour d'un axe passant par son
centre, peut être considérée comme un empilement de boucles de courant.
Une telle sphère possède donc un moment magnétique dirigé suivant l'axe
de rotation de la sphère.
Dans le cas du proton (noyau d’hydrogène)
qui tourne sur lui-même (rotation propre de vecteur de
rotation W autour
d’un axe Oz), on peut lui associer un moment magnétique µP
colinéaire à W.
Q3. Justifier par
analyse dimensionnelle l’unité (J T-1) écrite dans le
tableau de données.
Le moment d'une force s'exprime en N m et le champ magnétique en tesla
( T). Le moment magnétique s'exprime en N m T-1.
Le newton mètre (N m) est homogène à une énergie ( J).
Soit un dipôle magnétique de moment µ placé en O dans un champ
magnétique extérieur uniforme
permanent B0.
Q4. En déduire
quelles sont les 2 positions d’équilibre d’un moment dipolaire
magnétique, dans un
champ magnétique extérieur uniforme B0, en précisant les
valeurs associées de l’énergie
potentielle.
Energie potentielle d'interaction entre ce dipole et le champ
magnétique extérieur.
Ep = - µ B0 cos q, q étant l'angle formé entre
le moment magnétique et le champ magnétique B0.
Ep est minimale -µB0 ( équilibre stable) lorsque
le champ magnétique B0 et le dipole sont alignés.
Ep est maximale +µB0
( équilbre instable) lorsque le champ magnétique B0 et le
dipole sont antiparallèles.
Q5. Évaluer la différence d’énergie
en eV entre les deux configurations d’équilibre d’un noyau
d’hydrogène soumis à un champ magnétique permanent de 1 tesla (ordre de
grandeur typique en
RMN).
DEp
= 2 µPB0 =2 x1,4 10-26 x1 = 2,8 10-26
J.
ou 2,8 10-26 / (1,6 10-19) = 1,75 10-7
eV.
Q6. Comparer cette valeur
à celle de l’énergie thermique à 37 °C.
Ethermique = k T = 1,4 10-23 x(273+37)=4,34 10-21
J
Ethermique >>DEp . L'énergie
thermique est suffisante pour faire passer le proton d'un état
d'équilibre à un autre.
Q7. L’ordre de
grandeur de l’énergie de liaison covalente de OH dans l’eau est de 5 eV
et celui d’une
énergie d’ionisation est de 13,6 eV. Justifier l’utilisation de la RMN
en imagerie médicale, en
considérant que la méthode fait passer le proton d’un état d’équilibre
à l’autre.
DEp est très
inférieure à l'énergie de liaison covalente OH ainsi qu'à l'énergie
d'ionisation des molécules. L'énergie apportée par le champ magnétique
extérieur ne peut ni endommager les liaisons chimiques ni ioniser les
moléculzq du corps humain.
Nous
considérons qu’une population de dipôles, placés dans un champ
magnétique extérieur B0 de
1 tesla, en équilibre thermique à la température T, obéit à la
statistique de Boltzmann.
Q8. Rappeler, à un
facteur multiplicatif près, l’expression de la probabilité d’occuper un
état d’énergie
E par un dipôle.
p(E) = 1 / Z exp(-E / (kT)).
Q9. Évaluer le rapport des populations NN+
/ NN-
, en équilibre thermique à la température T, NN+
étant la
densité volumique de dipôles de plus grande énergie et NN-
étant la densité volumique de dipôles
de plus petite énergie (on admettra que l’on peut effectuer un
développement limité à l’ordre 1).
NN+ / NN- = exp(-µPB0 /
(kT)) / exp(+µPB0
/ (kT)) =exp(-2µPB0
/ (kT)).
Or µPB0 / (kT)
<< 1, d'où : NN+
/ NN- ~1-2µPB0
/ (kT)
Q10. À quelle orientation correspond
la population la plus nombreuse à l’équilibre thermique ?
A
l'équilibre thermique NN+ < NN-
.
On note h = (NN- -NN+)
/
(NN- +NN+) la différence relative de population entre
les deux niveaux.
Q11. Exprimer, à
l’équilibre thermique, la différence relative h = h0 (toujours à l’ordre 1) en
fonction de µ, k, T et B0.
1-NN+ / NN- =2µPB0
/ (kT) ; (NN-
-NN+
) / NN- =2µPB0 / (kT) ; (NN- -NN+
) = 2NN- µPB0 / (kT).
1+NN+
/ NN- =2-2µPB0
/ (kT) ; (NN-
+NN+
) / NN- =2+2µPB0 / (kT) ; (NN- +NN+
) = 2NN- (1+µPB0 /
(kT)).
µPB0 /
(kT) << 1, h0=µPB0
/ (kT).
Q12. Donner sa valeur numérique
pour des protons placés dans un champ de 1 tesla, à une température
de 37 °C et commenter.
h0=1,4
10-26 / (1,4 10-23 x310) ~3 10-6
<<1.
La probabilité de trouver un proton dans l'état énergétique haut
est à peu près identique à celle de le trouver dans l'état
énergétique bas.
|
|
|
I.2-
Rapports gyromagnétiques
Une boucle de courant est créée par un électron dans son mouvement
orbital autour du noyau. On considère l’orbite circulaire, de rayon rB.
Q13. Exprimer le
moment magnétique µe associé à cette boucle de courant en
fonction du rayon rB, de la vitesse v et de constantes
fondamentales.
Q14. Exprimer le moment cinétique
de l’électron, par rapport au point O,en fonction des mêmes paramètres.

Q15. Exprimer le
rapport gyromagnétique correspondant en fonction des constantes fondamentales
et calculer la valeur numérique du rapport gyromagnétique de l’électron.
ge=µe
/ se =
-e / (2me) =1,6 10-19 /(2 x9,1 10-31)=8,79
1010 C kg-1.
Le corps humain est essentiellement constitué d’eau : l’hydrogène
représente 10 % de la masse corporelle, c’est-à-dire 86 % de la
composition chimique de notre organisme. On étudiera donc, par la
suite, le comportement de ces protons soumis à un champ magnétique
extérieur B0..
On peut, comme dans l’exemple de l’électron, associer au proton un
rapport gyromagnétique égal au rapport de son moment magnétique et de
son moment cinétique. Pour l’hydrogène H isolé, le rapport
gyromagnétique, qui vaut gp
= 2,67.108 rad.s–1.T–1, est associé à
un moment cinétique quantifié qui ne peut prendre que les valeurs ± h /2
Q16. Les valeurs
ci-dessus sont-elles conformes à la valeur du moment magnétique μp
?
µp = gp
sp
= 2,67 108 x1,05 10-34 / 2 = 1,4 10-26
J T-1. Donc conformité des valeurs.
Q17. Exprimer en
fonction de B0 et gp
la fréquence du photon qui permet le passage du niveau de plus basse
énergie au niveau de plus haute énergie pour l’hydrogène.
Q18. Quelles sont
la fréquence et la longueur d’onde λ correspondantes pour un champ
permanent de 1 tesla ?
DE = 2 µp B0
= h n ; n =2 x1,4 10-26
x1 / (6,63 10-34)=4,2 107 Hz = 42 MHz.
l = c
/ n =3 108
/ (4,2 107) =7,1 m.
I.3- Précession d’un dipôle.
On écarte un dipôle d’un angle α par rapport à la position d’équilibre
stable dans un champ magnétique B0.
Q19. Écrire
l’équation différentielle caractéristique de l’évolution du vecteur
moment dipolaire .
Ecrire le théorème du moment cinétique :
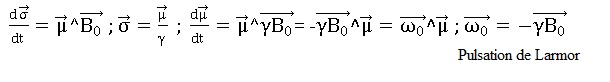
Q20. Montrer que sa
norme se conserve et que la projection du moment sur l’axe du champ
magnétique se conserve aussi.
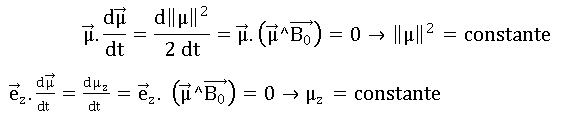
Q21. Décrire le
mouvement de la projection du vecteur dans un plan orthogonal au champ
magnétique.
La projection du mouvement du moment magnétique du dipôle dans un plan
perpendiculaire au champ B0 est un mouvement circulaire
uniforme de pulsation w0.
Q22. Décrire le
mouvement complet du dipôle en vous appuyant sur un dessin. Préciser le
sens du mouvement de précession.
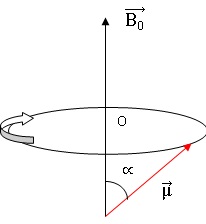
Lorsque les protons étudiés se trouvent dans une molécule (ou un
cristal), les liaisons chimiques entre atomes modifient la fréquence de
résonance précédente par modification du rapport gyromagnétique. Mais
ces effets sont très petits (ils sont généralement mesurés en parties
par million ou ppm). Il faut donc des instruments très sensibles pour
distinguer entre protons libres et protons engagés dans une liaison
chimique.
|
|
|
|
I.4- Précession de l’aimantation.
À l’état naturel, les vecteurs moments dipolaires des noyaux
d’hydrogène sont répartis dans toutes les directions et il n’y a pas
d’effet magnétique global pour un échantillon. Par contre, en présence
d’un champ magnétique extérieur, l’hydrogène aura des propriétés
magnétiques caractérisées par un vecteur moment magnétique global
volumique appelé aimantation M. En IRM, c’est ce vecteur aimantation M
, obtenu en présence d’un champ magnétique extérieur, qui permet
d’obtenir des images des tissus du corps humain.
On considère l’état d’équilibre thermique d’un échantillon contenant
des hydrogènes en présence d’un seul champ fort permanent B0.
On suppose, pour simplifier, que le système des dipôles magnétiques
associés aux protons peut être décrit comme un système à 2 états ne
pouvant occuper que les positions parallèles (vecteur moment dipolaire
et champ magnétique de même sens) ou antiparallèles (vecteur moment
dipolaire et champ magnétique de sens contraire), décrites à la
question Q4 .
Q23. Comment est
orienté le vecteur aimantation de norme M0 ?
Le vecteur aimantation et le vecteur champ magnétique sont parallèles
de même sens.
Q24. Exprimer la
valeur de M0 en fonction du nombre N de noyaux d’hydrogène
par unité de volume, de h
et de μp.
M0 = -µpN+ +µpN-
=µp(-N+ +N- )=h N µp.
En mécanique quantique, le moment cinétique du noyau d’hydrogène est
quantifié en projection sur l’axe Oz par σz = ± h / (2π) S =
± h S,
avec S =½.
Q25. Exprimer M0
à partir du nombre N de noyaux d’hydrogène par unité de volume, du
rapport gyromagnétique gp
du proton, du champ magnétique B0, de la température T et
des constantes de Planck et de Boltzmann.
M0 =h N
µp=h N gpsp=h N gp h / 2=µpB0
/ (kT) N gp h / 2=N ( gp h / 2)2 B0
/ (kT).
Q26. Évaluer la
concentration volumique des noyaux d’hydrogène (exprimée en m–3)
en assimilant le corps humain à de l’eau (masse molaire de l’eau H20
: m = 18 g.mol–1 et masse volumique de l’eau ρ = 1,0 g.cm–3).
Nombre de molécule d'eau par unité de
volume : r Na / m = 1000
x 6,02 1023 / 0,018 =3,34 1028 m-3 .
Chaque molécule d'eau compte deux protons ; nombre de protons par
unité de volume : 6,7 1028 m-3 .
Q27. Comparer le
champ créé par ce dipôle global à une distance de 1 m sur son axe au
champ permanent B0 = 1 T.
B = µ0M cos q
/ (2pr3)
avec q = 0 ou p.
M = h N µp=
3 10-6 x 6,7 1028 x1,4 10-26=2,8 10-3.
Norme de B = 4 p
10-7 x 2,8 10-3 / (2 p) = 5,6 10-10 T.
Q28. Justifier
l’introduction d’un champ perturbateur qui change la direction de
l’aimantation.
Le champ B0, très intense par rapport au champ créé par
l’aimantation, ne permet pas l’étude sur Oz.
On va donc étudier l’évolution dans le temps du vecteur aimantation M
qui caractérise l’ensemble des moments dipolaires des protons présents
dans l’échantillon. Si on provoque un changement de l’orientation des
moments magnétiques, l’aimantation va tendre à retourner à sa valeur à
l’équilibre thermique avec un temps de relaxation ou temps
caractéristique.
Q29. Interpréter
les équations de Bloch en précisant à quel couple supplémentaire C est
soumis le vecteur aimantation pour traduire le phénomène de relaxation.
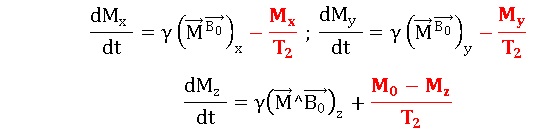
Les coordonnées du couple supplémentaire sont indiquées en rouge
ci-dessus.
Q30. Quel est le
domaine des radiofréquences ? Est-ce conforme au résultat de la
question Q18.
Fréquences comprises entre 3 Hz et 300 MHz.
Longueur d'onde comprises entre 1 m et 100 000 km.
|
|
|