QCM
physique, gravitation, numérisation, photons,
concours Avenir 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
Répondre à 45 questions
au choix parmi les 60 proposées. Sans cakculatrice.
Une
seule réponse exacte par question ; chaque réponse exacte rapporte + 3
points ; chaque réponse fausse enlève 1 point.
Exercice 1. Le décollage
et la station ISS.
Thomas Pesquet décolle le 17 novembre 2016 à 20 h 20
TUC à bord
d'un vaisseau Soyouz. Le Soyouz MS-03 est placé en orbite par une fusée
Soyouz tirée depuis le cosmodrome de Baïkonour au Kazakhstan. On
étudiera dans un premier temps la phase de décollage de la fusée,
ensuite son mouvement une fois les réacteurs éteints et enfin le
mouvement de la station spatiale sur son orbite autour de la
Terre. On donne g = 9,8
N kg-1.
On étudie le décollage de la fusée par rapport au référentiel
terrestre. Durant son décollage, grâce à ses moteurs qui éjectent des
gaz, la fusée acquiert une accélération qui lui permet de décoller.
On désignera par mf la masse de la fusée, mg la
masse des gaz éjectés, vf la vitesse de la fusée vg
la vitesse des gaz. Le système (fusée+gaz) sera considéré comme
pseudo-isolé.
1. Afin de pouvoir décoller et
quitter le sol terrestre, la fusée doit acquérir une accélération de
norme :
A) nulle
B) infériieure à g.
C) égale à g.
D) supérieure à g. Vrai.
La poussée des moteurs
doit être supérieure au poids de la fusée.
2. Au moment du
décollage, la quantité de mouvement du système (fusée+gaz), est :
Le système {fusée + gaz
éjecté} est pseudo-isolé et sa vitesse initiale est nulle.
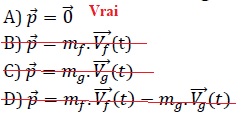 . .
3. Au
cours du décollage, la quantité de mouvement du système (fusée+gaz) :
A) diminue
B) reste constante.
Vrai.
Le
système { fusée + gaz } reste pseudo-isolé.
C) augmente.
D) est nulle.
Lorsque les réacteurs s’éteignent, la fusée se situe à une altitude h
du sol terrestre et a une vitesse de coordonnées (VOx, VOy)
dans le repère (Oxy). Durant cette phase, la fusée n’est soumise qu’à
son poids. Les frottements avec l’air seront négligés. La fusée sera
assimilée à un corps ponctuel noté f.

4. Les coordonnées de la
vitesse initiale dans le repère (Oxy) sont :
A) (V0 ; 0)
B) (0 ; V0).
C) ( V0 sin a ; V0 cos a) Vrai.
D)
( V0 cos a ; V0 cossin a).
5. Pour déterminer
l’accélération, on utilisera ici :
A) la 1ère loi de Newton
B) la 2ème loi de
Newton. Vrai.
C) la 2ème loi de Kepler
D) la 3ème loi de Kepler
6. L’accélération
de la fusée pendant cette phase a pour expression :

La fusée n'est soumise
qu'à son poids.
7.
Pour obtenir l’expression des coordonnées de la fusée en fonction du
temps, il faut :
A) dériver l’accélération
B) dériver la dérivée de l’accélération
C) obtenir la primitive de l’accélération
D) obtenir la
primitive de la primitive de l’accélération. Vrai.
8. Les coordonnées de la vitesse de
la fusée en fonction du temps sont :
A) Vx(t)
= V0 sin a
; Vy(t) = -gt + V0 cos a. Vrai.
B) Vx(t)
= V0 sin a
; Vy(t) = +gt + V0 cos a
C) Vx(t)
= V0 cos a
; Vy(t) = -gt + V0 sin a.
D)
Vx(t) = V0 cos a ; Vy(t) = -gt -
V0sin a.
9. Les coordonnées de la position de la fusée en
fonction du temps sont :
A) x(t) = V0 sin a t ; y(t) =
½gt2+ V0 cos a + h .
B) x(t) = V0 sin a t ; (t) =
-½gt2+ V0 cos a + h Vrai.
C) x(t)
= V0 cos a
t ; y(t) = -½gt2+ V0 sin a + h
D)
x(t) = V0 cos a t ; y(t) = +½gt2+
V0
sin a + h.
|
|
|
|
Soyouz
MS-03 est maintenant arrimée à la Station Spatiale Internationale ISS
dont nous allons étudier ici quelques paramètres. On supposera que la
Station Spatiale Internationale ne subit que l’attraction
gravitationnelle de la Terre.
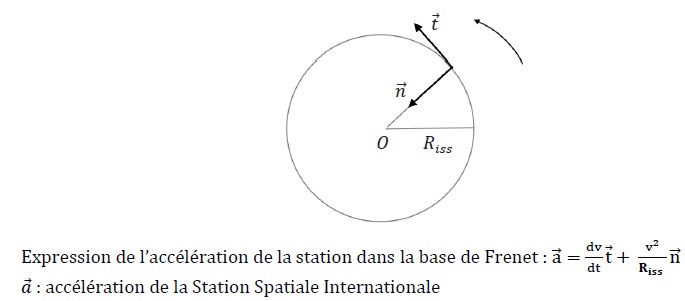
v : norme de la vitesse de la station.
Riss distance entre la station et le centre de la terre.
10)
Pour étudier la trajectoire de la Station Spatiale Internationale ISS
(masse MS) autour de la Terre (masse MT), il faut se placer dans le
référentiel :
A) héliocentrique
B) géocentrique. Vrai.
C) terrestre
D) de Kepler
11) Une des lois
de Kepler permet de relier la période d’un Astre sur son orbite au
rayon de celle-ci. Il s’agit :
A) de la 1ère loi de Kepler
B) de la 2ème loi de Kepler
C) de la loi des aires
D) de la 3ème loi
de Kepler. Vrai.
12. La période de révolution de la
Station Spatiale Internationale en fonction de rayon est :
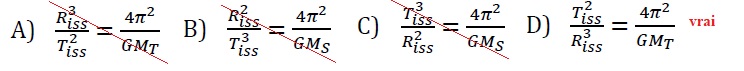
13) En doublant la
distance entre la Station Spatiale Internationale et la Terre, la
période de révolution de la station sera :
A) multipliée par 2
B) multipliée par
radical(8) ; (8 ½). Vrai.
Riss
3 est multiplié par 8 ; T2
est multiplié par 8 ; T est multiplié par 8½.
C) multipliée par 4
D) multipliée par 8
14)
L’expression de la force subie par la Station Spatiale Internationale
est :
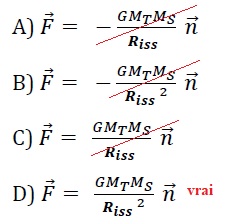
15) L’accélération
de la station est :
A) centripète. Vrai.
B) centrifuge
C) tangente à la trajectoire
D) nulle
.
16)
En utilisant la 2ème loi de Newton et l’expression de l’accélération de
la station dans la base de Frenet, on obtient l’expression suivante de
la norme de la vitesse de la Station autour de la Terre :
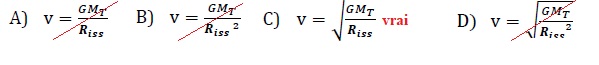
17) La période de
révolution de la Station sur son orbite est :
La station décrit la
circonférence 2pRiss à le vitesse v en Tiss
seconde.
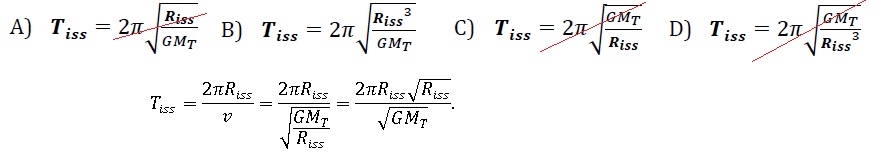
18) L’énergie
mécanique de la Station Spatiale Internationale au cours du temps :
A) diminue
B) augmente
C) reste constante.
Vrai.
D) est nulle.
Exercice 2 : Communication
avec la Terre.
Afin de communiquer avec la Terre, Thomas Pesquet utilise des outils à
sa disposition pour transmettre et garder des informations.
Toutes les données de la mission seront stockées sur des disques
optiques d’indice de réfraction n. La surface de stockage d’un disque
est comprise entre un cercle de rayon Rint=2 cm et un cercle
de rayon Rext = 7 cm. La piste, gravée sur la surface de
stockage, est une spirale dont le pas est de 0,5 µm.
Lors de la lecture du disque, une diode laser de longueur d’onde dans
le vide égale à 600 nm parcourt la piste. La vitesse moyenne de lecture
de la piste est de 4 km /s.
Données : On note c la célérité des ondes électromagnétiques dans le
vide
Indice du disque optique de stockage n = 1,5.
Constante de Planck : h ~6 10-34 SI.
Vitesse v d’une onde électromagnétique dans un milieu d’indice n : v =
c / n.
1 eV = 1,6.10-19 J
19) Pour qu’un
signal analogique de période T soit correctement numérisé, il doit être
échantillonné avec une période d’échantillonnage telle que :
A) Te
<< ½T. Vrai.
B) Te
<< T.
C) Te
>> T.
D) Te
>> ½T.
La fréquence
d'échantillonnage fe doit être supérieure à 2 f.
1 / Te
>> 2 / T soit Te << ½T.
20)
La qualité de la numérisation dépend de la quantification qui est liée
au nombre de bits utilisés. Avec 4 bits, la résolution est :
A) R = 4
B) R = 8
C) R = 16. Vrai ( 24
= 16)
D) R = 32.
21) Une image a une
définition en pixels de 2000 x 4000 et un codage en RVB. La taille
d’une image est de :
A) 8 Mo
B) 24 Mo. Vrai.
C) 64 Mo
D)4,1 Go.
2000 x 4000 x3 = 2,4 107
octets = 24 Mo.
|
|
|
|
|
22) Si le débit de la connexion
entre la station est la Terre est de 10 Mbit / s, la durée de
transmission d’une image est de :
A) 2,4 s.
B) 6,4 s.
C) 12,6 s
D) 19,2 s. Vrai.
Taille d'une image : 2,4 107
octets =2,4 107 x8 = 1,92 108 bits = 192 Mbits.
192 / 10 = 19,2 s.
23)
La fréquence de la radiation utilisée pour la lecture des informations
sur le disque est :
A) f = 1. 1014 Hz.
B) f = 3. 1014
Hz.
C)
f = 5. 1014
Hz. Vrai.
D)
f = 6. 1014 Hz.
f = c / l = 3 108 /(600
10-9) = 5. 1014
Hz.
24.
La célérité de la radiation dans le disque optique est :
A) v = 1,0 108 m /s
B) v = 1,5 108
m /s
C)
v = 2,0 108
m/s. Vrai.
D) v
= 3,0 108 m /s
v = c / n = 3,0 108
/ 1,5 = v = 2,0 108 m /s
25)
La longueur d’onde de la radiation lors de sa propagation dans le
disque optique est :
A) 400 nm. Vrai.
B) 500 nm
C) 600 nm
D) 700 nm.
l = v / f = 2,0 108
/ ( 5 1014) = 2 / 5 10-6
= 0,4 10-6 m = 400 nm.
26)
La lecture du disque optique repose sur le phénomène :
A) d’absorption
B) d’émission
C) de diffraction
D) d’interférences.
Vrai.
27)
La surface de stockage de l’information sur le disque optique est
d’environ :
A) S ~ 1,1 10-3 m2.
B) S
~ 1,4 10-2 m2. Vrai.
C) S
~ 1,7 10-2 m2.
D) S
~ 2,0 10-2 m2.
S = p ( Rext2
-Rint2)
~3x (72 -42) 10-4 = 1,35 10-2 m2.
28)
La longueur de la piste de lecture sur le disque est d’environ :
A) 7 km
B) 10 km
C) 28 km. Vrai.
D) 40 km.
Surface / pas = 1,4 10-2
/ ( 5 10-7) = 1,4 / 5 105
= 0,28 105 m = 28 km.
29) Les
informations sur le disque optique sont lues par le lecteur en à peu
près :
A) 1 s
B) 2,5 s
C) 7 s. Vrai.
D) 20 s.
Longueur de la piste /
vitesse de lecture = 28 / 4 = 7 s.
|
|
30)
Dans le vide, la valeur de la quantité de mouvement ( kg m s-1)
des photons utilisés est :
A) 3,6 10-41.
B) 1,0 10-36.
C) 3,6 10-32.
D) 1,0 10-27.
Vrai.
p = h / l = 6 10-34 /
(600 10-9) = 1,0 10-27 kg m s-1.
31) La constante de
Planck a pour unité dans le système international :
A) kg s s-2.
B) kg s-1.
C) kg m2 s-1. Vrai.
D) kg m s-1.
h = énergie (J) /
fréquence ( s-1) ; h s'exprime en J s.
Une énergie est une force
fois un déplacement et une force est une accélération fois une masse.
L'énergie s'exprime en kg
m s-2 m =kg m2 s-2 .
32) La lumière
émise par le laser transporte une énergie de l’ordre de :
A) 1,0 10-36 J
B) 1,236 10-32 J
C) 3 10-19 J.Vrai.
D) 36 10-19 J
E = h c / l
~ 6 10-34
x 3 108 /(600 10-9)
~ 3 10-19 J.
33) Une diode laser
est composée en partie d’un semi-conducteur contenant des électrons qui
peuvent s’exciter ou se désexciter. Les photons émis par la diode
laser proviennent du passage des électrons d’une bande de conduction
vers une bande de valence. L’énergie EG séparant ces deux
bandes est de :
A) 1 eV
B) 2 eV. Vrai.
C) 3 eV
D) 4 eV
E = 3 10-19
J = 3 10-19 / ( 1,6 10-19)
~ 2 eV.
34) Dans
l’univers, certaines particules se déplacent en mouvement rectiligne
uniforme par rapport au référentiel terrestre considéré comme galiléen
avec une vitesse v proche de celle de la lumière. On peut, dans ces
conditions, observer que le temps s’écoule :
A) plus lentement
dans le référentiel propre des particules que dans le référentiel
terrestre. Vrai.
B) plus lentement dans le référentiel terrestre que dans le référentiel
propre des particules
C) de la même manière dans le référentiel propre des particules et dans
le référentiel terrestre
D) de la même manière dans tout référentiel.
35) La formule de
Lorentz (Dt1
= g Dt2
) relie les durées mesurées entre deux évènements dans les deux
référentiels, terrestre et propre. Pour un facteur de Lorentz g=2, la vitesse v du système
par rapport au référentiel terrestre est :
A) c ;
B) 0,75 c.
C) (3 / 4)½c.
Vrai.
D) 0,5 c.
g = 1 /(1-(v/c)2)½ = 2 ; 1 /(1-(v/c)2)
= 4 ; 1-(v/c)2) = 0,25 ; (v/c)2) = 3 / 4. |
|
|