Equation
différentielle, étude de fonctions, BTS groupe D 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
2 .
Le refroidissement rapide des barquettes
de plats cuisinés doit être opéré de telle manière que leur température
ne demeure pas entre 10°C et 63°C pendant plus de 2 heures.
Partie A.
On procède à deux réglages différents de
la cellule de refroidissement
rapide ( réglage n°1 et réglage n°2 ). Sur le graphe ci-dessous sont
représentées les courbes C1 et C2 qui
correspondent respectivement à la
température d'une barquette placée dans la cellule en fonction du temps
pour le réglage n°1 et n°2.
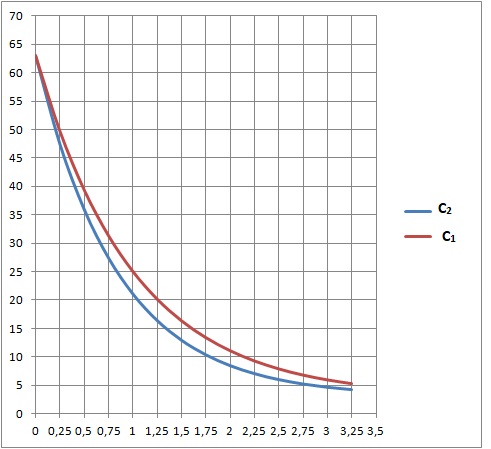
1. Indiquer la température de la barquette au bout de 90 minutes dans la cellule de refroidissement rapide avec le réglage n°1.
90 minutes = 1,5 heures. Le graphe indique 19°C ( courbe C1).
2.a. Le réglage n°1 satisfait-il à la réglementation ? Justifier.
Au bout de 2 heures, la température lue sur la courbe C1 est voisine de 12 °C, valeur supérieure à 10°C. La réglementation n'est pas respectée.
2.b.
Le réglage n°2 satisfait-il à la réglementation ? On estimera combien
de temps la barquette doit rester dans la cellule de refroidissement
rapide pour atteindre une température de 10°C.
Au bout de 2 heures, la température lue sur la courbe C2 est voisine de 9 °C, valeur inférieure à 10°C. La réglementation est respectée.
La température de 10°C est atteinte au bout de 1,75 h ( 1 h 45 min d'après la courbe C2).
3. Un employé
affirme que la température de la barquette baisse de 5 % toutes les
minutes avec le réglage n°2. Expliquer pourquoi cette affirmation est
en contradiction avec la courbe C2.
temps ( minutes)
|
0
|
1
|
2
|
3
|
4
|
5
|
température (°C) calculée
|
63
|
63x0,95 ~60
|
60x0,95 ~57
|
57 x0,95 ~54
|
51,5
|
49
|
La courbe C2 indique que la température de 49°C est atteinte au bout de 0,25 h soit 15 minutes.
4. On admet que la
température baisse de 2 % toutes les minutes avec un réglage n°3.
Compléter les lignes 3, 4 et 5 de l'algorithme ci-dessous afin que ce
dernier détermine au bout de combien de temps la température de la
barquette sera inférieure à 10°C.
N <-- 0
T <--63
Tant que T > 10
Affecter à N la valeur N+1
Affecter à T la valeur 0,98 T
Fin de Tant que.
|
|
Partie B.
La température de la cellule de refroidissement rapide est réglée à 3°C.
Pour le réglage n°2, la température de la barquette est modélisée par
une fonction f, qui à tout temps ( en heure) associe la température de
la barquette en °C. Cette fonction est solution de l'équation
différentielle suivante : y' = -1,2(y-3) sur [0 ; +oo[.
1.a. Démontrer que cette équation s'écrit sous la forme (E) : y'+1,2 y = 3,6.
y' = -1,2y - 3 x(-1,2) ; y' = -1,2 y +3,6 ; y'+1,2 y = 3,6.
1.b . Déterminer les solutions de l'équation différentielle y' +1,2 y = 0 sur [0 ; +oo[.
y = A e-1,2t, avec A une constante.
1.c . Vérifier que la fonction constante t -->3 est une solution particulière de (E). En déduire les solutions de (E).
La dérivée d'une fonction constante est nulle.
1,2 x3 = 3,6.
Solutions de (E) : y = A e-1,2t +3.
1.d.
Expliquer pourquoi f(0) = 63. Déduire de ce qui précède une expression de f(t).
La température initiale d'une barquette est égale à 63°C.
f(0) = A e0 +3 = 63 d'où A +3=63 soit A = 60.
f(t) = 60 e-1,2t +3 sur [3 ; +oo[.
2. Donner la valeur arrondie à 10-2 de f(2). Interpréter.
f(2) = 60 e-2,4+3 ~8,44.
Au bout de 2 h de refroidissement la température de la barquette atteint 8,44 °C.
3. Déterminer la limite de la fonction f en plus l'infini. Interpréter.
Le teme en exponentielle tend vers zéro quand t tend vers plus l'infini.
f(t) tend vers3 quand t tens vers plus l'infini.
La température finale de la barquette est égale à celle de la cellule de refroidissement.
4. Avec un logiciel de calcul formel, on obtient 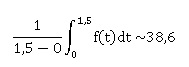 . Interpréter ce résultat. . Interpréter ce résultat.
La température moyenne de la barquette au cours des 90 premières minutes de refroidissement est de 30,8 °C.
5.
Pour le réglage n°1, la température de la barquette est modélisée par
une fonction g qui à tout temps en heure associe la température g(t) en
°C. Proposer une expression de g(t).
Les courbes ont la même allure : g(t) est de la forme de f(t).
La température initiale de la barquette est 63°C et la température finale 3°C.
La barquette se refroidit moins vite.
g(t) = 60 e-t +3.
|
|
. .
|
|