Loi
binomiale, loi normale, BTS groupe D 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1.
Partie A.
Une étude montre que :
60 % des scanographies effectuées concernent le cerveau, parmi
celles-ci 20 % détectent une tumeur.
90 % des autres scanographies effectuées ne détectent pas de tumeur.
On choisit un patient au hasard. On note C l'événement " le patient
fait une scanographie du cerveau" et T l'événement " le patient a une
tumeur".
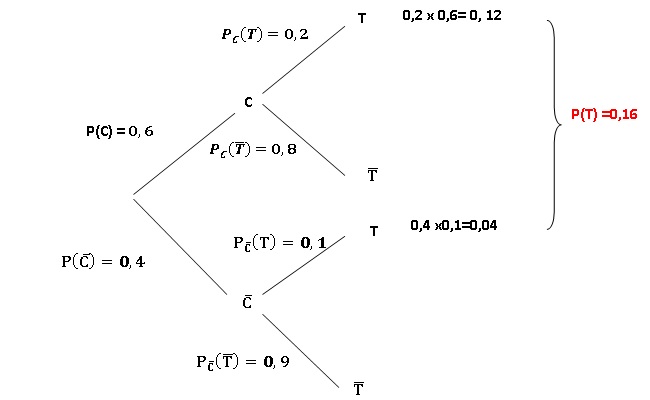
1. Compléter
l'arbre pondéré suivant.
2.
Montrer que la probabilité que le patient ait une tumeur est égale à
0,16.
3.
Le scanographe détecte une tumeur. Quelle est la probabilité que cette
tumeur soit détectée au cerveau ?
PT(C) =P(T n C) / P(T) = 0,12 / 0,16 = 0,75.
4.
Sur un échantillon de 40 patients atteints d'une tumeur au cerveau, un
médecin constate que 25 patients ont été guéris après un traitement
approprié.
a. Donner une estimation ponctuelle
f de la proportion inconnue de patients guéris d'une tumeur au cerveau
après un traitement approprié.
f = 25 / 40 = 0,625.
b. Estimer cette proportion par un
intervalle de confiance au seuil de 95 %.
1,96 [f (1-f) / n]½ =1,96[0,625 x0,375 / 40]½
=0,150.
Intervalle de confiance [0,625-0,15 ; 0,625 +0,15] soit [ 0,475 ;0,775 ].
Partie B.
Le délai d'attente en jours pour réaliser une scanographie suit une loi
exponentielle de paramètre l
et le délai d'attente moyen est de 10 jours.
1. Déterminer l.
l = 1
/ 10 = 0,1 jour-1.
2. Parmi les trois
représentations ci-dessous, une seule correspond à la densité de
probabilité de cette loi exponentielle. Indiquer laquelle, sans
justifier.
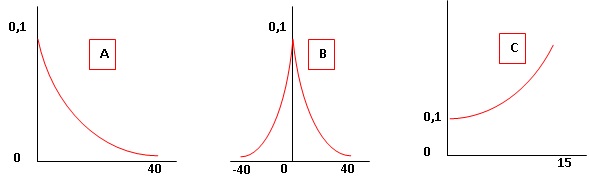
La représentation A est
correcte.
3. Déterminer la
probabilité, arrondie au millième, que le délai d'attente d'un patient
ne dépasse pas 8 jours.
P(T < 8) = 1-e-0,8
= 0,551.
|
|
|
|
|
Partie C.
QCM sans justification.
On admet que la probabilité que le délai d'attente d'un patient pour
une scanographie ne dépasse pas 8 jours est égale à 0,55.
On construit
aléatoirement un échantillon de 200 patients de l'hopital, qui se
voient prescrire une scanographie. On appelle X la variable aléatoire
égale au nombre de patients dont le délai d'attente ne dépasse pas 8
jours.
1. La variable X suit :
A. la loi binomiale de paramètres 200 et 0,55 ;(exact)
B. la loi normale de paramètres 200 et 0,55 ;
C. la loi exponentielle de paramètres 200 et 0,55.
2. La probabilité
que le quart de ces 200 patients ait un délai d'attente qui ne dépasse
pas 8 jours est égale à :
A. P(X < 8)
; B. P(X = 0,25) ; C. P(X =50). exact.
3. La probabilité
que moins de la moitié des 200 patients aient un délai d'attente qui ne
dépasse pas 8 jours est égale à :
A. 0,021 ; B. 0,088 ( exact)
; C. 0,932.
4. On admet que la loi suivie par X
peut être approchée par une loi normale. La représentation graphique de
cette loi est alors :
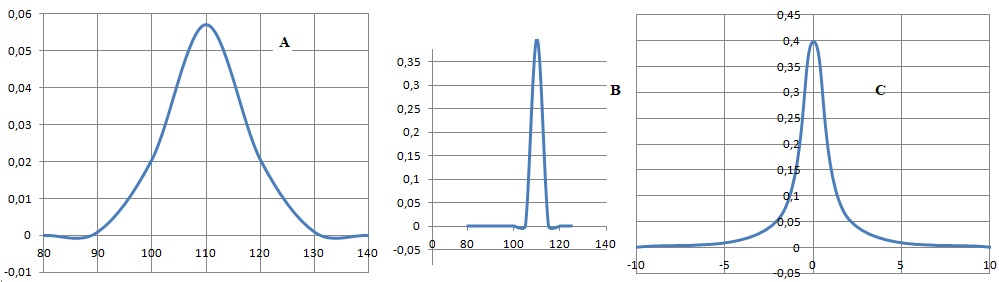
Représentation A.
|
|
. .
|
|