Loi
binomiale, loi normale, tests, BTS groupe C 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice 2 ( 10 points).
Partie 1. Loi binomiale.
Les pales sont contrôlées périodiquement. On a établi 4 classes de gravité des dommages.
Classe 4 : dégâts légers qui ne nécessite t ni intervention, ni arrêt.
Dans les trois autres cas, il y a intervention et arrêt.
Classe 3 : la pale est réparée sur place.
Classe 2 : la pale doit être démontée.
Classe 1 : changement des trois pales.
Dans 98,2 % des cas le technicien ne diagnostic aucun souci sur la pale ou bien seulement un dommage de classe 4.
Dans tous les autres cas, on dira que la pale est défaillante.
On désigne par X la variable aléatoire qui, à chaque inspection des 70
éoliennes, associe le nombre de pales nécessitant une intervention.
1. Justifier que X suit une loi binomiale B(210 ; 0,018).
Nombre total de pales : n=3 x70 = 210.
Les 210 tirages sont identiques, aléatoires, indépendants. Il y a
toujours deux issues possibles : X :" intervention "ou non intervention.
p(X) = 1-0,982 =0,018.
X suit la loi binomiale de paramètre n = 210, p = 0,018.
2. Calculer la probabilité qu'il n'y ait aucune pale nécessitant une intervention.
P(X=0) =(1- 0,018)210 =0,0221.
3. Calculer la probabilité qu'il y ait au plus 2 pales défaillantes.
p(X < 2 ) =P(X=0) + P(X=1) + P(X=2) =.0,2695.
4. Calculer le nombre moyen de pales nécessitant une intervention.
np = 210 x0,018=3,78. ( environ 4 pales).
On rappelle que :
Si X suit une loi binomiale de paramètres n et p avec n > 30 et
np(1-p) < 10, on peut approcher la loi binomiale par la loi de
Poisson P(l) où l = np.
5.a. Montrer que dans les conditions de l'exercice, une telle approximation est envisageable et déterminer la valeur de l.
n = 210 > 30 ; np(1-p) = 210 x0,982 x0,018 =3,7 < 10. l'approximation est envisageable.
l = n p = 210 x0,018 = 3,78.
5.b. On désigne par Z la variable aléatoire qui suit la loi de Poisson de paramètre l. Calculer P(Z < 2) et conclure.
P( Z < 2) =.0,272.
Valeur cohérente avec celle trouvée dans le cadre de la loi binomiale. (0,269).
Partie2. Loi normale.
Les éoliennes comportent un frein mécanique permettant d'immobiliser le
rotor au cours des opérations de maintenance. Une entreprise fabrique
des pièces de rechange pour ce frein. On admet que la variable
aléatoire Y qui, à chaque pièce de ce mécanisme, associe son diamètre
exprimé en mm, suit la loi normale d'zspérance m = 22 et d'écart type s = 0,025.
L'entreprise accepte une pièce si son diamètre appartient à l'intervalle [21,94 ; 22,06].
Quelle est la probabilité qu'une pièce prise au hasard dans la production soit refusée ?
P(Y < 21,94)=)0,0081975.
P(Y < 22,06)=)0,9918.
P(21,94 < Y < 22,06) = 0,9918-0,0081975=0,9836.
Probabilité de refus : 1 -0,9836 =0,0164.
|
|
Partie3. Test d'hypothèse.
Afin de vérifier le bon fonctionnement de la
machine, on prélève régulièrement dans la production des échantillons
de 100 pièces.
l'entreprise construit un test bilatéral au seuil de 5 %.
On appelle Z la variable aléatoire qui, à chaque échantillon de 100
pièces, associe le diamètre moyen des pièces de cet échantillon. le
nombre de pièces est assez important pour que l'on puisse assimiler ces
prélevements à des tirages avec remise.
Lorsque la machine est bien réglée, Z suit la loi normale de paramètre m et s0 = s / 10.
On chhoisit l'hypothèse H0 : "m = 22".
1. Donner l'hypothèse alternetive H1.
"m diffère de 22".
2. On admet que sous l'hypothèse H0, Z suit la loi normale de moyenne m et d'écart type s0. Déterminer h tel que :
P(22-h < Z < 22+h) = 0,95.
h = 1,96 s0 =1,96 x0,0025=0,0049.
3. Enoncer la règle de décision du test.
Dans un échantillon de 100 pièces, si la fréquence du diamètre despièces appartient à [21,995 ; 22,005 ],
l'hypothèse H0 est retenue avec un niveau de confiance de 95 %. Sinon H1 est retenue.
4. On prélève au hasard un échantillon de 100 pièces et on mesure leur diamètre.
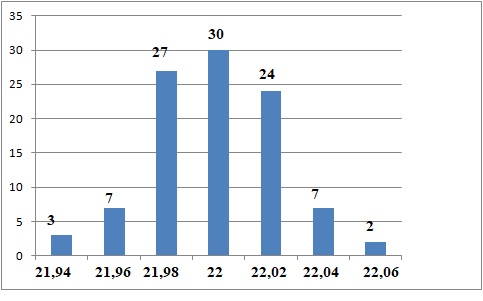
a.
En supposant que toutes les pièces d'une classe ont pour diamètre la
valeur centrale de cette classe, donner la moyenne des diamètres pour
cet échantillon.
(3 x21,94 +7 x21,96 +27 x21,98 +30 x22 +24 x22,02 +7 x22,04 +2 x22,06 ) / 100 = 21,9988 mm.
b. Peut-on accepter, au seuil de risque de 5 %, l'hypothèse selon laquelle la machine est bien réglée ?
21,9988 mm appartient à [21,995 ; 22,005 ],
l'hypothèse H0 ( machine bien réglée ) est retenue avec un niveau de confiance de 95 %. |
|
. .
|
|