Equation
différentielle, étude de fonctions, BTS groupe C 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice
1 ( 10 points).
La production électrique éolienne est en fort développement.
Partie 1. Modèle statistique.
Le
Grenelle de l'environnemen a fixé pour 2020 l'objectif suivant : 10 %
de notre électricité doit être fournie par l'énergie éolienne, soit une
puissance de 25 GW. On veut étudier si la progression actuelle
permettra de réaliser cet objectif.
Année
|
2010
|
2011
|
2012
|
2013
|
20145
|
2015
|
2016
|
Rang de l'année xi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Puissance (GW) yi
|
5,76
|
6,71
|
7,54
|
8,15
|
9,31
|
10,3
|
10,85
|
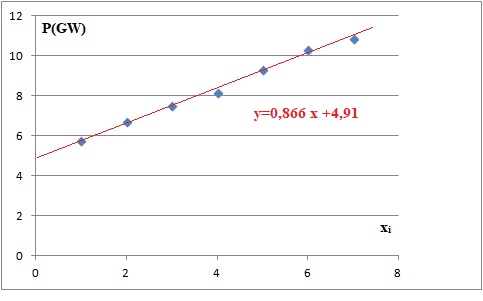
En admettant que la progression se confirme, étudier si l'objetif peut être atteint.
En 2020, x = 11 ; y = 0,866 x11 +4,91 = 14,43 GW.
Cette valeur est inférieure à 25 GW, l'objectif n'est pas atteint.
Partie2. Modèlisation de la puissance d'une éolienne.
Un parc éolien est constitué de 6 éoliennes de même type. Ces éoliennes
possèdent 3 pales et ont un diamètre de 100 m. Les pales commencent à
tourner lorsque le vent atteint une vitesse de 3 m /s.
1.
Lorsque l'éolienne atteint son plein régime, ses pales effectuent 16
tours par minute. Quelle est la vitesse en km / h à l'extrémité de la
pale ?
16 / 60 = 4 / 15 tour /s soit 4 / 15 x3,14x2 = 1,675 rad /s.
Vitesse à l'extrémité de la pale : 1,675 x 50 ~83,8 m /s ou 83,8 x3,6 = 301,6 km / h.
2.
La puissance P( kW) d'une éolienne , en fonction de la vitesse v du
vent ( m /s)est modélisée par la fonction P définie sur [3 ; +oo[ par :
P(v) = -55 +5110 / (2 +750 e-0,75v).
On donne : f(x)=1 / (2 +750 e-0,75x) ; la fonction dérivée f '(x) = 562,5 e-0,75 x / (2 +750 e-0,75x)2.
Intégration de P(v) entre 5 et 12 : 9872,1.
a. Calculer la puissance d'une éolienne si v = 3 m /s.
P(3) = -55 +5110 / (2 +750 e-2,25)~8,05 kW.
b. Etudier les variations de P(v) sur [3 ; +oo[.
f '(x) = 562,5 e-0,75 x / (2 +750 e-0,75x)2.
e-0,75 x et (2 +750 e-0,75x)2 sont positifs sur cet intervalle.
Donc P(v) est strictement croissante sur [3 ; +oo[.
Quand v tend vers plus l'infini, e-0,75v tend vers zéro et P(v) tend vers : -55 +5110 /2 =2500 kW.
En réalité une éolienne ne fonctionne plus au delà d'une certaine
vitesse du vent appelée vitesse de coupure. ( 20 m / s dans ce
cas).
c. Calculer la puissance d'une éolienne quand la vitesse de coupure est atteinte.
P(20) = -55 +5110 / (2 +750 e-15)=2499,7 kW.
d. Déterminer en
m/s, à l'unité près, la vitesse du vent à partir de laquelle la
puissance d'une éolienne est supérieure à 2000 kW.
2000 = -55 +5110 / (2 +750 e-0,75 v) ;
2055 =5110 / (2 +750 e-0,75 v) ;
2 +750 e-0,75 v=5110 / 2055~2,487.
e-0,75 v=(2,487 -2) / 750 ~6,488 10-4 ;
-0,75 v = ln(6,488 10-4 ) ~ -7,34
v = 9,78 ; v doit être supérieur ou égal à 10 m /s.
|
|
3.a. Calculer la puissance moyenne d'une éolienne lorsque la vitesse du vent varie entre 5 et 12 m /s.
Pmoy = Intégrale de P(v) entre 5 et 12 divisé par (12-5 )= 9872,1 / 7 ~1410,3 kW.
3.b. Estimer le nombre d'éoliennes de ce type nécessaire pour atteindre une production totale de 1000 MW.
Une éolienne produit en moyenne 1,41 MW.
Nombre d'éoliennes : 1000 / 1,41 ~709.
|
|
. .
|
|