Chauffe-eau
solaire, BTS EEC 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Schéma d'une installation de chauffe-eau solaire.
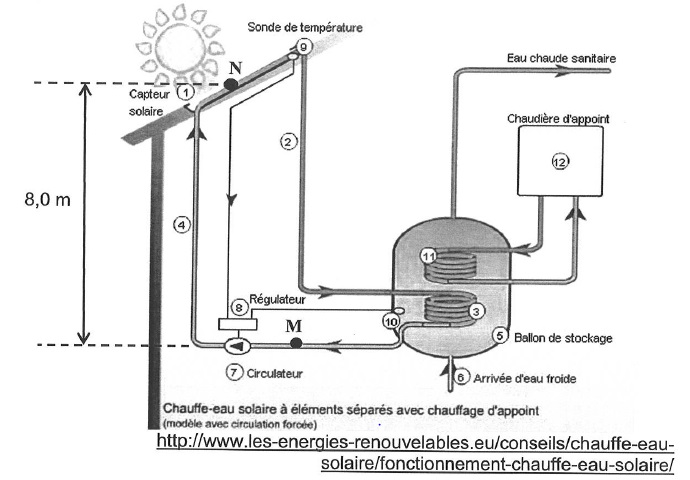
A. Chauffage de leau du ballon de stockage ( 7 points).
Capacité de remplissage du ballon : 200 L.
Capacité thermique massique de l'eau Ceau = 4,18 kJ kg-1 K-1.
A.1. Température de l'eau dans le ballon.
Surface du capteur solaire installé sur le toit : 3,5 m2. Le soleil fournit chaque jour une énergie égale à 4,80 kWh m-2. La température initiale de l'eau du ballon est de 15,0 °C.
1.1 Quelle est l'énergie thermique apportée chaque jour par le soleil au fluide caloporteur ?
4,80 x 3,5 = 16,8 kWh ou 16,8 x3600 = 6,048 104 kJ.
1.2.
En admettant que les pertes thermiques sont de l'ordre de 20 %, quelle
est l'énergie apportée sous forme de chaleur à l'eau, en une journée,
par le fluide caloporteur.
6;048 104 x 0,80 ~4,84 104 kJ.
1.3. Montrer que la température de l'eau atteint 73 °C en fin de journée.
Q = m Ceau Dq ; Dq = 4,84 104 /(200 x4,18) = 57,9 °C
Température finale de l'eau ; 15 + 57,9 = 72,9 ~73 °C.
1.4.
Après une nuit, la température de l'eau dans le ballon est d'environ 40
°C, ce qui correspond à des pertes thermiques de l'ordre de 7,7 kWh.
Citer le mode principal de transfert thermique à l'origine de ces
pertes.
Transfert thermique par conduction.
A.2. Amélioration énergétique du ballon avec l'utilisation de matériaux à changement de phase ( MCP).
Ces
matériaux sont contenus dans de petites billes en plastique,
directement au contact de l'eau du ballon. Lorsqu'un corps passe de
l'état solide à l'état liquide, il absorbe une certaine quantité
d'énergie et inversement lorsqu'il passe de l'état liquide à l'état
solide, il libère de l'énergie.
Caractéristiques du MCP utilisé :
température de fusion : Tf = 50 °C ; chaleur latente de fusion Lf = 189 kJ kg-1.
A.2.2. Compléter le schéma suivant en indiquant le nom des changements d'état corespondants.

A.2.3. A quelle température les MCP deviennent-ils efficaces ? Justifier.
A 50 °C, les MCP passent de l'état liquide à l'état solide et libèrent de l'énergie.
A.2.4. Pour une
efficacité optimale, on utilise 50 kg de MCP dans le ballon. Quelle
quantité d'énergie fournissent les MCP lors de leur changement d'état ?
50 x 189 = 9,45 103 kJ soit 9,45 103 / 3600 ~2,6 kWh.
A.2.5. En comparant cette valeur à celle des pertes thermiques, conclure quant à l'utilité des MCP dans le ballon.
Cette valeur correspond à 2,6 / 7,7 x100 ~34 % des pertes thermique
nocturnes. Les pertes thermiques nocturnes sont en parties compensées.
|
|
B. Coût de fonctionnement de la pompe du circuit du fluide caloporteur. ( 6 points).
Caractéristiques de la station solaire :
Pression de service : 2,5 bar ; pression de service maximale : 10 bar ;
contenance en fluide : 2,1 L ; débit préconisé : 72,4 kg h-1 ;
température de service maximale : 120 °C ; diamètre des tuyaux de liaison : 18,0 mm ; poids à vide : 37 kg.
Données : rcal = 1,035 103 kg m-3.
Equation de Bernoulli : ½ r (v2B-v2A) + (PB-PA) +rg(zB-zA) = Pu / Qv.
B.1. Etude du débit du fluide caloporteur.
B.1.1. Montrer que le débit volumique du fluide est d'environ 1,9 10-5 m3 s-1.
72,4 / (3 600 x 1,035 103) = 1,94 ~1,9 10-5 m3 s-1.
B.1.2. Calculer en m s-1, la vitesse du fluide dans les tuyaux.
Section s = 3,14 x(1,8 10-2)2 = 1,018 10-3 m2.
Vitesse = débit / section = 1,94 10-5 / (1,018 10-3 )=1,9 10-2 m s-1.
B.2. Détermination de la puissance utile de la pompe.
Un manomètre indique l'écart de pression entre les points M et N du circuit PN-PM = 2,5 bar.
La différence de hauteur entre les points M et N est 8,0 m.
B.2..1. Montrer que la puissance utile de la pompe est 6,3 W.
La vitesse du fluide est constante, les tuyaux ayant la même section.
L'équation de Bernoulli s'écrit : (PB-PA) +rg(zB-zA) = Pu / Qv.
2,5 105 +1035 x 9,81 x 8 = Pu / (1,94 10-5 ) ;
Pu = 3,31 105 x 1,94 10-5 = 6,43 ~6,4 W.
B.2.2. Sachant que le rendement de la pompe est de 93 %, quelle est la puissance électrique consommée par cette pompe ?
6,43 / 0,93 = 6,77 ~6,91 ~6,9 W.
B.2.3.
Un kWh coûte 0,1449 €. Quel est le prix de fonctionnement de la pompe
sur une année sachant qu'elle fonctionne 10 h par jour ? Commenter.
Durée de fonctionnement : 365 x 10 = 3650 heures.
Energie consommée : 6,91 *3650 ~2,5 104 Wh = 25 kWh..
Coût : 25 x 0,1449 ~3,6 €.
Un chauffe eau électrique de puissance 2000 W fonctionnant une heure par jour consomme : 2000 x 1 x365 =7,3 105 Wh = 730 kWh.
Coût : 730 x 0,1449 ~106 €.
Cette valeur est bien supérieure à la consommation de la pompe précédente.
|
|
C. Dépôt calcaire CaCO3 dans le ballon et protection contre la corosion.
C.1. Elimination du calcaire.
C.1.1. Expliquer pourquoi le calcaire, initialement dissout dans l'eau potable, peut se déposer dans le chauffe -eau.
La solubilité du calcaire dans l'eau diminue quand la température
augmente. Elle est presque divisée par 3 en passant de 0°C à 50 °C.
C.1.2. La dureté de l'eau potable est 25,0 °f. Calculer la concentration molaire de calcaire dissout dans cette eau.
1 °f correspond à 10 mg de calcaire disout par litre.
25 °f correspondent à 250 mg soit 0,25 g de calcaire dissout par litre.
Masse moaire du calcaire CaCO3 : M = 40,1 + 12 +3 x16 = 100,1 g / mol.
Concentration du calcaire dissout : 0,25 / 100,1 ~2,5 10-3 mol / L.
C.1.3. Montrer que
le calcaire peut se déposer dans le chauffe-eau.
A 50 °C, la solubilité du calcaire dans l'eau est égale à 2,0 10-3 mol / L, valeur inférieure à la concentration molaire du calcaire dans l'eau. Le calcaire se dépose dans le chauffe-eau.
C.1.4. Montrer que
la masse de calcaire pouvant se déposer dans le chauffe-eau en un
an est de 3,5 kg pour une consommation annuelle d'eau chaude à 50 °C,
de 70 m3.
(2,5 -2) 10-3 = 5 10-4 mol de calcaire se dépose par litre d'eau chaude.
Soit une masse : 5 10-4 x100,1 = 5,0 10-2 g par litre.
70 m3 = 7,0 104 litres ;
7,0 104 x5,0 10-2 = 3,5 103 g = 3,5 kg.
C.2. Protection contre la corrosion.
La carcasse en fer du ballon est émaillée et il y a contact de cette carcase avec une anode en zinc.
C.2.1. Comment se nomment ces deux types de protection ?
Protection anodique par le zinc.
Protection par recouvrement du fer par une couche d'émail.
C.2.2. Citer un métal qui pourrait remplacer le zinc.
Un métal plus réducteur que le fer peut convenir : magnésium.
C.2.3. Ecrure la demi-équation d'oxydation du zinc.
Zn(s) ---> Zn2+ + 2e-.
C.2.4
L'intensité du courant est estimée à 2,50 mA et on souhaite utilisée
une anode de zinc protégrant le ballon pendant 10 ans. Il faut
remplacer l'électrode lorsque 80 % de sa masse est consommée. Quelle
est la masse minimale de l'électrode en zinc ?
Durée : 10 ans = 10 x 365 x24 x3600 secondes = 3,15 108 s.
Quantité d'électricité Q = I t = 2,50 10-3 x 3,15 108 = 7,88 105 C.
Quantité de matière d'électron : n= 7,88 105 / 96500 = 8,17 mol.
Quantité de matière de zinc : 0,5 n = 4,085 mol.
Masse molaire du einc M(Zn) = 65,4 g / mol.
Masse de zinc m = 4,085 x 65,4 = 267 g.
267 / 0,8 = 334 g.
|
|