Mathématiques, Brevet Amérique du nord 2018

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1 . ( 14 points )
Le tableau ci-dessous est réalisé à l'aide d'un tableur.

	A	B	C	D
1		2014	2015	2016
2	Nombre d'abonnements Internet haut débit ( en millions)	22,855	22,63	22,238
3	Nombre d'abonnements Internet à très haut débit ( en millions)	3,113	4,237	5,446
4	Total ( en millions)	25,968	26,867	27,684

1. Combien d'abonnements Internet à très haut débit, en millions, ont été comptabilisés pour l'année 2016 ?
5,446 millions.
2.. Vérifier qu'en 2016, il y avait 817 000 abonnements Internet à haut débit et à très haut débit de plus qu'en 2015.
27,684-26,867 = 0,817 millions = 817 000.
3.Quelle formule a-t-on pu saisir dans la cellule B4 avant de la recopier vers la droite jusqu'à la cellule D4 ?
=Somme(B2:B3) ou bien = B2 +B3
4. En 2015, seulement 5,6 % des abonnements Internet à très haut débit utilisaient la fibre optique. Quel nombre d'abonnements Internet à très haut débit cela représentait-il ?
4,237 x5,6 / 100=0,2373 millions ou 237 272.

Exercice 2 ( 14 points)
.Le triangle ADE a pour dimensions : AD = 7 cm ; AE = 4,2 cm ; DE = 5,6 cm.
AF = 2,5 cm ; AB = AC = 9 cm.
Les droites (FG) et (DE) sont parallèles.

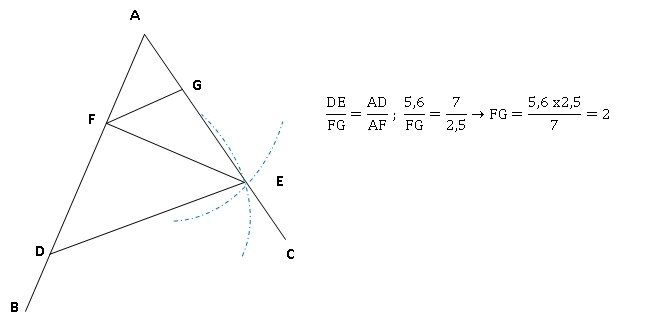
1. Réaliser la figure en vrai grandeur.
Tracer (AB) ; placer les points B et D sachant que AD = 7 cm et AB = 9 cm.
Pointe du compas en D, tracer un arc de cercle de rayon 5,6 cm.
Pointe du compas en A, tracer un arc de cercle de rayon 4,2 cm.
L'intersection des deux arcs définit le point E.
Tracer AE puis prolonger jusqu'au point C.
Placer le point G.
Tracer DE puis la parrallèle à DE passant par G.
2. Prouver que le triangle ADE est rectangle en E
AD² = 49 ; AE² + DE² = 4,2² +5,6² =49.
AD² =AE² + DE² ; d'après la réciproque du théorème de Pythagore, le triangle ADE est rectangle en E.
3. Calculer FG.
(FG) et (DE) sont parallèles, d'autre part (AC) et AB) sont sécantes.
A, G, E sont alignés, ainsi que AFD : le théorème de Thalès conduit à FG = 2 cm. ( voir calcul ci-dessus).

Exercice 3. ( 15 points).
Deux urnes contiennent des boules numérotée,s indicsernables au toucher.

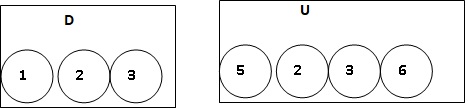
On forme un nombre entier à 2 chiffres en tirant au hasard une boule dans chaque urne.
Le chiffre des dizaines est le numéro de la boule issue de D. Le chiffre des unités est le numéro de la boule issue de U.
1. A t-on plus de chances de former un nombre pair que de former un nombre impair ?
On peut former : 12 ; 13 ; 15 ; 16 ; 22 ; 23 ; 25 ; 26 ; 32 ; 33 ; 35 ; 36.
6 nombres pairs et 6 nombres impairs parmi 12 nombres.
La probabilité de former un nombre pair est égale à celle de former un nombre impair.
2.a . Indiquer les nombres premiers que l'on peut former.
13 ; 23 ;
2.b . Montrer que la probabilité de former un nombre premier est 1 / 6.
2 cas favorables sur 12 cas possibles: 2 / 12 = 1 / 6.
3. Définir un événement dont la probabilité est 1 / 3.
44 cas favorables sur 12 cas possibles 4 / 12 = 1 / 3.
" Former un nombre qui soit un multiple de 3".
" Obtenir un entier dont la dizaine est 1".
" Obtenir un entier dont la dizaine est 2".

Exercice 4. ( 15 points).
Simon travaille sur un programme.

Script principal. Quand drapeau vert est cliqué aller à x =-200 y = 0 S'orienter à 90° ( on se dirige vers la droite) effacer tout mettre la taille du stylo à 1 mettre coté à 40 répéter 4 fois carré avancer de coté ajouter 20 à coté Fin répéter	Bloc carré Stylo en position écriture Répéter 4 fois avancer de coté tourner de 90° dans le sens anti-horaire Fin répéter Relever le stylo
	S'orienter à 90° signifie : on se dirige vers la droite.

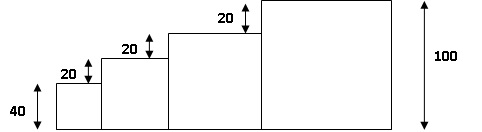
1. Il obtient le dessin ci-dessous : quelle est la longueur du côté du plus petit carré ? Quelle est la longueur du côté du plus grand carré ?

2. Dans le script principal, où peut-on insérer l'instruction " ajouter 2 à la taille du stylo" de façon à obtenir le dessin suivant ?

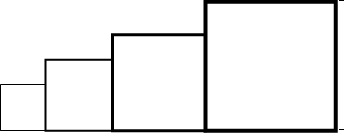
répéter 4 fois
    carré
    avancer de coté
    ajouter 20 à coté
ajouter 2 à la taille du stylo
Fin répéter.
3. On modifie le scripte principal.
.

Script principal. Quand drapeau vert est cliqué aller à x =-200 y = 0 S'orienter à 90° ( on se dirige vers la droite) effacer tout mettre la taille du stylo à 1 mettre coté à 40 répéter 4 fois carré avancer de coté +30 ajouter 20 à coté Fin répéter	Bloc carré Stylo en position écriture Répéter 4 fois avancer de coté tourner de 90° dans le sens anti-horaire Fin répéter Relever le stylo
	S'orienter à 90° signifie : on se dirige vers la droite.

Parmi les dessin ci-dessous, lequel obtient-on ?

On obtient le dessin n°3.

Exercice 5. ( 6 points )
Gaspard travaille avec un logiciel de géométrie dynamique pour construire une frise. Il construit un triangle ABC isocèle en C ( motif) 1) puis il a obtenu le losange ABCD ( motif 2).

1. Préciser une transformation permettant de complèter le motif 1 pour obtenir le motif 2.
Symétrie par rapport à la droite (AB).
2. Une fois le motif 2 construit, Gaspard a appliqué à plusieurs reprises une translation. Il obtient le motif ci-dessus.
Préciser de quelle trenslation il s'agit.
Translation qui transforme A en D et C en B.

Exercice 6. (16 points).
Madame Martin souhaite réaliser une terrasse en béton face à sa baie vitrée. Le sol de la terrasse doit être incliné. La terrasse a la forme d'un prisme droit dont la base est la quadrilatère ABCD et la hauteur le segment [CG].

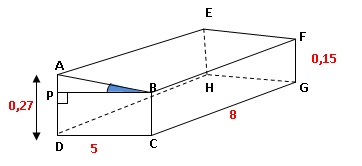
1. L'angle hachuré doit mesurer entre 1 et 5 °. Cette condition est telle vérifiée ?
tan ABP = AP / BP = (0,27-0,15) / 5 =0,024.
Cet angle mesure 1,37°. La condition est vérifiée.
2. Madame martin souhaite se faire livrer le béton.
Distance de l'entreprise à la maison : 23 km. Frais de livraison 5 € par km parcouru.
L'entreprise facture l'aller et le retour.
Prix du m³ de béton : 95 €.
Capacité maximale du camion : 6 m³.
Déterminer le montant de la facture.
Volume de béton = Aire ABCD fois hauteur CG.
V = (0,27 +0,15) x5 / 2 x 8 =8,4 m³. ( donc il faut deux camions).
Prix du béton : 8,4 x95 =798 €
Distancealler retour parcourue : 2 x2x23 = 92 km
Coût : 92 x5 = 460 €.
Montant de la facture : 460 +798 = 1258 €.

Exercice 7. ( 15 points ).
1. Développer et réduire l'expression A.
A = 2x(x-1)-4(x-1) =2x²-2x-4x+4 = 2x²-6x+4.
2. Montrer que -5 est solution de l'équation (2x+1) (x-2) = 63.
[2 (-5) +1] [-5-2] = -9 x (-7) = 63.
3. On considère la fonction f définie par f(x) = -3x+1,5.
Parmi les graphes ci-dessous, quel est celui qui représente cette fonction ? Justifier.

Le coefficient directeur de la droite est négatif.
f(0) = 1,5. La droite passe par le point de coordonnées ( 0 ; 1,5). Donc B.

Exercice 8. (6 points)
On considère la fenètre de téléchargement ci-dessous :
Téléchargé : 9,7 sur 115,2 M0 ( 1,3 Mo / s).
Si la vitesse de téléchargement reste constante, faudra t-il plus d'une minute et 25 s pour que le téléchargement se termine ?.
(115,2 -9,7) / 1,3 ~81 s ou 1 min 21 s soit moins d'une minute et 25 s.