Mathématiques,
Brevet des collèges Amérique du Sud 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
|
.
.
|
......
.....
|
Exercice 1. 12 points
Cet exercice est un questionnaire à choix multiples. Pour chaque question, une seule réponse est correcte.
Aucune justification n’est attendue.
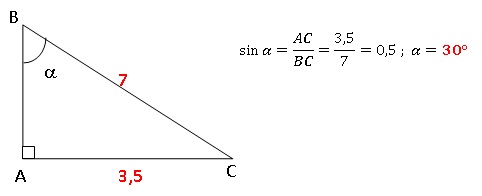
1. ABC est un triangle rectangle en A. AC = 3,5 cm et BC = 7 cm. La mesure de l’angle ABC est : 30 ; 45 ; 60.
2. Le triangle DEF est le symétrique du triangle ABC par rapport au point O. La mesure de l’angle DEF est : 35 ; 55 ; 65°.
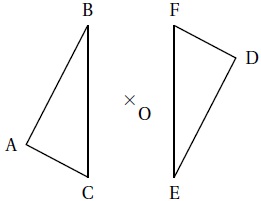
Les triangles sont symétriques par rapport à O.
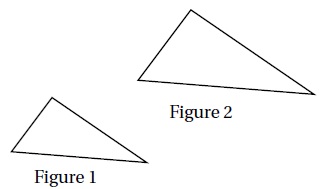
3. La transformation utilisée pour obtenir la figure 2 à partir de la figure 1 est une : translation, homothétie, rotation.
Exercice 2. 12 points.
Avant son déménagement, Hugo décide de se séparer de sa collection de
300 BD (bandes dessinées). 15% de ces BD sont trop abîmées pour être
vendues. Il les dépose à la déchèterie. À la braderie du village, il
vend ensuite trois cinquièmes de ce qu’il lui reste.
Combien rapporte-t-il de BD chez lui à la fin de la braderie?
Nombre de BD abimées : 300 x0,15 = 45.
Nombre de BD vendables : 300-45 = 255.
Nombre de BD vendues : 255 x3 / 5 =113.
Il en rapporte 255-153 = 102.
Exercice 3. 17 points.
Voici deux programmes de calcul :
Programme de calcul 1 : Soustraire 5 puis multiplier par 4
Programme de calcul 2 : Multiplier par 6 ; Soustraire 20 ; Soustraire le double du nombre de départ
1. a. Quel résultat obtient-on quand on applique le programme de calcul 1 au nombre 3 ?
3-5 = -2 puis -2 x4 = -8.
b. Quel résultat obtient-on quand on applique le programme de calcul 2 au nombre 3 ?
3 x6 = 18 ; 18 -20 = -2 ; -2-(2 x3) = --8
2. Démontrer qu’en choisissant le nombre −2, les deux programmes donnent le même résultat.
-2 -5 = -7 puis -7 x4 = -28.
-2 x6 = -12 ; -12 -20 = -32 ; -32-(2 x(-2) = -2832+4= -28.
3. On décide de réaliser davantage d’essais. Pour cela, on utilise un tableur et on obtient la copie d’écran suivante :
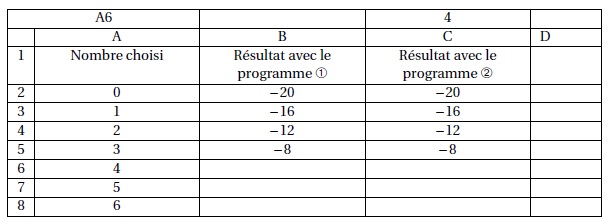
Quelle formule a-t-on pu saisir dans la cellule B2 avant de la recopier vers le bas, jusqu’à la cellule B5?
=A2*5-4
4. Les résultats
affichés dans les colonnes B et C sont égaux. Lucie pense alors que,
pour n’importe quel nombre choisi au départ, les deux programmes
donnent toujours le même résultat. Démontrer que Lucie a raison.
On appelle N le nombre de départ :
le programme 1 donne (N-5)x4= 4N-20.
Le programme 2 donne : 6N-20-2N = 4N-20.
|
|
|
|
Exercice 4. 18 points.
Valentin souhaite acheter un écran de télévision ultra HD (haute définition).
Pour un confort optimal, la taille de l’écran doit être adaptée aux dimensions de son salon.
Voici les caractéristiques du téléviseur que Valentin pense acheter :
Hauteur de l’écran 60 cm
Format de l’écran 16/9
Ultra HD Oui
Question : Valentin a-t-il fait un choix adapté?
Utiliser les informations ci-dessous et les caractéristiques du téléviseur pour répondre.
Toute trace de recherche,même incomplète, pourra être prise en compte dans la notation.
Information 1.
Distance écran-téléspectateur du salon de Valentin : 3,20 m.
Information 2. Format 16/9
Pour un écran au format 16/9, on a : Largeur =16 / 9 x hauteur.
Information 3. Graphique pour aider au choix de la taille de l’écran.
Largeur de l'écran : 16 / 9 x60 ~106,7 cm.
Diagonale de l'écran : (602 +106,72)½ ~122,4 cm.
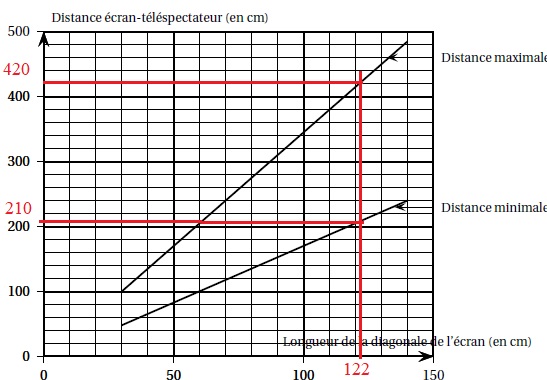
La distance écran- téléspectateur doit être comprise ensre 2,10 m et 4,20 m. Le choix est adapté.
|
....
|
Exercice 5. 17 points.
Dans
tout l’exercice, on étudie les performances réalisées par les athlètes
qui ont participé aux finales du 100 m masculin des Jeux Olympiques de
2016 et de 2012.
On donne ci-dessous des informations sur les temps mis par les athlètes pour parcourir 100 m.
Finale du 100 m aux Jeux Olympiques de 2016 :
Temps réalisés par tous les finalistes :
10,04 s ; 9,96 s ; 9,81 s ; 9,91 s ; 10,06 s ; 9,89 s ; 9,93 s ; 9,94 s
Finale du 100 m aux Jeux Olympiques de 2012 :
• nombre de finalistes . . . . . . . . . . . . . . . . . . . . . . . . . 8
• temps le plus long . . . . . . . . . . . . . . . . . . . . . . . . . 11,99 s
• étendue des temps . . . . . . . . . . . . . . . . . . . . . . . . . 2,36 s
• moyenne des temps . . . . . . . . . . . . . . . . . . . . . . . . . 10,01 s
• médiane des temps . . . . . . . . . . . . . . . . . . . . . . . . . 9,84 s
1. Quel est le temps du vainqueur de la finale en 2016 ?
9,81 s.
2. Lors de quelle finale la moyenne des temps pour effectuer 100 m est-elle la plus petite ?
Moyenne des temps 2016 : ( 10,04 +9,96 +9,81 +9,91 +10,06 +9,89 +9,93 +9,94) / 8~9,94 s.
La moyenne des temps 2016 est plus petite que celle des temps 2012.
3. Lors de quelle finale le meilleur temps a-t-il été réalisé?
Temps le plus court en 2012 : 11,99 -2,36 = 9,63 s.
Le meilleur temps a été réalisé en 2012.
4. L’affirmation suivante est-elle vraie ou fausse?
Affirmation : « Seulement trois athlètes ont mis moins de 10 s à parcourir les 100 m de la finale de 2012 »,
Médiane des temps 2012 : 9,84 s.
En 2012, 4 athlètes ont mis moins de 9,84 s. L'affirmation est fausse.
5. C’est lors de la finale de 2012 qu’il y a eu le plus d’athlètes ayant réussi à parcourir le 100 m en moins de 10 s.
Combien d’athlètes ont-ils réalisé un temps inférieur à 10 s lors de cette finale de 2012 ?
En 2016, 6 finalistes ont mis moins de 10 s.
En 2012, il y a eu plus de 6 finalistes ayant mis moins de 10 s. et le dernier a mis 11,99 s.
Réponse : 7.
Exercice 6. 12 points.
Léna et Youri travaillent sur un programme. Ils ont obtenu le dessin
suivant. Ils ont ensuite effacé une donnée par erreur dans le script
principal.
Voici les copies d’écran de leur travail :
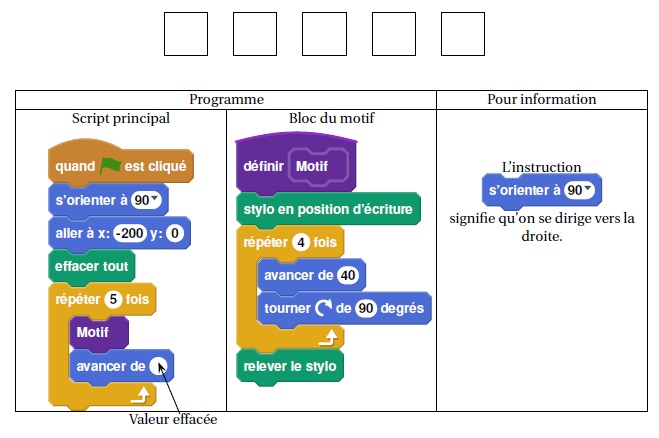
1. a. La valeur effacée dans le script principal était-elle 40 ou bien 60 ?
60.
b. Dessiner sur la copie ce qu’on aurait obtenu avec l’autre valeur.
2. Léna et Youri souhaitent maintenant obtenir un triangle équilatéral comme motif.
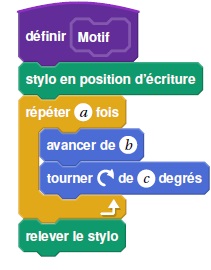
Afin d’obtenir un triangle équilatéral :
• par quelle valeur peut-on remplacer a ? 3.
• par quelle valeur peut-on remplacer b ? 40
• par quelle valeur peut-on remplacer c ? 120.
|
Exercice 7. 12 points.
En 2016 Marie-Amélie Le Fur a remporté la médaille d’or du 400 m aux Jeux Paralympiques de Rio.
Lors de la finale, elle a parcouru cette distance à la vitesse moyenne de 24,3 km/h en battant ainsi son propre record du monde
Noémie met 20 minutes à vélo pour parcourir les 7 km séparant le collège de sa maison.
Pour chacune des deux affirmations suivantes, dire en justifiant si elle est vraie ou fausse :
Affirmation 1 : « La vitesse moyenne de Noémie sur ces 7 km est supérieure à la vitesse moyenne de Marie-Amélie Le Fur lors de cette finale. »
Affirmation 2 : «Marie-Amélie Le Fur a couru le 400 m en moins d’une minute lors de cette finale. »
Vitesse de Marie-Amélie : 24,3 / 3,6 = 6,75 m / s.
400 m sont parcourus en 400 / 6,75 = 59,26 s.
L'affirmation 2 est vraie.
Vitesse de Noémie : 7000 / (20 x60) =5,83 m / s.
L'affirmation 1 est fausse.
|
|