Mathématiques,
Brevet Métropole 09 /2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
.
.
|
|
Exercice
1. 20 points
Partie 1.
On s’intéresse à une course réalisée au début de l’année 2018. Il y a
80 participants, dont 32 femmes et 48 hommes.
Les femmes portent des dossards rouges numérotés de 1 à 32. Les hommes
portent des dossards verts numérotés de 1 à 48.
Il existe donc un dossard n° 1 rouge pour une femme, et un dossard n° 1
vert pour un homme, et ainsi de suite ...
1. Quel est le
pourcentage de femmes participant à la course ?
32 / 80 = 0,4.
2. Un animateur
tire au hasard le dossard d’un participant pour remettre un prix de
consolation.
a. Soit l’évènement V : « Le dossard est vert ». Quelle est la
probabilité de l’évènement V ?
48 / 80 = 0,6.
b. Soit l’évènement
M : « Le numéro du dossard est un multiple de 10 ». Quelle est la
probabilité de l’évènement M ?
Nombre de multiples de 10 : 10 (femmes) ; 10 (hommes) ; 20 ( femmes) ;
20 ( hommes) ; 30 (femmes) ; 30 ( hommes) ; 40 (hommes).
7 / 80.
c. L’animateur
annonce que le numéro du dossard est un multiple de 10. Quelle est
alors la probabilité qu’il appartienne à une femme ?
3 cas favorables sur 7 possibilités : 3 / 7.
Partie 2.
À l’issue de la course, le classement est affiché. On s’intéresse aux
années de naissance des 20 premiers coureurs.
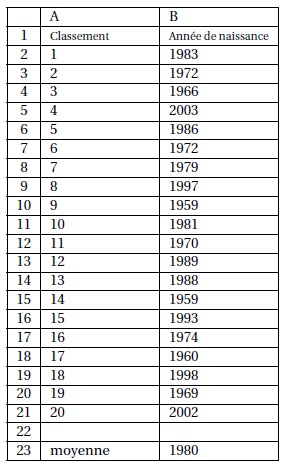
1. On a rangé les
années de naissance des coureurs
dans l’ordre croissant :
1959 1959 1960 1966 1969 1970 1972 1972 1974 1979
1981 1983 1986 1988 1989 1993 1997 1998 2002 2003
Donner la médiane de la série.
La médiane partage la série en deux parties contenant chacune le même
nombre de coureurs soit dix.
La médiane est choisie entre 1979 et 1981, 1980 par exemple.
2. La moyenne de la
série a été calculée dans la cellule B23. Quelle formule a été saisie
dans la cellule B23?
=MOYENNE(B1;B21)
3. Astrid remarque
que la moyenne et la médiane de cette série sont égales.
Est-ce le cas pour n’importe quelle autre série statistique ? Expliquer
votre réponse.
La moyenne et la médiane ne sont pas
toujours égales.
Soit la série 7 ; 8 ; 12 ; 14 ; 18.
la médiane est la valeur centrale 12.
La moyenne est ( 7 +8 +12 +14 +18) / 5 = 11,8.
Exercice 2. 11
points.
1. Le nombre 588 peut se décomposer sous la forme 588 = 22×3×72.
Quels sont ses diviseurs premiers, c’est-à-dire les nombres qui sont à
la fois des nombres premiers et des diviseurs de 588 ?
Les diviseurs de 22 sont 1 ; 2 ; 11 et 22
Les diviseurs de 72 sont : 1 ; 2 ; 3 ; 4 ; 6 ; 8 ; 9 ; 12 ; 18 ; 24 ;
36 ; 72.
Les nombres premiers diviseurs de 72 sont : 2 ; 3 ; 11.
2. a. Déterminer la
décomposition en facteurs premiers de 27 000 000.
27 000 000 = 26 x33 x56.
b. Quels sont ses
diviseurs premiers ?
Ces diviseurs premiers sont :2 ; 3
et 5.
3. Déterminer le plus petit nombre
entier positif impair qui admet trois diviseurs premiers différents.
Expliquer votre raisonnement.
Nombres premiers : 2 ; 3 ; 5 ; 7 ; 11 ; 13 .
Le nombre cherché étant pair, 2 est exclu comme diviseur.
3 x5 x7 =105.
Exercice 3 . 13
points.
Après un de ses entraînements de course à pied, Bob reçoit de la part
de son entraineur le récapitulatif de sa
course, reproduit ci-dessous.
Distance : 10,5 km ; durée : 1 h 03 min ; allure moyenne 6 min / km ;
calories : 851 ; gain altitude : 35 m.
L’allure moyenne du coureur est le quotient de la durée de la course
par la distance parcourue et s’exprime en min / km.
Exemple : si Bob met 18 min pour parcourir 3 km, son allure est de 6
min / km.
Exercice
4. 17 points.
Les
abeilles ouvrières font des allers-retours entre les fleurs et la ruche
pour transporter le nectar et le pollen des fleurs qu’elles stockent
dans la ruche.
1. Une abeille a
une masse moyenne de 100 mg et rapporte en moyenne 80 mg de charge
(nectar, pollen) à chaque voyage.
Un homme a une masse de 75 kg. S’il se chargeait proportionnellement à
sa masse, comme une abeille, quelle masse cet homme transporterait-il ?
Une abeille transporte une charge égale à 0,8 fois sa masse.
Un homme transporterait : 75 x 0,8 = 60 kg.
2. Quand elles
rentrent à la ruche, les abeilles déposent le nectar récolté dans des
alvéoles.
On considère que ces alvéoles ont la forme d’un prisme de 1,15 cm de
hauteur et dont la base est un hexagone d’aire 23 mm2
environ.
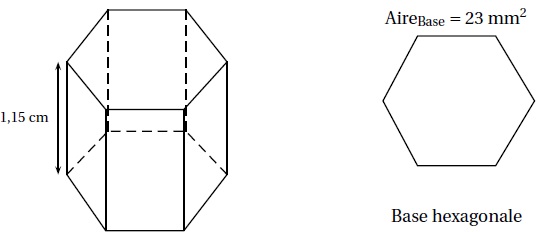
a. Vérifier que le
volume d’une alvéole de ruche est égal à 264,5 mm3.
Volume = aire de base x hauteur = 23 x 11,5 = 264,5 mm3.
b. L’abeille stocke le nectar dans
son jabot. Le jabot est une petite poche sous l’abdomen d’un volume de
6×10−5 litre. Combien de sorties au minimum l’abeille
doit-elle faire pour remplir une alvéole ? (rappel : 1 dm3 =
1 litre).
6×10−5 dm3 =60 mm3.
264,5 / 60 = 4,4 sorties.
3.
Le graphique ci-dessous présente la production française demiel en 2015
et 2016.
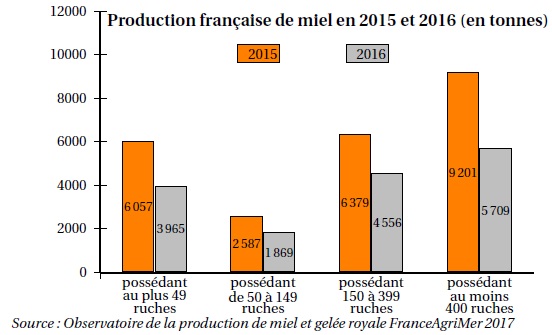
a. Calculer la
quantité totale de miel (en tonnes) récoltée en 2016.
3965 +1869 +4556 +5709 = 16 099 tonnes.
b. Sachant que la
quantité totale de miel récoltée en 2015 est de 24 224 tonnes, calculer
le pourcentage de baisse de la récolte de miel entre 2015 et 2016.
Baisse : 24 224 -16 099 = 8125 tonnes.
8125 / 24224 x100 = 33,5 %.
|
|
Exercice
5. 15 points.
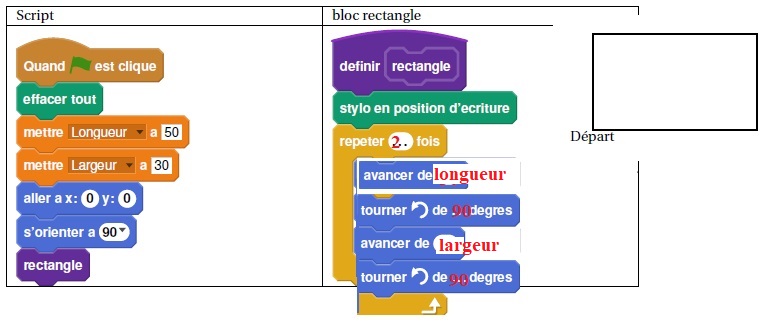
Sam a écrit le programme ci-dessous qui permet de tracer un rectangle.
Ce programme comporte deux variables (Longueur) et (Largeur) qui
représentent les dimensions du rectangle.
On rappelle que l’instruction s’orienter à 90 degres signifie que l’on
s’oriente vers la droite.
1. Compléter le bloc rectangle
ci-dessus avec des nombres et des variables pour que le script
fonctionne.
2. Lorsque l’on
exécute le programme, quelles sont les coordonnées du point d’arrivée
et dans quelle direction est-on orienté ?
Coordonnées (0 ; 0 ) ; on s'oriente vers la droite.
3. Sam a modifié
son script pour tracer également l’image du rectangle par l’homothétie
de centre le point de coordonnées (0; 0) et de rapport 1,3.
a. Compléter le
nouveau script de Sam donné ci-dessous afin d’obtenir la figure
ci-dessous. On recopiera et on complètera sur sa copie les lignes 9 et
10 ainsi que l’instruction manquante en ligne 11.
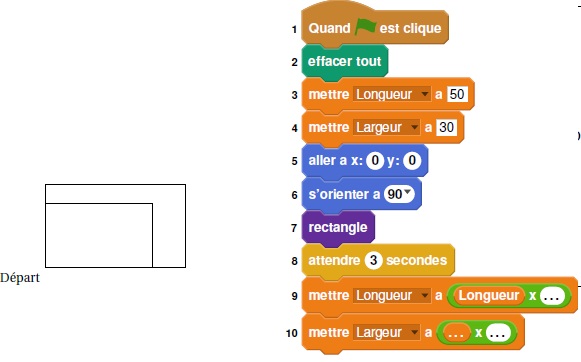
9 : Mettre longueur à longueur x 1,3.
10. Mettre largeur à largeur x1,3.
11. rectangle.
b. Sam exécute son
script. Quelles sont les nouvelles valeurs des variables Longueur et
Largeur à la fin de l’exécution du script ?
Longueur = 50 x1,3 = 65 ; largeur = 30 x1,3 = 39.
Exercice 6. 12 points.
La figure ci-dessous donne un schéma d’un programme de calcul.
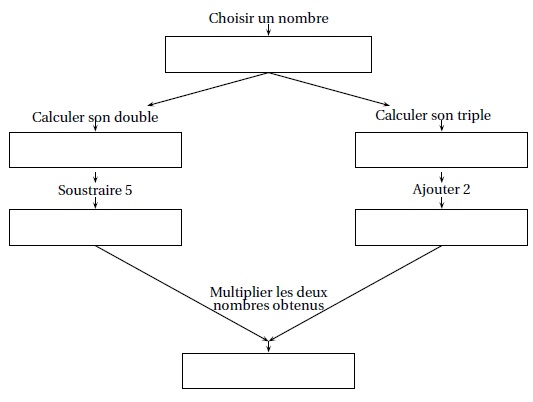
1. Si le nombre de
départ est 1, montrer que le résultat obtenu est −15.
1 x2 = 2 ; 2-5 = -3 ; 1 x3 = 3 ; 3+2 = 5 ; -3 x 5 = -15.
2. Si on choisit
un
nombre quelconque x comme nombre de départ, parmi les expressions
suivantes, quelle est celle qui donne le résultat obtenu par le
programme de calcul ? Justifier.
A = (x2 −5)×(3x +2) ; B
= (2x −5)×(3x +2) ; C = 2x −5×3x +2.
(2x-5) (3x+2).
3. Lily prétend
que l’expression D = (3x+2)2 −(x+7)(3x+2) donne les mêmes
résultats que l’expression B pour toutes les valeurs de x.
L’affirmation de Lily est-elle vraie? Justifier.
D = (3x+2) [ (3x+2) -(x+7)] = (3x+2) ( 2x-5). L'affirmation est vraie.
|
|
Exercice 7. 12 points.
Pour la course à pied en montagne, certains sportifs mesurent leur
performance par la vitesse ascensionnelle, notée Va.
Va est le quotient du dénivelé de la course, exprimé en
mètres, par la durée, exprimée en heure.
Par exemple : pour un dénivelé de 4 500 met une durée de parcours de 3
h : Va = 1500 m/h.
Rappel : le dénivelé de la course est la différence entre l’altitude à
l’arrivée et l’altitude au départ.
Un coureur de haut niveau souhaite atteindre une vitesse ascensionnelle
d’au moins 1 400 m/h lors de sa prochaine course.
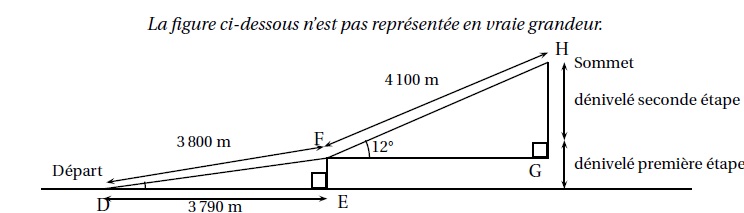
Le parcours se décompose en deux étapes :
• Première étape de 3 800 m pour un déplacement horizontal de 3 790 m.
• Seconde étape de 4,1 km avec un angle de pente d’environ 12°.
1. Vérifier que le
dénivelé de la première étape est environ 275,5 m.
Dans le triangle rectangle DEF :
EF2 = DF2 -DE2 = 38002
-37902 = 75900 ; EF = 275,5 m.
2. Quel est le
dénivelé de la seconde étape ?
sin 12 = GH / FH = GH / 4100 ; GH = 4100 x sin 12 =852,4 m.
3. Depuis le départ, le coureur met
48 minutes pour arriver au sommet. Le coureur atteint-il son objectif ?
Dénivelé total : 852,4 +275,5=1127,9 m.
48 minutes = 48 / 60 heure = 0,8 h.
Vitesse ascensionnelle : 1127.9 / 0,8 ~1410 m / h.
Cette valeur étant supérieure à 1400, l'objectif est atteint.
|
|