Mathématiques, Brevet centres étrangers 2018

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant soigneusement la réponse.
1. La récolte de la lavande débute lorsque les trois quarts des fleurs au moins sont fanées. Le producteur a cueilli un échantillon de lavande représenté
par le dessin ci-dessous.

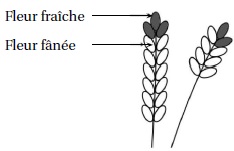
Affirmation 1 : la récolte peut commencer. Vrai.
Lavande de gauche : 3 fleurs sont fraiches et 12 sont fanées ; 12 / 15 = 0,8 > 0,75..
Lavande de droite : 2 fleurs sont fraiches et 7 sont fanées ; 7 / 9 ~ 0,78 > 0,75..
1. En informatique, on utilise comme unités de mesure les multiples de l’octet :
1 ko = 10³ octets,1 Mo = 10⁶ octets,1 Go = 10⁹ octets.
Contenu du disque dur externe :
• 1 000 photos de 900 ko chacune :
• 65 vidéos de 700 Mo chacune.
Capacité de l’ordinateur : 250 Go
Espace utilisé : 200 Go
Espace libre 50 Go.
Affirmation 2 : le transfert de la totalité du contenu du disque dur externe vers l’ordinateur n’est pas possible. Faux.
Contenu du disque dur externe : 1000 x 0,900 + 65 x700 =46 400 Mo =46,4 Go < 50 Go.
2. On considère le programme de calcul ci-dessous :
Choisir un nombre;
Ajouter 5 ;
Multiplier le résultat obtenu par 2 ;
Soustraire 9.
Affirmation 3 : ce programme donne pour résultat la somme de 1 et du double du nombre choisi.Vrai.
On appelle x le nombre choisi : 2(x+5)-9 =2x +10-9 = 2x +1.

Exercice 2 .
Les réponses aux questions de cet exercice seront lues sur la graphique suivant.
Celui-ci représente le profil d’une course à pied qui se déroule sur l’île de la Réunion (ce graphique exprime l’altitude en fonction de la distance parcourue par les coureurs), Aucune justification n’est attendue pour les questions 1 à 4.

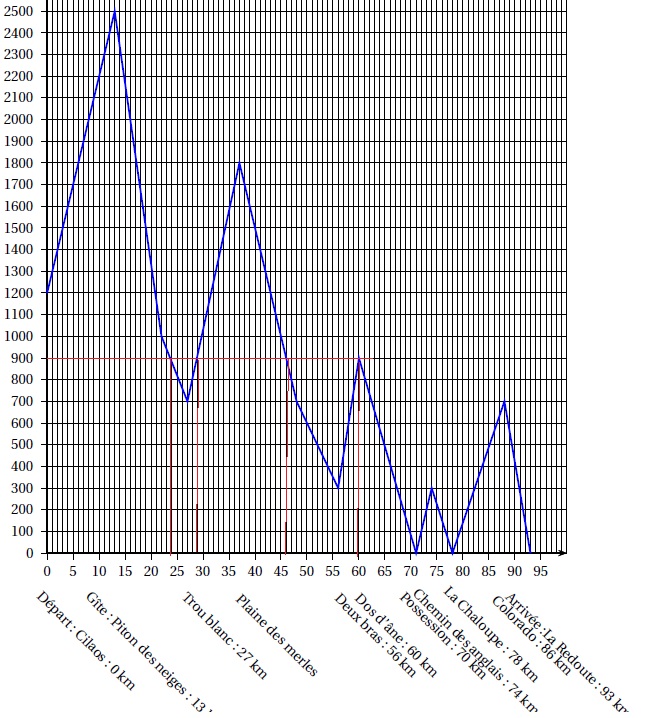
1. Quelle est la distance parcourue par un coureur, en kilomètres, lorsqu’il arrive au sommet de la plaine de 5 merles ?
37 km.
2. Quelle est l’altitude atteinte, en mètres, au gîte du Piton des neiges ?
2500 m
3. Quel est le nom du sommet situé à 900 mètres d’altitude ?
Dos d'âne.
4. À quelle(s) distance(s) du départ un coureur atteindra-t-il 1 900 m d’altitude?
7 et 18 km.
5. Le dénivelé positif se calcule uniquement dans les montées ; pour chaque montée, il est égal à la différence entre l’altitude la plus haute et l’altitude la plus basse.
a. Calculer le dénivelé positif entre Cilaos et le gîte du Piton des neiges.
2500-1200 = 1300 m.
b. Montrer que le dénivelé positif total de cette course est 4 000 m.
1300 + (1800-700) + (900-300) +(300-0) +(700-0) = 4000 m.
6. Maëlle a effectué sa course à une vitesse moyenne de 7 km/h et Line a mis 13 h 20 min pour passer la ligne d’arrivée.
Laquelle de ces deux sportives est arrivée en premier ?
Durée de la course de Maélle : 93 / 7 ~13,29 h soit 13 h 17 min.
Maëlle est arrivée avant Line.

Exercice 3.
Thomas possède une montre qu’il compose en assemblant des cadrans et des bracelets de plusieurs couleurs. Pour cela, Il dispose de :
• deux cadrans : un rouge et un jaune ; • quatre bracelets : un rouge, un jaune, un vert et un noir.
1. Combien y a-t-il d’assemblages possibles ?
4 x2 = 8 assemblages posibles.
Il choisit au hasard un cadran et un bracelet pour composer sa montre.
2. Déterminer la probabilité d’obtenir une montre toute rouge.
1 assemblage favorable sur 8 possibles : 1 / 8 = 0,125.
3. Déterminer la probabilité d’obtenir une montre d’une seule couleur.
Cadran et bracelet rouges ; cadran et bracelet jaunes.
2 cas favorables sur 8 possibles : 2 / 8 = 1 /4 = 0,25.
4. Déterminer la probabilité d’avoir une montre de deux couleurs.
Cadran rouge, bracelet jaune ; Cadran rouge, bracelet vert ; Cadran rouge, bracelet noir ;
Cadran jaune, bracelet rouge ; Cadran jaune, bracelet vert ; Cadran jaune, bracelet noir.
6 cas favorables sur 8 possibles ; 6 /8 = 3 /4 = 0,75.

Exercice 4.
Chaque été, Jean exploite son marais salant sur l’île de Ré, situé dans l’océan Atlantique, près de La Rochelle.
Son marais se compose de carreaux (carrés de 4 m de côté) dans lesquels se récolte le sel.
Partie A. Le gros sel
Chaque jour, il récolte du gros sel sur 25 carreaux. Le premier jour, afin de prévoir sa production, il relève la masse en kilogramme de chaque tas de gros sel produit par carreau.
Voici la série statistique obtenue :
34−−39−−31−−45−−40−−32−−36−−45−−42−−34−−30−−48−−43--32−−39−−40−42−−38−−46−−31−−38−−43−−37−−47
1. Calculer l’étendue de cette série statistique.
Ranger la série par ordre croissant :
30 ; 31 ; 31 ; 32 ; 32 ; 33 ; 34 ; 34 ; 36 ; 37 ; 38 ; 38 ; 39 ; 39 ; 40 ; 40 ; 42 ; 42 ; 43 ; 43 ; 45 ; 45 ; 46 ; 47 ; 48.
Plus ghrande valeur - plus petite valeur = 48-30 = 18.
2. Déterminer la médiane de cette série statistique et interpréter le résultat.
La série compte 25 données.
La médiane est la 13^ème donnée soit 39 kg.
3. Calculer la masse moyenne en kg des tas de gros sel pour ce premier jour.
Faire la somme et diviser par 25 : 965 / 25 = 38,6 kg.
Partie B. La fleur de sel
La fleur de sel est la mince couche de cristaux blancs qui se forme et affleure la surface des marais salants. Chaque soir, Jean cueille la fleur de sel à la surface des carreaux. Pour transporter sa récolte, il utilise une brouette comme sur le schéma ci-dessous.

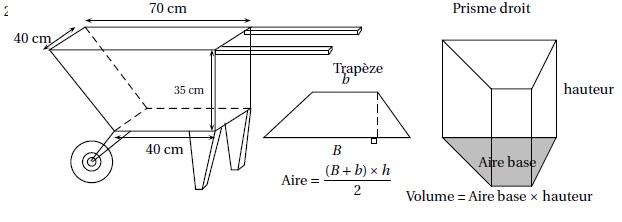
1. Montrer que cette brouette a un volume de 77 litres.
Aire de base : (40 +70) x35 / 2 = 1925 cm² = 19,25 dm².
Hauteur : 40 cm = 4 dm.
Volume : 19,25 x 4 = 77 dm³ = 77 litres.
2. Sachant que 1 litre de fleur de sel pèse 900 grammes, calculer la masse en kg du contenu d’une brouette remplie de fleur de sel.
77 x 0,900 = 69,3 kg.

Exercice 5.
Sur une facture de gaz, le montant à payer tient compte de l’abonnement annuel et du prix correspondant au nombre de kilowattheures (kWh) consommés.
Deux fournisseurs de gaz proposent les tarifs suivants :
Tarif A : prix du kWh(en (€) : 0,0609 ; Abonnement annuel 202,43 €.
Tarif B : prix du kWh(en (€) : 0,0574 ; Abonnement annuel 258,39 €
En 2016, la famille de Romane a consommé 17 500 kWh. Le montant annuel de la facture de gaz correspondant était de 1 268,18 €.
1. Quel est le tarif souscrit par cette famille ? Depuis 2017, cette famille diminue sa consommation de gaz par des gestes simples (baisser le chauffage de quelques degrés, mettre un couvercle sur la casserole d’eau pour la porter à ébullition, réduire le temps sous l’eau dans la douche, etc.).
Hypothèse A : 0,0609 x 17500 +202,43 = 1268,18.
Le tarif A a été souscrit.
2. En 2017, cette famille a gardé le même fournisseur de gaz, mais sa consommation en kWh a diminué de 20% par rapport à celle de 2016.
a. Déterminer le nombre de kWh consommés en 2017.
17500 x 0,80 = 14 000 kWh.
b. Quel est lemontant des économies réalisées par la famille de Romane entre 2016 et 2017 ?
3500 x 0,0609 = 213,15 €.
3. On souhaite déterminer la consommation maximale assurant que le tarif A est le plus avantageux.
Pour cela :
• on note x le nombre de kWh consommés sur l’année.
• on modélise les tarifs A et B respectivement par les fonctions f et g :
f (x) = 0,0609x +202,43 et g (x) = 0,0574x +258,39.
a. Quelles sont la nature et la représentation graphique de ces fonctions ?
Ce sont des fonctions affines dont les représentations graphiques sont des droites ne passant pas par l'origine.
b. Résoudre l’inéquation : f (x) < g (x).
0,0609x +202,43 < 0,0574x +258,39.
(0,0609-0,0574) x < 258,39 -202,43 ;
0,0035 x < 55,96 ;
x < 55,96 / 0,0035 ; x < 15 989.
c. En déduire une valeur approchée au kWh près de la consommation maximale pour laquelle le tarif A est le plus avantageux.
Le tarif A est le plus avantageux pour une consommation inférieure à 15 939 kWh.

Exercice 6.
Le maraîchage est l’activité professionnelle qui consiste à cultiver les légumes, certains fruits, fleurs ou plantes aromatiques.
Afin de diminuer la pénibilité des travaux de maraîchage, un agriculteur a acquis un robot électrique pour effectuer le désherbage de ses cultures.
Partie A. Parcours du robot
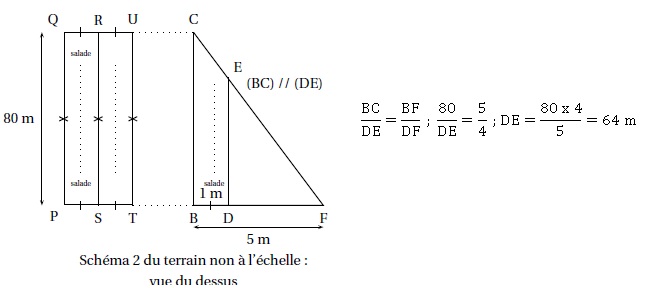
Le robot doit parcourir 49 allées parallèles écartés de 1 m, représentées sur le schéma ci-dessous.
Les 48 premières allées, situées dans une parcelle rectangulaire, mesurent 80 m de long :
• la 1^ère allée est [PQ] ;
• la 2^e allée est [RS] ;
• la 3^e allée est [TU] ;
• les allées 4 à 47 ne sont pas représentées ;
• la 48^e allée est [CB].
La 49^e (dernière allée) [DE] est située dans une parcelle triangulaire.
Montrer que la longueur de la dernière allée est DE = 64 m.
BC et DE sont parallèles. Utiliser la propriété de Thalès.

Partie B. Programme de déplacement du robot
On souhaite programmer le déplacement du robot du point P au point E. Le script ci-dessous, réalisé sous Scratch, est incomplet. Toutes les allées sont parcourues une seule fois. L’image« Robot »correspond au résultat attendu lorsque le drapeau vert est cliqué.
On rappelle que l’instruction s’orienter à 0 degrés signifie que le robot se dirige vers le haut.

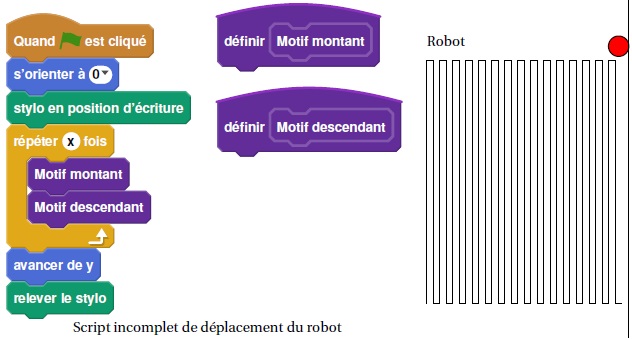
Les longueurs doivent être indiquées en mètres.
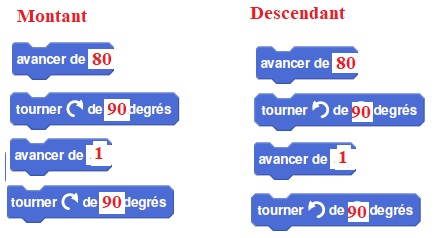
1. Le nouveau bloc «Motifmontant » doit reproduire un déplacement du type P-Q-R et positionner le robot prêt à réaliser le motif suivant. Écrire une succession de 4 blocs permettant de définir : «Motifmontant ».
2. Le nouveau bloc «Motif descendant » doit reproduire un déplacement du type R-S-T et positionner le robot prêt à réaliser le motif suivant. Quelle(s) modification(s)suffit-il d’apporter au bloc «Motifmontant » pour obtenir le bloc «Motif descendant » ?

3. Quelles valeurs faut-il donner à x et à y dans le script principal pour que le programme de déplacement du robot donne le résultat attendu.
48 / 2 = 24 ; x = 24.
La dernière longueur y mesure 64 m.