Mathématiques, brevet des collèges Nlle Calédonie 2018

Mathématiques, Brevet des collèges Nlle Calédonie 2018.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

......

.....

Exercice 1. 12 points
Cet exercice est un questionnaire à choix multiples. Pour chaque question, une seule réponse est correcte.
Aucune justification n’est attendue.
1 . La forme développée et réduite de (2x+5)(x-2) est : 2x²-10 ; 2x² +9x +10 ; 2x² +x-10.
2x² -4x +5x -10 = 2x²+x-10. Réponse C.
2.

Coté adjacent / hypothènuse = AB / BC = 4 / 5.

3. Lorsque j'ajoute deux multiple de 7, j'obtiens toujours :
un multiple de 49 ; un multiple de 14 ; un multiple de 7.
7 a + 7 b = 7 (a+b) avec a et b entier naturel non nuls.
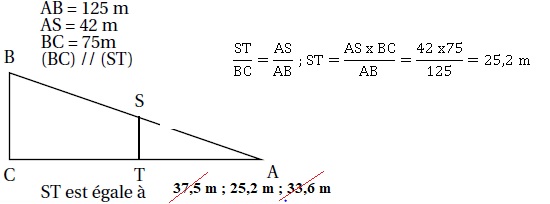
4.

Exercice 2. 12 points.
À un stand d’une kermesse, on fait tourner une roue pour gagner un lot (un jouet, une casquette ou des bonbons).
Une flèche permet de désigner le secteur gagnant sur la roue.
On admet que chaque secteur a autant de chance d’être désigné.

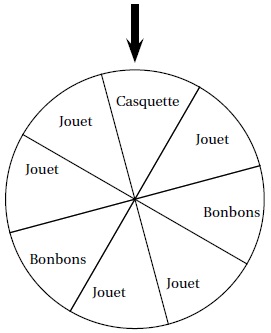
1. a. Quelle est la probabilité de l’évènement « on gagne des bonbons » ?
2 cas favorables sur 8 cas possibles : 2 / 8 = 1 / 4 = 0,25.
b. Définir par une phrase l’évènement contraire de l’évènement « on gagne des bonbons ».
" on gagne un lot qui n'est pas des bonbons".
" on gagne une casquette ou des jouets".
c. Quelle est la probabilité de l’évènement défini au 1. b. ?
1 -0,25 = 0,75.
2. Soit l’évènement « on gagne une casquette ou des bonbons ».
Quelle est la probabilité de cet évènement ?
3 cas favorables sur 8 cas possibles : 3 / 8 = 0,375.

.
.

Exercice 3. 18 points.
1. Décomposer les nombres 162 et 108 en produits de facteurs premiers.
162 = 2 x 3⁴ ; 108 = 2²x3³.
2. Déterminer deux diviseurs communs aux nombres 162 et 108 plus grands que 10.
18 ; 27 ; 54.
3. Un snack vend des barquettes composées de nems et de samossas.
Le cuisinier a préparé 162 nems et 108 samossas.
Dans chaque barquette :
— le nombre de nems doit être le même.
— le nombre de samossas doit être le même,
Tous les nems et tous les samossas doivent être utilisés.
a. Le cuisiner peut-il réaliser 36 barquettes ?
Non, 36 n'est pas un diviseur commun à 162 et 108.
b. Quel nombre maximal de barquettes pourra-t-il réaliser ?
Le plus grand commun diviseur à 162 et 108 est 2 x3³ = 54.
Il peut réaliser 54 barquettes contenant chacune 3 nems et 2 samosas.

...

Exercice 4. 16 points.
On étudie les performances de deux nageurs (nageur 1 et nageur 2).
La distance parcourue par le nageur 1 en fonction du temps est donnée par le graphique ci-dessous.

1. Répondre aux questions suivantes par lecture graphique. Aucune justification n’est demandée.
a. Quelle est la distance totale parcourue lors de cette course par le nageur 1?
2000 m.
b. En combien de temps le nageur 1 a-t-il parcouru les 200 premiers mètres ?
5 minutes.
2. Y a-t-il proportionnalité entre la distance parcourue et le temps sur l’ensemble de la course? Justifier.
Non, la courbe n'est pas une droite passant par l'origine.
3. Montrer que la vitesse moyenne du nageur 1 sur l’ensemble de la course est d’environ 44 m / min.
2000 m parcourus en 45 minutes : 2000 / 45 ~ 44m / min.
4. On suppose maintenant que le nageur 2 progresse à vitesse constante. La fonction f définie par f (x) = 50x représente la distance qu’il parcourt en fonction du temps x.
a. Calculer l’image de 10 par f .
f(10) = 50 *10 = 500 m.
b. Calculer f (30).
5. Les nageurs 1 et 2 sont partis en même temps,
a. Lequel est en tête au bout de 10 min? Justifier.
Le nageur 1 a parcouru 400 m en 10 minutes.
Le nageur 2 a parcouru 50 *10 = 500 m en 10 minutes. Celui-ci est en tête.
b. Lequel est en tête au bout de 30 min? Justifier.
Le nageur 1 a parcouru 1600 m en 30 minutes.
Le nageur 2 a parcouru 50 *30 = 1500 m en 30 minutes.
Le nageur 1 est en tête.

....

Exercice 5. 8 points.
Lors de son déménagement, Allan doit transporter son réfrigérateur dans un camion, Pour l’introduire dans le camion, Allan le pose sur le bord comme indiqué sur la figure. Le schéma n’est pas à l’échelle.

Allan pourra-t-il redresser le réfrigérateur en position verticale pour le rentrer dans le camion sans bouger le point d’appui A? Justifier.
AC² = AB² +BC² = 59² +198² =42 685 ; AC =206,6 cm = 2,066 m.
Cette valeur étant supérieure à 2,05 m, le réfrigérateur ne passe pas.

Exercice 6 : 17 points
L’annexe 1 (à la fin) donne un tableau concernant les états et territoires de la Mélanésie.
1. Compléter les colonnes B et C du tableau dans l’annexe 1. Arrondir les fréquences au dixième.

2. Le tableau a été construit avec un tableur.
Quelle formule peut-on saisir pour compléter la cellule B7 du tableau?
=SOMME(B2:B6)
L’annexe 2 donne la répartition des superficies des différents territoires et états de la Mélanésie.
3. Compléter la colonne des angles dans le tableau de l’annexe 2.
4. Compléter le diagramme semi-circulaire dans l’annexe 2 en utilisant les données du tableau.

18333 / 550560 x180 ~ 6 degrés.
12281 / 550560 x180 ~ 4 degrés.

Exercice 7. 8 points.
Pour chacune des affirmations suivantes, indiquer si elle est VRAIE ou FAUSSE et justifier la réponse.
Affirmation 1 : l’aire de la partie grise de la figure ci-dessous est 36−x². Faux.

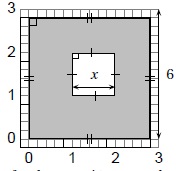
Aire du carré central : x² ;
Côté du carré grisé : 15 petits carreaux correspondent à 6 unités.
14 x6 / 15 = 5,6 unités.
Aire de ce carré : 5,6².
Aire de la partie grisée : 5,6² -x².
Affirmation 2 : le chiffré 8 est écrit 20 fois lorsque j’écris tous les nombres entiers de 1 à 100. Vrai.
8 ; 18 ; 28 ; 38 ; 48 ; 58 ; 68 ; 78 ; 80 ; 81 ; 82 ; 83 ; 84 ; 85 ; 86 ; 87 ; 88 ; 89 ; 98. Le chiffre 8 est écrit 20 fois.

Exerccice 8. 9 points.
On exécute le script 1 ci-dessous.
Représenter dans l’annexe 1 le chemin parcouru par le chat.

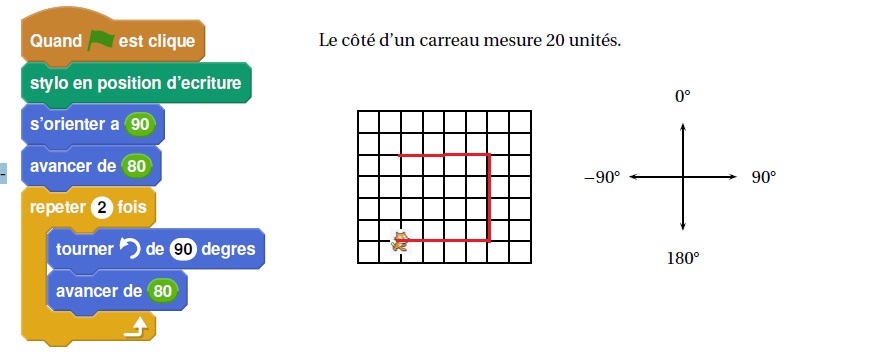
2. a. Indiquer sur la copie le numéro du dessin correspondant au script 2 ci-dessous.

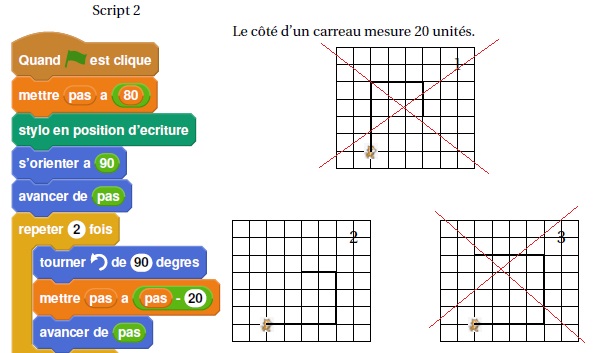
b. On souhaite modifier le script 2 pour parcourir le chemin suivant :

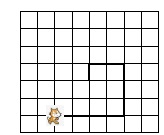
Quelle(s) modification(s) peut-on apporter au script 2 pour parcourir ce chemin?
Répéter 3 fois.

menu