Mathématiques, géométrie, suites, Bac S Amérique du Nord 2018

Mathématiques, géométrie, suites, Bac S Amérique du Nord 2018 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
	. .
	Exercice 3. ( 5 pts). On se place dans l'espace muni d'un repère orthonormé dont l'origine est le point A. On considère les points B(10 ; -8 ; 2) ; C(-1 ; -8 ; 5) et D(14 ; 4 ; 8). 1.a. Déterminer un système d'équations paramétriques de chacune des droites (AB) et (CD). b. Vérifier que ces droites ne sont pas coplanaires. Equations paramétriques de (AB) : x = 5t ; y = -4t ; z = t avec t réel. Equations paramétriques de (CD) : x = 5k+x_C ; y = 4k +y_C ; z = k+z_C avec k réel. x = 5k-1 ; y = 4k-8 ; z = k+5. Les droites (AB et (CD) sont-elles sécantes ? Hypothèse : elles sont sécantes. 5t = 5k-1 soit t = k-0,2. -4t = 4k-8 ; t = -k+2 t = k+5. Ces trois lignes sont incompatibles. L'hypothèse est fausse. Les droites ne sont pas sécantes. N'étant ni sécantes, ni parallèles, elles ne sont pas coplanaires. 2. On considère le point I de la droite (AB) d'abscisse 5 et le point J de la droite (CD) d'abscisse 4. a. Déterminer les coordonnées des points I et J et en déduire la distance IJ. 5 = 5t ; t =1 ; y_I = -4 ; z_I =1. Donc I( 5 ; -4 ; 1). 4 = 5k-1 ; k = 1 ; y_J= -4 ; z_J = 6. Donc J(4 ; -4 ; 6). IJ² =(4-5)² +(-4+4)²+(6-1)² = 26 ; IJ = 26^½. b. Démontrer que la droite (IJ) est perpendiculaire aux droites (AB) et (CD). La droite (IJ) est appelée perpendiculaire commune aux droites (AB) et (CD). 3. Sur le schéma ci-dessous on a représenté les droites (AB) et (CD), les points I et J, et la droite D parallèle à la droite (CD) passsant par I. On considère un point M de la droite (AB) distinct de I et un point M' de la droite (CD) distinct du point J. 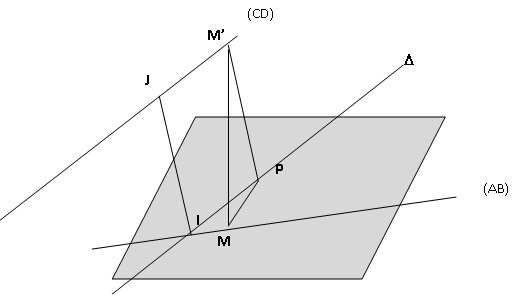a. Justifier que la parallèle à la droite (IJ) passant par M' coupe la droite D en un point P. Le point I n'appartenant pas à la droite (CD), ce point et cette droite définisent le plan (IJM'). La droite D étant parallèle à (CD) et passant par le point I, est donc incluse dans le plan (IJM'). Dans ce plan, la droite D est perpendiculaire à (IJ) et donc à la parallèle à (IJ) passant par M'. On conclut : la parallèle à la droite (IJ) passant par M' coupe la droite D en un point noté P. b. Démontrer que le triangle MPM' est rectangle en P. c. Justifier que MM' > IJ. Conclure. Dans le triangle rectangle MPM', l'hyporhénuse MM' est pluis grande que les côtés de l'angle droit. MM' > M'P ; or M'P = IJ ; donc MM' > IJ. IJ est la distance minimale entre les droites (AB) et (CD).

	Exercice 4 (5 pts). Un scooter radiocommandé se déplace en ligne droite à la vitesse constante de 1 m /s. Il est poursuivit par un chien qui se déplace à la même vitesse.. On représente la situation vue de dessus dans un repère orthonormé du plan d'unité 1 m. L'origine de ce repère est la position initiale du chien. Le scooter est représenté par un point appartenant à la droite d'équation x = 5. Il se déplace sur cette droite dans le sens des ordonnées croissantes. On étudie deux modélisations différentes de la trajectoire du chien. Partie A. Modélisation à l'aide d'une suite. 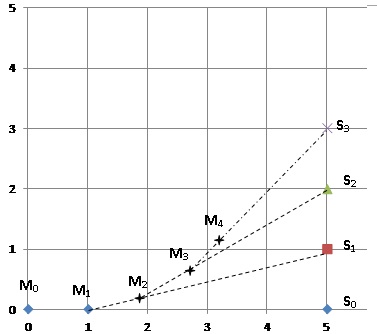A l'instant initial le scooter est représenté par le point S₀ et le chien par le point M₀. On considère qu'à chaque seconde le chien s'oriente instantanément en direction du scooter et se déplace en ligne droite sur une distance de 1 m. Ainsi à l'insatnt initial, le chien s'oriente en direction de S₀, et une seconde plus tard, il se retrouve en M₁. Le chien s'oriente en direction de S₁ et se déplace en ligne droite de 1 m et ainsi de suite. On modélise les trajectoires du chien et du scooter par deux suites de points notés (M_n) et (S_n). Au bout de n secondes, les coordonnées du point S_n sont ( 5 ; n). On note (x_n; y_n) les coordonnées du point M_n. 1. Construire sur le graphique les points M₂ et M₃. 2. On note d_n la distance entre le chien et le scooter n secondes après le début de la poursuite. d_n = M_nS_n. Calculer d₀ et d₁. d₀ =M₀S₀= 5 ; d₁ =M₁S₁= (1² +4²)^½ =17^½ . 3. Justifier que le point M₂ a pour coordonnées ( 1 + 4 / 17^½ ; 1 / 17^½). Equation de la droite S₁M₁ : y = a x +b. S₁(5 ; 1 ) appartient à cette droite :1 = 5a +b. M₁(1 ; 0 ) appartient à cette droite :0 = a +b soit b = -a. Par suite a = 0,25 et b = -0,25. y = 0,25 x -0,25. Les coordonnées de M₂ vérifient-elle cette équation ? 1 / 17^½ =0,25 +1 / 17^½ -0,25 ; cette égalité est vérifiée. Les coordonnées de M₂ vérifient l' équation de la droite (S₁M₁) : M₂ appartient à cette droite. Vérifions que M₁M₂ = 1 ; M₁M₂ ²=(1 + 4 / 17^½ -1)² +; 1 / 17 = 16 / 17 + 1 / 17 = 1. Le point M₂ a bien pour coordonnées ( 1 + 4 / 17^½ ; 1 / 17^½). 4. On admet que pour tout entier naturel n : x_n+1 = x_n +(5-x_n) / d_n ; y_n+1 = y_n +(n-y_n) / d_n ; a. le atableau ci-dessous, obtenu à l'aide d'un tableur donne les coordonnées des points M_n et S_n ainsi que la distance d_n en fonction de n. Quelles formules doit-on écrire dans les cellules C₅ et F₅ et recopier vers le bas pour remplir les colonnes C et F ? 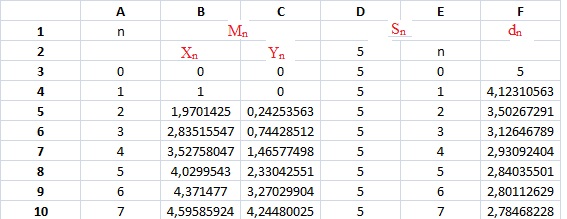En F5 : =RACINE((5-B5)^2+(E5-C5)^2)) En C5 : =C4+(A4-B4)/F4 b. On admet que la suite (d_n) est strictement décroissante. Justifier que cette suite est convergente et conjecturer de sa limite. Cette suite est strictement décroissante et minorée par la distance zéro ( une distance est positive ). Donc elle converge. D'après le tableau, sa limite est 2,77.
	Partie B. Modélisation à l'aide d'une fonction. On modélise la trajectoire du chien à l'aide de la courbe F de la fonction f définie pour tout réel x de [0 ; 5 [ par f(x) = -2,5 ln(1-0,2x)-0,5x +0,05x². 1. Lorsque le chien se trouve au point M de coordonnées (s ; f(x) de la courbe F, le scooter se trouve au point S, d'ordonnées y_S. La tangente à F en M passe par le point S. Cela traduit le fait que le chien s'oriente toujours en direction du scooter. On note d(x) la distance MS entre le chien et le scooter quand le chien est à l'abscisse x. a. Sur le graphe, construire sans calcul, le point S donnant la position du scooter lorsque le chien se trouve au point d'abscisse 3 et lire les coordonnées du point S. 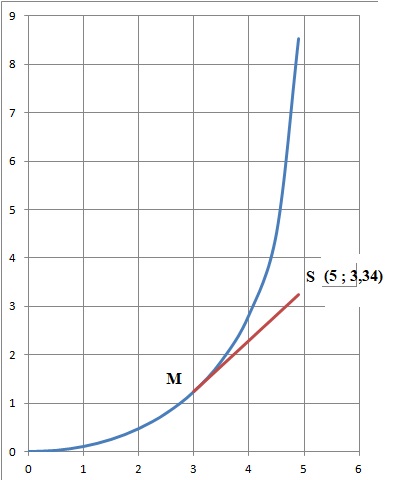b. On donne f ' la dérivée de la fonction f sur [0 ; 5[ et on admet que pour tout réel x de cet intervalle f '(x) = x(1-0,1x) / (5-x). Déterminer par le calcul une valeur approchée au centième de l'ordonnée du point S lorsque le chien est en M d'abscisse 3. Coefficient directeur de la tangente à la courbe en M : f '(3) = 3 0,7 / 2 = 1,05. Equation de cette tangente : y = 1,05 x +b. La tangente passe en M d'abscisse 3 et d'ordonnée f(3) = -2,5 ln(1-0,6)-1,5 +0,053²= 1,24. 1,24 = 1,05 x 3 +b ; b =-1,91. Equation de cette tangente : y = 1,24 x -1,91. Ordonnée du point S d'abscisse x = 5 : 1,05 x5 -1,91 =3,34. 2. On admet que d(x) = 0,1x² -x+5 pour tout réel x de [0;5[. Justifier qu'au cours du temps la distance MS se rapproche d'une valeur limite que l'on déterminera. Quand x tend vers 5, la limite de d(x) est : d(5) = 0,1 *5² -5+5 =2,5. Au cours du temps, MS tend vers 2,5 m.