Mathématiques,
probabilités, fonctions, Bac S Amérique du Nord 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Exercice
1. ( 6 pts).
Partie A.
Soit X une variable aléatoire qui suit la loi exponentielle de
paramètre 0,2.
1. On note g
la fonction définie sur l'intervalle [0 ; + oo[ par g(t) = 0,2t e-0,2t.
On définit la fonction G sur ce même intervalle par G(t) = (-t-5) e-0,2t.
Vérifier que G est une primitive de g.
On pose u = -t-5 et v = e-0,2t ; u' = -1 ; v' = -0,2e-0,2t.
u'v + v'u = - e-0,2t -0,2(-t-5)e-0,2t=0,2t) e-0,2t= g(t).
2.
En déduire que la valeur exacte de E(X) est 5.
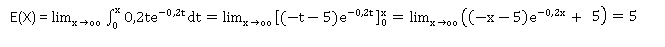
(-x-5) e-0,2x tend vers zéro quand x tend vers plus l'infini.
Partie B.
On modélise la durée, exprimée en minutes, passée dans le supermarché
par un client choisi au hasad par une variable aléatoire T.
Cette variable suit une loi normale d'eespérance 40 minutes et d'écart
type positif s.
On estime que P( T <10) = 0,067.
1. Déterminer la
valeur de l'écart type à la minute près.
On pose Y = (T-40) / s.
Y suit la loi normale centrée réduite.
P(T-40) < -30)=0,067 ; P(T-40) / s < -30 / s)=0,067 ; P(Y < -30 / s)=0,067 ;
La calculatrice conduit à : -30 / s = -1,476. s ~ 20.
2.
Dans cette question, on prend s
= 20 minutes. Quelle est la proportion de clients qui passent plus
d'une heure dans la supermarché ?
P(T > 60) = 1 -P(T < 60) = 1-0,841 =0,159. ( 15,9 %).
Partie C.
Les clients peuvent utiliser les bornes automatiques de paiement ou
bien les caisses gérées par un opérateur.
1.
La durée d'attente à une borne automatique, exprimée en minutes, est
modélisée par une variable aléatoire qui suit la loi
exponentielle de paramètre 0,2 min-1.
a. Donner la durée
moyenne d'attente d'un client à cette borne.
1 / 0,2 = 5 minutes.
b.
Calculer la probabilité que cette durée d'attente soit supérieure à 10
minutes.
exp(-0,2 x10) = e-2 ~0,135.
2. L'étude
commandée par le gérant conduit à la modélisation suivante :
- parmi les clients ayant choisi une borne automatique, 86 % attendent
moins de 10 minutes ;
- parmi les clients passant en caisse, 63 % attendent moins de 10
minutes.
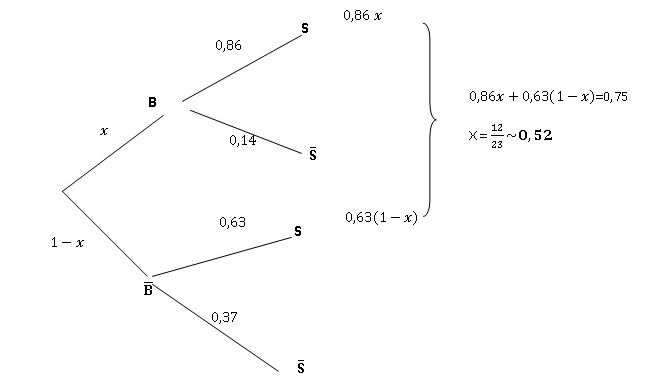
On choisit un client au hasard et on définit les événements suivants :
B : le client paye à la borne automatique.
non B : le client paye à une caisse avec opérateur.
S : la durée d'attente est de moins de 10 minutes.
Le gérant souhaite que 75 % des clients attendent moins de 10 minutes.
Quelle
est la proportion minimale de clients qui doivent choisir une borne
automatique de paiement pour que cet objectif soit atteint ?
Partie D.
Chaque client a droit à une carte à gratter par tranche de 10 €
d'achats. les cartes gagnantes représentent 0,5 % de l'ensemble du
stock de cartes. Ce stock est suffisamment grand pour assimiler la
distribution d'une acrte à un tirage avec remise.
1. Un client
effectue des achats pour un montant de 158,02 €
Quelle est la probabilité, arrondie à 0,01, qu'il obtiennent au
moins une carte gagnante ?
Le client possède 15 cartes.
On note X la variable aléatoire comptant le nombre de cartes gagnantes.
Les 15 tirages sont identiques, aléatoires, indépendants. Il y a
toujours deux issues possibles : G :" carte gagnante "ou carte non
gagnante.
p(G) = 0,005.
X suit la loi binomiale de paramètre n = 15, p = 0,005.
p(X >1 )= 1-p(X=0)
= 1-0,9275 ~0,07.
2.
A partir de quel montant d'achat, arrondi à 10 €, la probabilité
d'obtenir au moins une carte gagnante est-elle supérieure à 50 % ?
p(X >1 )= 1-p(X=0) =0,50.
p(X=0) = 0,5 = (1-0,005)n = 0,995n.
ln (0,5) = n ln(0,995) ; n = 138,3 soit 139 carte.
Minimum d'achat : 1390 €.
|
|
|
|
|
Exercice
2 (4 pts).
On lance un projectile dans un milieu fluide. L'objectif est de
déterminer pour quel angle de tir q
par rapport à l'horizontale la hauteur du projectile ne dépasse pas 1,6
m. On modèlise le projectile par un point qui se déplace, dans un plan
vertical, sur la courbe représentative de la fonction f définie sur
l'intervalle [0 ; 1 [ par :f(x) = bx +2 ln(1-x).
b est un paramètre réel supérieur ou égal à 2, x est l'abscisse du
projectile et f(x) son ordonnée.
1. On admet que f possède un maximum sur cet intervalle et que
f '(x) = (-bx+b-2) / (1-x)
Montrer que le maximum de la fonction f
est égal à b-2 +2 ln(2 / b).
La dérivée s'annule pour-bx+b-2=0 soit x = 1-2/b.
f(1-2 / b) = b-2+2 ln(2 / b).
2. Déterminer pour
quelles valeurs de b, la hauteur maximale atteinte ne dépasse pas 1,6 m.
Soit g(x) = x-2 +2 ln(2 /x) = x-2+2ln(x/2)
sur l'intervalle [2 ; +oo[.
g(x) ( somme de fonctions dérivables ) est dérivable sur cet intervalle.
g'(x) = 1-2 /x = (x-2) / x.
g(x) est continue, car dérivable, et strictement croissante sur cet
intervalle.
g(2) = 0, valeur inférieure à 1,6.
g(x) = x [1-2 / x -2 / x ln(x / 2)]
Quand x tend vers
l'infini :
2/x tend vers zéro ; on pose X = 2 /x : or X ln X tend vers zéro
; par suite g(x) tend vers plus l'infini.
D'après le corollaire du théorème des valeurs intermédiaires,
l'équation g(x) = 1,6 admet une unique solution, notée a, sur [2 ; +oo[.
Quand b appartient à [2 ; a],
la hauteur maximale ne dépasse pas 1,6 m.
3. On choisit b =
5,69.
3. Déterminer une
valeur approchée au dixième de degré près de l'angle q.
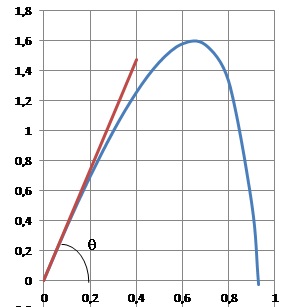
Coefficient directeur de la tangente à l'origine : f '(0) = b-2=3,69.
tang q = 3,69 ; q = 74,8 °.
|
|
|
|