Un instrument
à percussion, Bac S Amérique du Nord 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Les glockenspiels sont constitués de lames en acier de longueurs différentes et d'épaisseur identique.
Questions préliminaires.
1. Montrer que l'étude expérimentale du son produit par la 7ème lame de l'instrument est cohérente avec la note jouée.
Caractéristiques de la 7ème lame de l'intrument utilisé pour l'étude.
Note jouée : Si.
Dimensions ( longueur x largeur x épaisseur en mm : 101,0 x20,0 x2,0.
Gamme tonale Do4 La5.
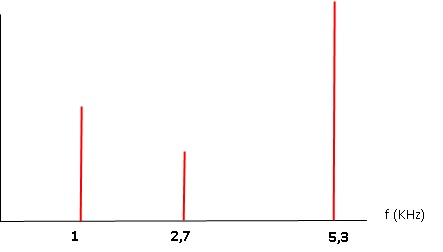
Spectre de Fourier du son produit par la 7ème lame de l'instrument ( note Si)
La fréquence du La3 est fixée par convention à 440 Hz.
Fréquence du La4 : 2 x440 = 880 Hz.
Dans la gamme tempérée, la division en 12 intervalles égaux implique que le rapport des fréquences du demi-ton est égal à 1,059.
Entre le La4 et le Si4, il y a deux demi-tons.
Fréquence du Si4 : 880 x1,0592 = 987 Hz.
Le spectre de Fourier montre que le pic de plus basse fréquence est 1000 Hz.
Les deux valeurs sont cohérentes.
2.
Discuter quantitativement la cohérence entre le modèle présenté et le
spectre de l'onde sonore obtenu expérimentalement avec la 7ème lame de l'instrument.
Le spectre de Fourier de l'onde sonore produite par ces lames est
composé de plusieurs pics dont les fréquences sont telles que :
fn = k e / L2 (2n+1)2.
k : constante liée au matériau de la lame ( m s-1).
e : épaisseur de la lame ( m).
L : longueur de la lame (m).
n : nombre entier positif. n = 1 correspond au fondamental.
f2 / f1 = (5 / 3)2 = 2,78.
f2 = 1 x2,78 = 2,78 kHz.
f3 / f1 = (7 / 3)2 = 5,44.
f3 = 1 x5,44 = 5,44 kHz.
Il y a cohérence entre le modèle présenté et le spectre de l'onde.
|
|
|
|
|
Problème.
Prévoir les longueurs des lames à chaque extrémité de l'instrument.
Evaluer la cohérence de ces résultats à l'aide de la photographie. Commenter.
Gamme tonale Do4 La5.
Entre le Do4 et le La4, il y a 9 demi-tons.
Fréquence du La4 / fréquence du Do4 = 1,0599=1,675.
Fréquence du Do4 =880 / 1,675 ~525 Hz.
f1 = k e / L2 (3)2.
On détermine k à partir de la fréquence du Si4 :
k = f1 L2 /(9e) =987 x0,1012 /(9x2 10-3)~559 m s-1.
Longueur de la lame du Do4 : (9ke / f1)½ = (9 x559 x 0,002/ 525)½ =0,138 ~0,14 m.
Sur la photographie, la lame la plus longue mesure 8,2 cm.
Echelle : 20,2 cm sur la photo correspond à 34 cm réels.
Longueur de cette lame : 8,2 x34 / 20,2 =13,8 cm.
Donc résultats cohérents.
Fréquence du La5 f1 =: 2 x880 = 1760 Hz.
Longueur de la lame du La5 : (9ke / f1)½ = (9 x559 x 0,002/ 1760)½ =0,0756 ~0,076 m.
Sur la photographie, la lame la plus petite mesure 4,5 cm.
Echelle : 20,2 cm sur la photo correspond à 34 cm réels.
Longueur de cette lame : 4,5 x34 / 20,2 =7,6 cm.
Donc résultats cohérents.
Il est difficile de construire des glockenspiels pouvant jouer des notes plus élevées que le La5,( longueur de cette lame : seulement 7,5 cm).
|
|
|
|