Physique
chimie, robot de tonte,
Bac Sti2d, stl, Polynésie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Pour l'entretien de la pelouse de
son jardin, monsieur Green vient de faire l'acquisition d'un robot
tondeuse autonome.
Le sujet propose l’étude, en trois parties
indépendantes, de cette machine et de son environnement.
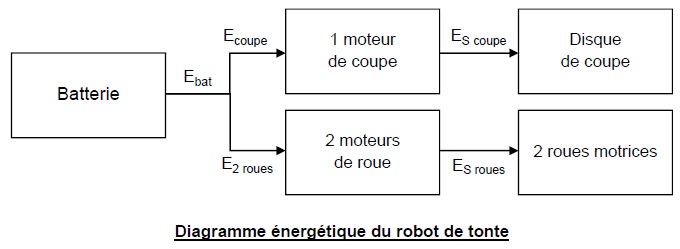
PARTIE A – ÉTUDE MÉCANIQUE DU ROBOT TONDEUSE
A.1 Étude du robot
tondeuse sur terrain plat
A.1.1 Étude
énergétique
Le but de cette partie est de vérifier que le robot tondeuse aura assez
d’énergie pour rentrer à sa station de recharge après une heure de
tonte.
Sur un terrain plat avec une certaine densité de pelouse, on considère
que :
la puissance moyenne demandée par le moteur de coupe est Pcoupe
= 30,0 W,
la puissance moyenne demandée par le moteur d’une roue est P1roue
= 6,50 W,
la vitesse moyenne de déplacement du robot tondeuse est v = 0,42 m.s-1,
la durée moyenne de tonte est Δttonte = 60 min.
A.1.1.a Rechercher,
dans le tableau des caractéristiques techniques, la tension, Ubat,
délivrée par la batterie, la charge totale, Qbat, et
l’énergie stockée
dans la batterie, Ebat.
Ion – Lithium Ubat = 18 V ; Qbat =
3,2 A.h ; Ebat= 57,6 W.h
A.1.1.b À l’aide
d’une analyse dimensionnelle, vérifier par un calcul la cohérence de la
valeur de Ebat avec celles de Ubat et de Qbat.
Ebat
(Wh )= Qbat
(Ah)x Ubat
(V) = 3,2 x 18 = 57,6 Wh.
Pour une
durée de tonte de Δttonte = 60 minutes :
A.1.1.c Donner
l’expression littérale de l’énergie, Ecoupe, demandée par le
moteur allié au disque de coupe en fonction de la puissance, Pcoupe,
et de la durée de tonte Δttonte. Calculer Ecoupe
(en W.h).
Ecoupe,
= Pcoupe,
x Δttonte.
=30,0 x1 = 30,0 W h.
A.1.1.d Calculer l’énergie, E2
roues (en W.h), demandée par l’ensemble des 2 moteurs de roue.
E2
roues = 2 P1roue x Δttonte.
= 2 x 6,5 x1 = 13 W h.
A.1.1.e En déduire que l’énergie
restant dans la batterie pour retrouver la station de charge vaut Erestant
= 14,6 W.h au bout 60 minutes de tonte.
Erestant
=Ebat
(Wh ) - Ecoupe,
- E2
roues =57,6 -30 -13 = 14,6 Wh.
A.1.1.f Lorsque le robot rentre à sa
station de charge, seuls les moteurs des roues sont en fonctionnement.
Connaissant l’énergie restant dans la batterie, quelle pourrait être la
durée maximale de la phase de retour du robot à sa station de charge ?
Commenter.
Durée =Erestant
/ ( 2 P1roue
) = 14,6 /
13 ~1,12 h ~1 h 7 min.
Il a suffisamment d'énergie pour rentrer à la station de charge.
A.1.2 Étude des intensités demandées
à la batterie
Le but de cette partie est d’estimer l’intensité débitée par la
batterie afin de dimensionner et de choisir ultérieurement cette
batterie.
A.1.2.a Les 3
moteurs nécessitent une tension de 18,0 V.
Compléter le schéma électrique en y ajoutant les deux moteurs de
roue. Préciser sur le schéma le sens du courant dans les moteurs des
roues, Iroue, ainsi que la tension, U, aux bornes des
différents moteurs.
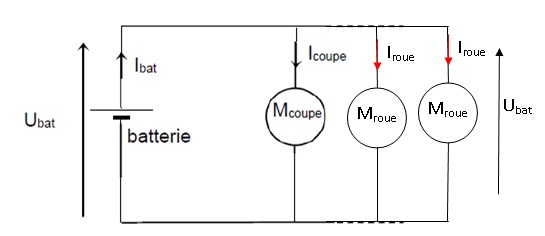
A.1.2.b Donner
l’expression littérale du courant, Icoupe, demandé par le
moteur de coupe en fonction de Pcoupe et Ubat.
Calculer Icoupe.
Icoupe = Pcoupe
/ Ubat = 30,0 /
18,0 = 1,67 A.
A.1.2.c Parmi les
intensités suivantes, quelle est celle qui correspond à l’intensité, I2
roues, demandée par l’ensemble des 2 roues motrices ?
0,72 A ; 0,36 ;
1,38 ; 2,77 A.
I2
roues = P2
roues / Ubat = 13,0 /
18,0 = 0,72 A .
A.1.2.d Calculer l’intensité du
courant fourni par la batterie lorsque le robot tond.
1,67 +0,72 ~2,39 A.
|
|
|
|
|
A.1.3
Étude des forces en action sur le robot
A.1.3.a Le
rendement des moteurs des roues vaut η = 90 %. Calculer la puissance de
sortie, PS 2 roues, sur l’ensemble des 2 roues.
PS 2
roues, = 0,9 x13,0 = 11,7 W.
Le robot
tondeuse se déplace linéairement sur un terrain horizontal à la vitesse
constante v = 0,42 m.s-1.
On donne, pour un mouvement rectiligne :
P = F × v avec P : puissance en watts (W), F : force en newtons (N), v
: vitesse en m.s-1.
A.1.3.b Montrer que
la force d’entraînement du robot tondeuse, Ftondeuse, vaut
environ 28 N.
Ftondeuse,
= PS 2
roues, / v = 11,7 / 0,42 = 27,85 ~28 N.
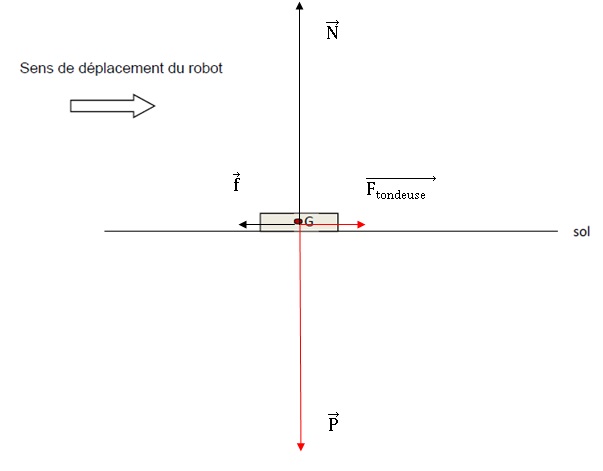
A.1.3.c Représenter
au centre de gravité, G, les forces ci-dessous avec l’échelle 1 cm pour
20 N. Expliquer votre raisonnement et détailler vos calculs.
le poids, verticale vers le bas, valeur P = m g = 11,8 x9,81 ~
116 N.
la réaction normale au sol, N, verticale, vers le haut, valeur 116 N.,
la force d’entraînement du robot tondeuse, Ftondeuse,
les forces de frottements résistants, f opposées à Ftondeuse, le
mouvement étant rectiligne uniforme.
A.2 Étude du robot
tondeuse sur terrain incliné
Une partie du terrain de monsieur Green possède une pente de a
= 20°. Monsieur Green se demande si la batterie du robot tondeuse est
suffisante pour que le robot tonde pendant une heure sur son terrain en
pente.
La force résultante des frottements résistants, f , entre le robot et
la pelouse sont considérées constantes et égales à 28 N.
On considère également que la vitesse de déplacement rectiligne du
robot tondeuse reste constante et vaut 0,42 m.s-1.
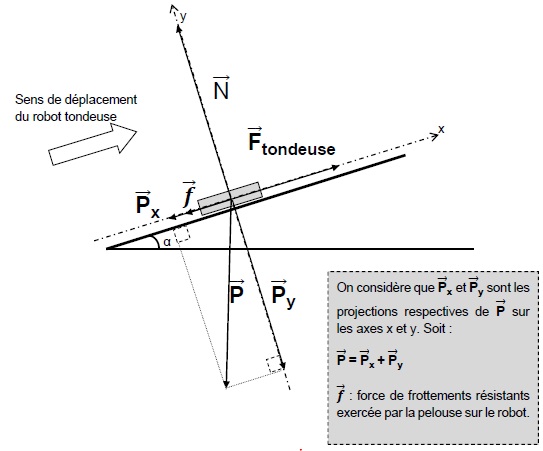
A.2.1 En vous
aidant du graphique ci-dessus (1,0 cm représente 20 N), mesurer la
composante du poids, Px.
2 cm soit Px = 40 N.
A.2.2 Donner la
relation entre Ftondeuse, f et Px. Expliquer.
Le mouvement étant rectiligne uniforme, la somme vectorielle des forces
appliquées au robot est nulle.
Px + f = Ftondeuse.
A.2.3 En déduire la
valeur de la force d’entraînement Ftondeuse.
Ftondeuse
= 40 +28 =
68 N.
A.2.4 Une énergie
de 61,4 W.h est nécessaire pour que le robot tonde pendant une heure
sur un terrain en pente de 20°, puis retourne à sa station de charge.
La batterie étant initialement chargée à son maximum, le robot peut-il
effectuer cette tâche ?
Ebat=
57,6 W.h, valeur inférieure à 61,4 Wh. Le robot ne peut pas accomplir
cette tache.
|
|
PARTIE B – AUTONOMIE
DU ROBOT TONDEUSE
B.1 Étude de la batterie
B.1.1 Étude
chimique de la batterie
On donne le schéma de l’accumulateur Li-Ion en charge :

B.1.1.a Quels sont
les porteurs de charge responsables du passage du courant dans
l’électrolyte ?
Les ions lithium Li+.
B.1.1.b Quels sont
les porteurs de charge responsables du passage du courant dans les fils
du circuit électrique ?
Les électrons.
B.1.1.c Représenter
le sens de déplacement de tous les porteurs de charge lors de la
décharge de la batterie .
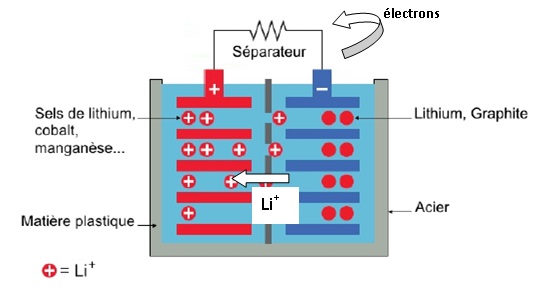
B.1.1.d Recopier
sur votre copie et compléter les demi-équations électroniques lors de
la décharge de la batterie :
à l’électrode du pôle - :C + Li =C +.Li++e-
.
à
l’électrode du pôle + : CoO2 + Li+ +e- = CoLiO2
B.1.1.e Comment
s’appelle la réaction qui a lieu sur l’électrode du pôle - lors de la
décharge ?
L'oxydation du réducteur Li libère des électrons.
B.1.2 Étude des
caractéristiques techniques de la batterie
Sur les anciens modèles de robots tondeuses, les batteries avaient les
caractéristiques suivantes : Ni-MH / 18,0 V / 2,20 A.h.
Monsieur Green se renseigne sur les caractéristiques des deux types de
batteries en se demandant s’il pourrait remplacer sa batterie
Lithium-Ion par une ancienne batterie Ni-MH qui coûte moins cher.
B.1.2.a L’énergie
de la batterie Li-Ion vaut 57,6 W.h lorsqu’elle est complètement
chargée. Donner un encadrement de la masse de la batterie Li-Ion.
De 90 à 110 Wh par kilogramme.
57,6 /9 0 = 0,64 kg ; 57,6 / 110 =0,52 kg.
B.1.2.b L’énergie
nécessaire au robot dépend de sa masse, donc de celle de sa batterie.
Expliquer, sans calcul, un des intérêts d’une batterie Li-Ion par
rapport à une batterie Ni-MH.
La densité énergétique de la batterie Ni-MH est comprise entre 55 et 65
Wh kg-1. Sa masse serait de l'ordre de 1 kg, bien supérieure
à la masse de la batterie Li-ion.
B.1.2.c Donner deux
autres raisons pour lesquelles les batteries Ni-MH ont été remplacées
par des batteries Li-Ion.
La batterie Li-ion peut être rechargée plus de 1000 fois. Sa densité
d'énergie volumique est plus élevée.
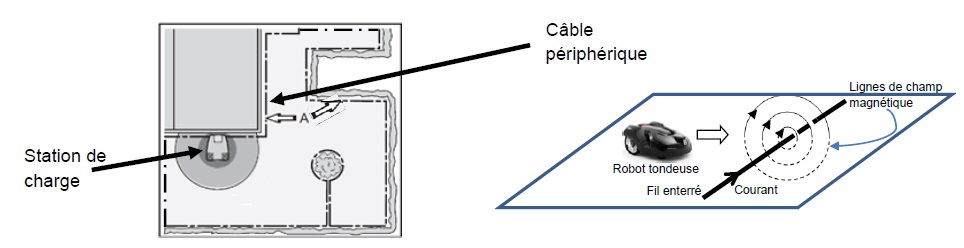
B.2 Délimitation de la zone de tonte
Le robot tond de façon aléatoire jusqu’au moment où il se rapproche du
câble périphérique. Il capte alors le champ magnétique émis par le
câble (signal A) et rebrousse chemin.
Plan de la zone de tonte, délimitée par un câble périphérique :
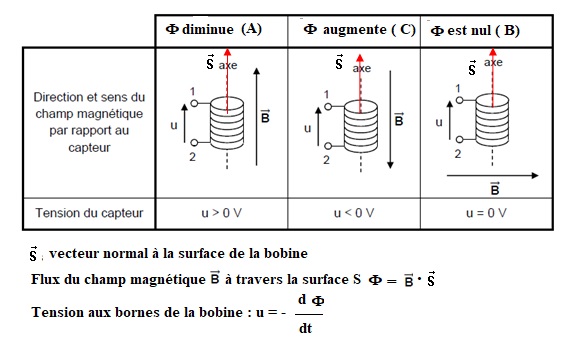
Le capteur utilisé pour détecter le champ magnétique, B, est un capteur inductif (une bobine) qui sera modélisé par le symbole.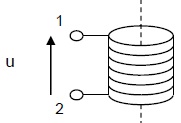
B.2.1 Étude des signaux émis par la station de charge
Monsieur Green souhaiterait installer seul le robot tondeuse, sa
station de charge et le câble périphérique. Le technicien lui indique
le principe de fonctionnement du capteur de champ magnétique.
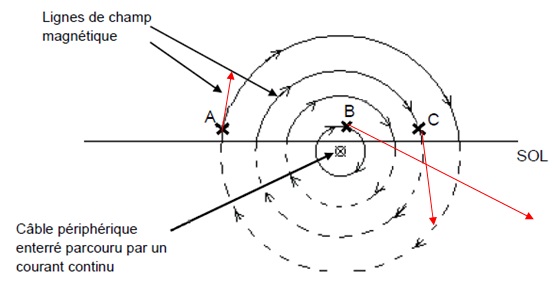
B.2.1.a Lustifier l’existence d’un champ magnétique, B à proximité du câble périphérique.
Un conducteur parcouru par un courant électrique se comporte comme un aimant.
B.2.1.bTracer les
vecteurs champ magnétique aux points A, B et C, sachant que les
intensités des champs magnétiques aux différents points sont :
B(A) = 10,0 mT, B(B) = 50,0 mT, B(C) = 20,0 mT.
On prendra comme échelle : 1,0 cm pour 10,0 mT.
B.2.1.c Que signifie le T dans mT ?
Tesla.
B.2.2 Capture des signaux émis par la station de charge.
B.2.2.a Justifier clairement que la tension, u, du capteur est positive en A, nulle en B, négative en C.
B.2.2.b Monsieur
Green souhaiterait poser seul le câble périphérique. Le technicien
indique une erreur à éviter. Expliquer pourquoi la pose du
câble suivant le schéma a) risque d’immobiliser le robot à proximité du massif des plantes à éviter.
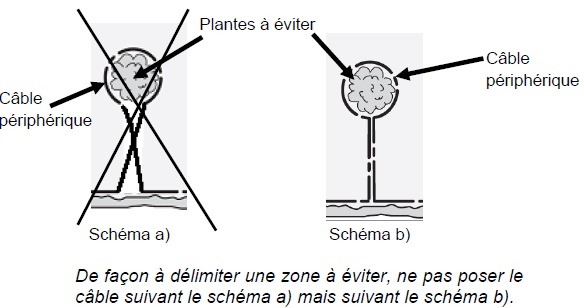
Schéma a) : Au croisement les deux câbles électriques sont parcourus
par des courants de sens contraire. Il en résulte deux champs
magnétiques difficilement interprétables par le robot.
PARTIE C – ENTRETIEN DE LA PELOUSE
C.1 Traitement contre la mousse.
Monsieur Green décide donc de mettre du carbonate de calcium de formule CaCO3(s) sur sa pelouse afin de diminuer l’acidité de son terrain.
C.1.1 Le pH d’une solution aqueuse est lié à la concentration d’un ion spécifique. De quel ion s’agit-il ?
Ion oxonium H3O+.
Le carbonate de calcium est un solide ionique formé par les ions calcium Ca2+ et les ions carbonates CO32-. Les ions CO32- font partie du couple acide-base HCO3- / CO32-.
C.1.2 Les ions carbonates CO32- correspondent-ils à la forme acide ou à la forme basique de ce couple ?
Les ions CO32- correspondent à la forme basique de ce couple. Ils sont capable de gagner un prpton H+.
C.1.3 Recopier, compléter et équilibrer la demi-équation chimique suivante :
H+ + CO32- = HCO3- .
C.1.4 Les ions carbonate HCO3- réagissent avec les ions H3O+. L’eau fait partie du couple acide-base H3O+ / H2O.
Écrire la demi-équation chimique du couple H3O+ / H2O.
H3O+ = H2O +H+.
C.1.5 Montrer que le bilan de la réaction du carbonate de calcium avec les ions oxonium peut s’écrire :
CO32-+ H3O+ = HCO3- + H2O (1)
La base la plus forte CO32-réagit spontanément avec l'acide le plus fort H3O+.
H+ + CO32- = HCO3- .
H3O+ = H2O +H+.
Ajouter et simplifier : CO32-+ H3O+ = HCO3- +H2O.
De plus, les ions hydrogénocarbonate HCO3- réagissent avec les ions oxonium H3O+selon l’équation chimique suivante :
HCO3- + H3O+ = H2O + CO2,H2O (2).
C.1.6 À partir des équations ci-dessus, justifier que le carbonate de calcium diminue l’acidité du sol.
Les réactions (1) et (2) consomment des oins H3O+ . La concentration des ions H3O+ dans le sol diminue. L'acidité du sol décroït.
C.2 Récupération de l’eau de pluie
Afin d’arroser son gazon, monsieur GREEN décide d’utiliser l’eau de
pluie récupérée dans une cuve enterrée suivant le schéma ci-dessous. Il
se demande quelle est la puissance minimale à choisir pour la pompe.
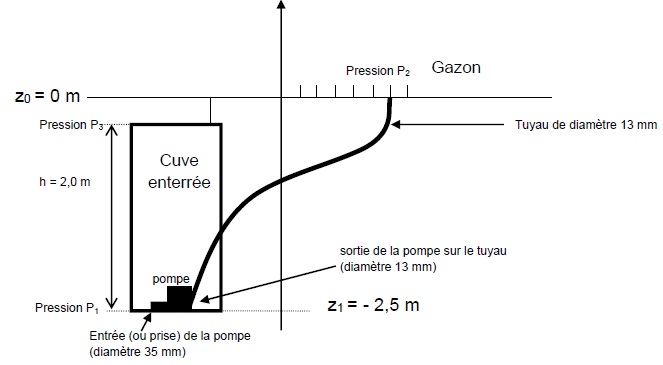
À l’aide d’un tuyau de diamètre 13 mm, monsieur Green aimerait assurer un débit de 50 L.min-1 pour l’arrosage de son jardin. La cuve est de forme cylindrique, de rayon 60 cm et de hauteur 2,0 m.
C.2.1 Convertir le débit volumique Dv = 50 L.min-1 en m3.s-1.
50 10-3 / 60 = 8,3 10-4 m3 s-1.
C.2.2 La surface de la section du tuyau vaut S = 1,33 × 10-4 m2. En déduire que la vitesse, v2, de sortie de l’eau est, dans ce cas, d’environ de 6,3 m.s-1.
v2 = Dv / S = 8,3 10-4 / (1,33 × 10-4 )~6,3 m.s-1.
C.2.3 Exprimer la pression, P1, à l’entrée de la pompe (ou prise) en fonction de la pression, P3, en haut de la cuve et de la hauteur d’eau, h. Préciser les unités.
P1 = P3 +rgh.
r : masse volumique de l'eau en kg m-3 ; g = 9,81 m s-2 et h (mètre).
C.2.4 On considère que la cuve est pleine. On donne la pression au niveau de la surface de l’eau dans la cuve : P3 = 1,00 bar. Démontrer que P1 vaut 1,20 bar.
P1 = 1,00 105 + 1000 x9,81 x2,0 = 1,2 105 Pa = 1,2 bar.
C.2.5 Dans une revue scientifique, on trouve la relation de dimensionnement de la pompe :
Pu / Dv =½r (v22-v12) + r g ( z2-z1) +P2-P1.
La vitesse de l’eau en entrée de la pompe est de 0,87 m.s-1. P2 = 1,0 bar. z2 = 0 m.
Vérifier qu’une pompe de puissance utile 20 W serait dimensionnée pour remonter l’eau de la cuve.
Pu / Dv =500(6,32-0,872) +1000 x9,81 x2,5 -2 104 = 1,95 104 +2,45 104 -2 104 = 2,4 104 Pa.
Pu = 2,4 104 x 8,3 10-4 ~ 20 W.
|
|