Physique chimie, la station spatiale internationale ISS, Bac Sti2d, stl biotechnologie Métropole 2018

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

PARTIE A : Production d’énergie électrique à bord de l’ISS.
La production d’électricité à bord de l’ISS est assurée par l’utilisation de 8 panneaux solaires doubles appelés SAW (Solar Array Wing). L’orientation par rapport au Soleil de ces panneaux est contrôlée en permanence de façon à optimiser la production d’énergie électrique.
A.1. Autour du rendement d’un SAW
Chaque SAW comporte plusieurs milliers de cellules photovoltaïques et a un rendement moyen théorique h de conversion d’énergie lumineuse en énergie électrique de 14,5 %.
A.1.1. Compléter la chaîne énergétique d’une cellule photovoltaïque.

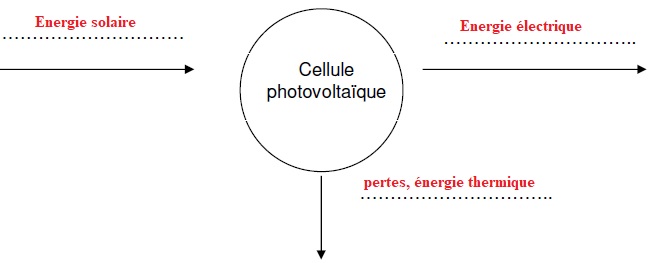
A.1.2.1. Montrer que la surface totale S d’un SAW vaut environ 389 m².
Dimensions d'un SAV : 33,5 x11,6 m ; S = 33,5 x11,6 =388,6 ~389 m².
A.1.2.2. Déterminer la puissance lumineuse théorique maximale P_lmax reçue par un panneau SAW.
Eclairement incident : 1 500 W · m^-2 ; P_lmax = 1500 x 388,6=5,829 10⁵ ~5,8 10⁵ W.
A.1.2.3. En déduire la puissance électrique théorique maximale P_emax que pourrait générer un panneau SAW.
P_emax = 5,829 10⁵x 0,145 =8,45 10⁴ W~84 kW.
A.1.2.4. En réalité, la puissance électrique attendue pour chaque panneau par les ingénieurs est d’environ 31 kW. Déterminer la puissance électrique P_e attendue par les ingénieurs par les 8 SAW.
P_e = 8 x31 = 248 kW.
A.1.2.5. Déterminer la puissance électrique effective totale P_tot générée par l’ensemble des 8 panneaux SAW le 5 novembre 2017 à 21h45.

Identification du SAW	1B	3B	3A	1A	2A	4A	4B	2B	Total
Puissance électrique fournie (W)	8693	6502	6484	4828	8409	8967	8466	7506	5,98 10⁴

A.1.2.6. Montrer que les panneaux du SAW ne sont utilisés qu’à environ 24% de leur possibilité le 5 novembre 2017 à 21h45.
59,8 / 248~0,24 ( 24 %).
A.1.2.7. Proposer une explication.
A cette heure, ce jour là, l'éclairement incident est inférieur à 1500 W m^-2.
A.1.2.8. Au cours de chacune de ses orbites autour de la Terre qu’elle effectue en 90 minutes, la station orbitale passe 36 minutes dans l’ombre de la Terre. Comment selon vous la station orbitale fait-elle pour subvenir à ses besoins en énergie électrique durant ces 36 minutes ?
L'excédent d'énergie électrique fournie par les panneaux est utilisée pour charger des accumulateurs. Ces derniers alimentent la station quand elle passe dans l'ombre de la terre.
A.2. Du vent dans les panneaux ?
A.2.1. Dans le référentiel géocentrique la station orbitale décrit un mouvement considéré comme circulaire de rayon R_station= 6 770 km. Calculer en km/h la vitesse v de la station orbitale.
La station parcourt la circonférence 2 p R_station en 90 x60 =5400 s.
v = 2 x3,14 x 6,77 10⁶ / 5400 = 7,877 10³ m /s soit 7,877 10³ x3,6 ~ 2,8 10⁴ km /h.
A.2.2. Vu le résultat de la question précédente, justifier le fait que les panneaux ne soient pas arrachés.
A cette altitude, il n'y a pratiquement plus d'air, donc plus de frottement.

PARTIE B : Production de dioxygène au sein de l’ISS
Afin de couvrir les besoins en dioxygène des six membres d’équipage de l’ISS, un nouveau système a été installé en 2007 dans la station : l’OGS (Oxygen Generator System). Le principe de l’OGS repose sur l’électrolyse de l’eau en milieu basique.
B.1. Mise en équation.
La production du dioxygène est assurée par une réaction d’oxydo-réduction en milieu basique.
À l’une des électrodes, la demi-équation (1) s’écrit :
2 H₂O(l) + 2 e^-= H₂ (g) + 2 HO^- (aq) (1)
À l'autre électrode, la demi-équation (2) s'écrit :
4 HO^- (aq) = 2 H₂O(l) + 4 e^- + O₂ (g) (2)
B.1.1. Nommer le couple d’oxydo-réduction relatif à la demi-équation (1).
H₂O(l) / H₂ (g).
B.1.2. L’électrode où se forme le dihydrogène H₂ est-elle l’anode ou la cathode ? Justifier.
H₂O est réduite en dihydrogène à la cathode négative.
B.1.3. À partir des demi-équations (1) et (2), établir l’équation globale de fonctionnement de l’électrolyseur.
4 H₂O(l) + 4 e^-= 2H₂ (g) + 4 HO^- (aq).
4 HO^- (aq) = 2 H₂O(l) + 4 e^- + O₂ (g)
Ajouter et simplifier : 2 H₂O(l) = 2H₂ (g) + O₂ (g).
B.1.4. Le dihydrogène formé se combine avec du dioxyde de carbone. Ecrire l’équation de la réaction se produisant dans le réacteur de Sabatier.
Le dihydrogène est acheminé vers un réacteur appelé réacteur de Sabatier où il se combine avec du dioxyde de carbone CO₂ pour former de l’eau et
du méthane CH₄.
4H₂(g) + CO₂(g) =2 H₂O(l) + CH₄(g).
B.1.5. Donner deux intérêts qui selon vous justifient l’usage du réacteur de Sabatier.
Valorisation du dihydrogène sous forme de méthane, combustible.
Elimination du dioxyde de carbone produit par la respiration des occupants de la station.
Production d'eau utile pour les astronautes.
B.2. Étude quantitative.
Données :
· température q à l’intérieur de l’ISS : q = 25 ° C ; · pression P à l’intérieur de l’ISS : P = 1,0 bar = 1,0 × 10⁵ Pa ;
· quantité d’électricité Q disponible exprimée en Coulomb (C) : Q = n_e- · F = I · Dt
ne- : quantité maximale d’électrons circulant exprimée en moles (mol)
F : constante de Faraday ; F = 9,65 × 10⁴ C · mol ^-1;
B.2.1. Calculer la quantité d’électricité Q nécessaire au fonctionnement d’une cellule de l’OGS au cours d’une journée.
I = 50 A ; Dt = 24 x3600 = 8,64 10⁴ s.
Q = 50 x8,64 10⁴ = 4,32 10⁶ ~4,3 10⁶ C.
B.2.2. En déduire la quantité d’électrons n_e- (exprimée en mol) échangée au cours d’une journée par une cellule électrolytique.
n_e- = Q / F = 4,32 10⁶ / (9,65 × 10⁴ ) =44,76 ~45 mol.
B.2.3. À l’aide de la demi-équation :
4 HO^- (aq) = 2 H₂O(l) + 4 e^- + O₂ (g) (2)
Vérifier que la quantité de matière de dioxygène produite n(O₂ ) par une cellule électrolytique pendant une journée est environ 11 mol.
n(O₂ )= n_e- / 4 = 44,76 / 4 = 11,19 ~11 mol.
B.2.4. L’équipage de l’ISS consomme 0,91 kg de dioxygène par personne et par jour.
Déterminer le nombre minimal de cellules électrolytiques nécessaires pour subvenir aux besoins en dioxygène de l’équipage.
Quantité de matière de dioxygène consommée par personne et par jour : 0,91 x1000 / 32 ~28,4 mol.
Soit pour 6 personnes : 6 x28,4 ~171 mol.
Nombre de cellules : 171 / 11 ~15,5 ( 16 cellules).
B.2.5. À la température q de 25 °C et sous une pression P de 1,0 bar, le dioxygène se trouve à l’état gazeux.
B.2.5.1. Connaissant la pression P d’un gaz et sa quantité de matière n à une température absolue T donnée, il est possible de calculer le volume V occupé par ce gaz grâce à la loi des gaz parfaits : P · V = n · R · T
avec : P : pression du gaz exprimée en Pa
V : volume occupé par le gaz en m³
n : quantité de matière du gaz en mol
R : constante des gaz parfaits ; R = 8,31 J · K^-1 · mol^-1
T : température absolue du gaz en K
Calculer à la température de 25 °C, le volume de dioxygène V(O₂ ) produit par une cellule de l’OGS en un jour.
V = nRT / P = 11,19 x8,31 x 298 / 10⁵ = 0,277 ~0,28 m³.
B.2.5.2. Calculer le volume de dioxygène V(O₂ ) _mission produit par une cellule de l’OGS au cours de la mission de Thomas Pesquet ( 196 jours ).
0,277 x 196 =54,3 ~54 m³.

PARTIE C : Sorties de l’ISS
Plus gros objet artificiel en orbite terrestre, l’ISS a été construite progressivement au cours de nombreuses sorties extravéhiculaires des différents astronautes. Pour survivre et travailler dans l’espace, un astronaute doit revêtir une combinaison spatiale très spécifique :
l’EMU (Extravehicular Mobility Unit).
C.1. Élimination du dioxyde de carbone lors des sorties extravéhiculaires
La dernière version des EMU offre une autonomie de 9 h en dioxygène. Elle est équipée d’un système de survie très perfectionné dont une partie a pour but d’évacuer le dioxyde de carbone expiré par l’astronaute.
C.1.1. Le dioxyde de carbone et la vapeur d’eau expirés par l’astronaute, proviennent de la combustion du glucose dans le dioxygène. Ecrire et équilibrer l’équation de combustion complète du glucose de formule chimique C₆H₁₂O₆.
C₆H₁₂O₆+ 6O₂ = 6CO₂ + 6H₂O.
C.1.2. Dans l’EMU, le dioxyde de carbone, gaz à caractère acide, est acheminé vers des cartouches d’hydroxyde de lithium où il réagit afin de former du carbonate de lithium et de l’eau.
C.1.2.1. Donner la signification du pictogramme associé à l’hydroxyde de lithium.

C.1.2.2. Donner la conduite à tenir en cas de contact accidentel avec l’hydroxyde de lithium dans un laboratoire.
Laver abondamment avec de l'eau.
C.2. Retour sur Terre
Les astronautes passent en moyenne 6 mois à bord de l’ISS. Ainsi, le 2 juin 2017 à 16h09, Thomas Pesquet a touché à nouveau le sol terrestre après un vol de retour de près de 4 heures à bord du vaisseau Soyouz MS-03.
C.2.1. Montrer que l’énergie cinétique E_c du module de descente varie de - 44 kJ entre les points A et B.
À 70 cm du sol, c'est au tour des six rétrofusées de s'allumer pour réduire au maximum la vitesse du module de descente qui passe alors de 22 à 5,0 km · h^-1 (vitesse lors de l’impact au sol). Masse du module m = 2500 kg.
Vitesse initiale 22 km / h soit 22 / 3,6 ~6,1 m /s.
Energie cinétique initiale : ½mv² = 0,5 x2500 x6,1² = 4,668 10⁴ J =46,68 kJ
Vitesse finale 5,0 km / h soit 5,0 / 3,6 ~1,38 m /s.
Energie cinétique finale : ½mv² = 0,5 x2500 x1,38² = 2,41 10³ J= 2,41 kJ.
Varition de l'énergie cinétique : 2,41 -46,68 = -44,27 ~ - 44 kJ.
C.2.2. Exprimer puis calculer le travail W_AB du poids.
W_AB = mg AB = 2500 x9,81 x 0,70 ~ 1,7 10⁴ J ~17 kJ.
C.2.3. Ce travail est-il moteur ou résistant ? Justifier.
Le travail du poids est moteur en descente.
C.2.4. Déterminer le travail W de la force de frottement entre les points A et B.
La somme des travaux des forces est égale à la variation de l'énergie cinétique.
W + 17 = - 44 ; W = -61 kJ.
C.2.5. En supposant la force de freinage f constante entre A et B, déduire l’intensité f de cette force de freinage.
W = - f AB ; f = 61 /0,7 ~ 87 kN.