Formation
d'une cavité souterraine, Bac S métropole 09/2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Cette
cavité, que l’on suppose cylindrique, a un diamètre d’ouverture de 35 m
et une profondeur de 103 m, et permet d’atteindre une galerie
souterraine où il règne une température proche de 13 °C.
L’objectif de cet exercice est d’estimer la durée nécessaire à la
formation de cette cavité souterraine. On émet l’hypothèse que cette
dernière s’est formée par disparition du carbonate de calcium CaCO3 (calcite) présent dans les roches calcaires par réaction avec l’eau de pluie s’infiltrant dans le sol.
Données :
masses molaires atomiques : M(C) = 12,0 g.mol-1, M(O) = 16,0 g.mol-1, M(Ca) = 40,1 g.mol-1 ;
masse volumique moyenne de la calcite ou carbonate de calcium CaCO3 (s) : ρ = 2,7 × 103 kg.m-3 ;
1 mm de précipitations équivaut à 1 L d’eau de pluie par m² au sol.
L’eau de pluie
L’eau de pluie, par contact avec l’air et lors de son passage dans la végétation, se charge en dioxyde de carbone CO2.
Le dioxyde de carbone étant une espèce acide, sa dissolution dans l’eau
de pluie s’accompagne d’une acidification de cette eau.
Solubilité de la calcite dans l’eau de pluie en fonction du pH.
La solubilité d’une espèce chimique dans un solvant correspond à la
quantité de matière maximale de cette espèce que l’on peut dissoudre
par litre de solution. On considère que la valeur du pH de l’eau de
pluie infiltrée dans le sol aux alentours de Padirac est comprise entre
4,5 et 6. La solubilité de la calcite correspond à la quantité de
matière maximale de calcite « dissoute » par litre d’eau de pluie après
réaction.
pH
|
4,5
|
5,0 |
5,5
|
6,0
|
solubilité de la calcite ( mmol / L)
|
3
|
1
|
0,6
|
0,2
|
|
|
|
|
|
Questions préliminaires
1. On admet qu’environ 70 % des
précipitations (pluie, neige,…) s’infiltrent dans la roche aux environs
de Padirac. Vérifier que le volume d’eau de pluie qui s’infiltre à
travers une surface correspondant à celle de l’ouverture du gouffre
durant l’année 2015 est de l’ordre de 6 × 105 L.
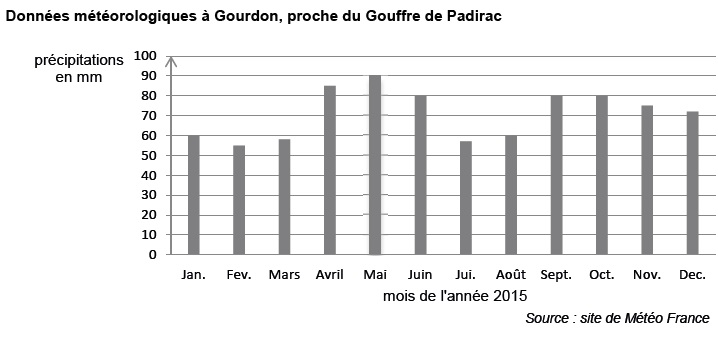
Volume des précipitations en 2015 :
60 +54 +59 +83 +90 +80 +57 +60 +80 +79 +75 +71 = 848 L sur 1 m2.
Surface de l'ouverture de la cavité : p r2 = 3,14 x 17,52 = 962 m2.
Volume d'eau de pluie qui s'infiltre en un an : 0,70 x 962 x848 =5,7 105 ~6 105 L..
2.
Dans la gamme de pH donnée, montrer que la masse maximale de
calcite qui peut être « dissoute » par litre d’eau de pluie est
de l’ordre de 0,3 g.
3 mmol / L à pH = 4,5 ; M(CaCO3) = 40,1 +12 +3 x16=100,1 g / mol.
3 x100,1 = 300,3 mg ~0,3 g / L.
|
|
Problème.
Estimer le nombre d’années nécessaires à la formation d’une cavité de
dimension semblable à celle du gouffre de Padirac. Commenter le
résultat obtenu.
Volume de la cavité cylindrique : V = p r2 h = 3,14 x 17,52 x 103 = 9,91 104 m3=9,91 107 L.
Masse de calcite dissoute : 9,91 104 x 2,7 × 103 = 2,68 108 kg.
Dans l'hypothèse d'une eau de pluie à pH = 4,5, volume d'eau nécessaire à cette dissolution :
2,68 108 / (0,3 10-3) = 8,9 1011 L.
Nombre d'années : 8,9 1011 / (6 105) ~1,5 106 ans.
La formation de telle cavité est très lente et s'étend sur des millions d'années.
|
|