Voyage dans
la ceinture d'astéroïdes, Bac S métropole 09/2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Dans
cet exercice, on étudiera le principe simplifié de la propulsion
ionique, puis dans une partie indépendante, on déterminera la masse de
l’astéroïde Cérès.
1. La propulsion ionique
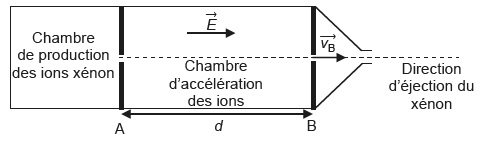
Les ions xénon créés sont accélérés entre les grilles A et B par un
champ électrique E supposé uniforme. À la sortie de la chambre
d’accélération, un dispositif appelé neutraliseur, transforme les ions
xénon en atomes de xénon, afin de maintenir la charge électrique
globale de la sonde Dawn constante.
1.1. Étude de l’ionisation du xénon
L’énergie d’ionisation d’un atome est l’énergie minimale nécessaire
pour arracher un électron de cet atome. Dans le cas du moteur ionique,
le mécanisme d’ionisation est fondé sur des processus physiques
complexes. On étudie ici un mécanisme plus simple au cours duquel le
xénon est ionisé par une radiation
lumineuse.
1.1.1. L’énergie
d’ionisation d’un atome de xénon est égale à 12,1 eV. Calculer la
valeur minimale de la longueur d’onde de la radiation qui permettrait
l’ionisation d’un atome de xénon en ion Xe+.
E =12,1 eV = 12,1 x 1,60 10-19 = 1,936 10-18 J.
l = hc / E = 6,63 10-34 x3,00 108 /(1,936 10-18) =1,03 10-7 m = 0,103 µm = 10,3 nm.
1.1.2. Dans quel domaine d’ondes électromagnétiques se situe cette radiation ? Justifier.
Cette valeur étant inférieure à 400 nm, la radiation appartient au domaine UV.
1.2. L’accélération des ions xénon
1.2.1. Montrer que la masse d’un atome de xénon vaut m = 2,18 × 10-25 kg.
m= M(Xe) / NA = 0,1313 / (6,02 1023) = 2,18 × 10-25 kg.
Pour la suite, on considèrera que la masse d’un atome de xénon est égale à la masse de l’ion xénon.
Les ions xénon Xe+, de masse m, pénètrent dans la chambre
d’accélération en A, avec une vitesse que l’on considèrera nulle. Une
tension électrique U constante est appliquée entre les grilles A et B.
1.2.2. Déterminer l’expression du travail WAB
de la force électrique F appliquée à un ion xénon se déplaçant de la
grille A à la grille B en fonction de e et U. On donne la relation
entre le champ électrique E, la tension U, et la distance d entre les
grilles A et B : E = U / d.
F = e E ; WAB = F d = e E d = e U.
1.2.3. La variation
de l’énergie cinétique des ions xénon entre les grilles A et B est
égale au travail de la force électrique sur ce trajet. En déduire que
la vitesse d’un ion xénon à la sortie de la chambre d’accélération est
donnée par la relation : vB =(2eU / m)½.
L'énergie cinétique initiale est nulle. La variation d'énergie cinétique est donc égale à ½mv2B = eU.
v2B =2 eU / m ; vB =(2eU / m)½.
1.2.4.
Déterminer, pour une tension accélératrice de 300 V, la valeur de la
vitesse d’éjection des ions xénon. Commenter la valeur obtenue.
vB = (2 x1,60 10-19 x 300 / (2,18 × 10-25))½ =2,1 104 m /s.
Cette valeur est très importante par rapport à la vitesse d'un véhicule ( voiture ).
1.3. Principe de la propulsion par réaction de la sonde spatiale
On désire illustrer le principe de la propulsion par réaction. On se
place dans un référentiel R dans lequel la sonde Dawn est initialement
immobile, dans une région de l'espace éloignée de tout astre. La masse
de la sonde Dawn, avant le démarrage du moteur ionique, est égale à Ms
= 1240 kg.
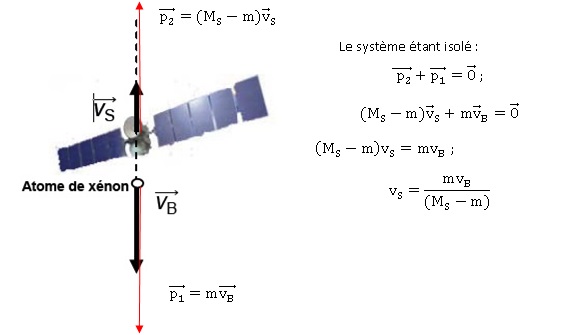
On étudie dans un premier temps l’éjection d’un seul atome de xénon, de vitesse vB par rapport au référentiel R. Après cette éjection, la sonde de masse (Ms – m), acquiert une vitesse vS par rapport à R.
1.3.1. Donner l’expression de la quantité de mouvement p1 de l’atome éjecté ainsi que la quantité de mouvement p2
de la sonde de masse (Ms – m) après l’éjection de l’atome de xénon. Le
schéma ci-contre représente la sonde Dawn ; les vecteurs vitesse sont
représentés sans souci d’échelle.
1.3.2. Dans la situation étudiée, justifier la conservation de la quantité de mouvement du système {sonde + atome de xénon}.
1.3.3. En déduire l’expression de vs en fonction de vB, Ms et m.
1.3.4. Calculer la valeur de vs et commenter le résultat. On prendra vB = 2,1 × 104 m.s-1.
vS =2,18 10-25 x2,1 104 / 1240 = 3,7 10-24 m /s, valeur très faible, quasiment nulle pour un ion éjecté.
Mais le moteur éjecte un grand nombre d'ions et non pas un seul ion.
En réalité, le moteur ionique éjecte en continu une grande quantité d’atomes de xénon : il consomme 3,3 mg de xénon par seconde.
1.3.5. La sonde Dawn a une réserve de 450 kg de xénon. Indiquer pendant combien d’années le moteur ionique peut fonctionner.
450 / (3,3 10-6) = 1,36 108 s soit environ 4,3 ans.
|
|
Les éléments chimiques du tableau ci-dessous ont été testés pour faire fonctionner des moteurs ioniques spatiaux.
Elément chimique
|
sodium
|
mercure
|
césium
|
argon
| krypton
|
xénon
|
énergie d'ionisation ( eV)
|
5,14
|
10,4 |
3,89 |
15,8 | 14,0
|
12,1
|
Propriétés
|
corrosif
|
corrosif, toxique
|
corrosif
|
inerte
|
inerte
|
inerte
|
1.3.6.
Bien que rare et cher, le xénon a été choisi comme gaz de propulsion du
moteur ionique de la sonde Dawn. À l’aide des données, indiquer deux
arguments pour justifier ce choix.
Le xénon est inerte et son énergie d'ionisation est inférieure à celle du krypton et de l'argon.
2. L’astéroïde Cérès
En 2015, la sonde Dawn s’est mise en orbite quasi-circulaire de rayon r
autour de l’astéroïde Cérès, astéroïde de rayon moyen R = 470 km. Ses
moteurs ioniques désactivés, la sonde Dawn a effectué une révolution
autour de Cérès à une altitude moyenne h= 13500 km en 15 jours à la
vitesse v.
Données :
Masse de Cérès : Mc = (9,46 ± 0,04) × 1020 kg.
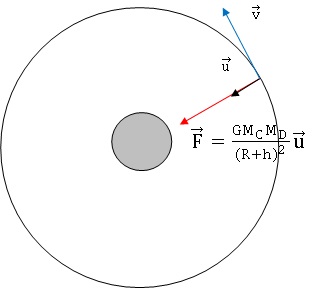
2.1. Donner les
caractéristiques de la force exercée par Cérès sur la sonde Dawn. Faire
un schéma représentant cette force. On notera MD la masse de la sonde Dawn.
La force est centripète.
|
|
|
|
2.2. Montrer que, dans le cas d’un mouvement circulaire, le mouvement de la sonde Dawn autour de Cérès est uniforme.
La sonde n'est soumise qu'à la force de gravitation exercée par Cérès ;
cette force est à chaque instant perpendiculaire à la vitesse. En
conséquence cette force ne travaille pas. L'énergie cinétique de la
sonde et donc la norme de sa vitesse sont constantes.
Le mouvement est uniforme.
2.3. Établir que la vitesse v de la sonde Dawn sur son orbite de rayon r autour de Cérès est donnée par la relation :
v = (GMc / r)½.
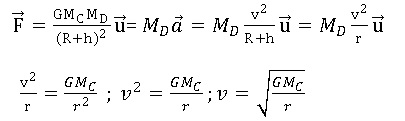
2.4. En déduire l’expression de la troisième loi de Kepler.
La sonde parcourt la circonférence 2 p r en T seconde à la vitesse v.
2p r = v T ; 4 p2 r2 = v2 T2 = GMC T2 / r ; T2 / r3 = 4 p2/ ( GMC).
2.5. Déterminer une valeur de la masse de l’astéroïde Cérès dans le cadre de l’hypothèse d’un mouvement circulaire. Commenter.
MC = r3 4 p2 / ( GT2).
r = (13500 + 470) 103 = 1,397 107 m.
T = 15 x24 x3600 = 1,296 106 s.
MC = (1,397 107)3 4 x3,142 / ( 6,67 10-11x(1,296 106 )2) =9,607 1020 kg.
Le texte indique : masse de Cérès : Mc = (9,46 ± 0,04) × 1020 kg.
La valeur trouvée présente une petite différence par rapport à celle
donnée dans le texte. Le mouvement de la sonde n'est pas tout à fait
circulaire.
|
|