Service et réception au Volley-ball, Bac S métropole 2018

Service et réception au Volley-ball, Bac S métropole 2018 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
	. .
	Après la course d'élan, le serveur saute de façon à frapper le ballon en un point B₀ situé à la hauteur h au-dessus de la ligne de fond de terrain. La hauteur h désigne l'altitude du centre du ballon. Le vecteur vitesse initiale v₀ du ballon est horizontal et perpendiculaire à la ligne de fond de terrain. L'instant de la frappe est choisi comme origine des temps. Le mouvement a lieu dans le plan (Oxy). On étudie le mouvement du centre du ballon, sans tenir compte de l'action de l'air, de la rotation du ballon sur lui-même et de ses déformations. 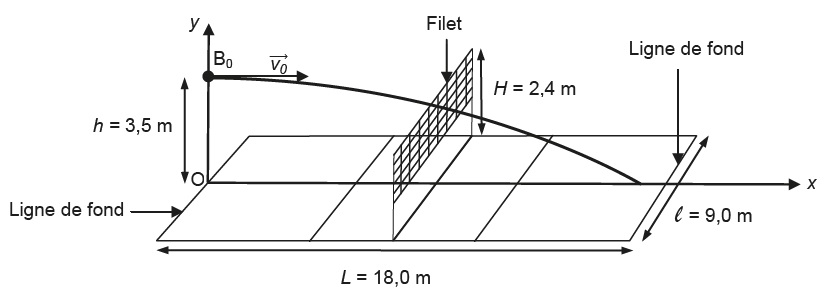Masse du ballon m = 260 g ; rayon du ballon : r = 10 cm. 1.Mesure de la vitesse initiale du ballon. Un radar portatif pointe en direction de B₀. Le radar envoie des ondes électromagnétiques haute fréquence ( f = 3,47 10¹⁰ Hz) 1.1. Identifier lle domaine des ondes électromagnétiques émises. Longueur d'onde : l = c / f = 3,0 10⁸ /(3,47 10¹⁰) ~8,6 10^-3 m. 1.2. Nommer le phénomène physique à l'origine de la différence de fréquence entre les ondes émises et rçue par le radar portatif. Effet Doppler. 1.3. Ce radar est positionné face au serveur et vise le ballon. La fréquence de l'onde reçue est-elle inférieure ou supérieure à celle de l'onde émise ? Justifier. Le ballon se rapproche du radar. La fréquence de l'onde reçue est supérieure à celle de l'onde émise. 1.4. Le décalage en fréquence est : \| Df\| = 2 v₀ f_émise / c = 4,86 kHz. En déduire v₀. v₀ =\| Df\| c / (2f_émise) = 4,86 10³ x3,00 10⁸ /(2 x3,47 10¹⁰) =21,0 m /s. 21,0 x 3,6 ~75,6 km / h. Le radar indique 76 km /h. Il y a donc accord entre ces deux valeurs.
	2. Validité du service. Le service est considéré comme valide à condition que le ballon franchisse le filet sans le toucher et qu'il retombe dans le terrain adverse. 2.1. Montrer que les coordonnées du vecteur accélération du centre du ballon sont a_x = 0 et a_y = -g. Le ballon n'est soumis qu'à son poids ( chute libre ). La seconde loi de newton conduit à : a_x = 0 et a_y = -g. 2.2. Etablir que les équations horraires du mouvement du centre du ballon s'écrivent : x = v₀t ; y = -½gt² +h. En déduire que l'équation de la trajectoire du ballon est y = -gx² /(2v₀²) +h. Le vecteur vitesse est une primitive du vecteur accélération et les coordonnées de la vitesse initiale sont ( v₀ ; 0). v_x = v₀ ; v_y = -gt. Le vecteur position est une primitive du vecteur vitesse et les coordonnées de la position initiales sont ( 0 ; h). x = v₀t ; y = -½gt² +h. t = x / v₀ ; tepport dans y : y = -gx² /(2v₀²) +h. 2.3. En admettant que le ballon franchisse le filet, vérifier qu'il touche le sol avant le ligne de fond. Quand le ballon touche le sol, son centre est à l'altitude r = 0,10 m. y = 0,10 = -gx² /(2v₀²) +h ; x =( 2v₀²(h-0,10) / g)^½ = ( 2 x 21,0² x3,40 / 9,81)^½ =17 m. Cette valeur est inférieure à L = 18 m. 2.4. Afin de déterminer la vitesse du ballon au moment où il touche le sol, on effectue une étude énergétique. L'origine de l'énergie potentielle est E_pp = 0 pour y = 0. 2.4.1. Rappeller les expressions des énergies cinétique, potentielle de pesanteur et mécanique du ballon en un point quelconque de la trajectoire. E_c = ½mv² ; E_pp = mgy ; E_m = ½mv² +mgy. 2.4.2. Le graphe suivant représente l'évolution en fonction du temps des trois énergies précédentes. Associer chaque courbe à l'une des énergies en justifiant. 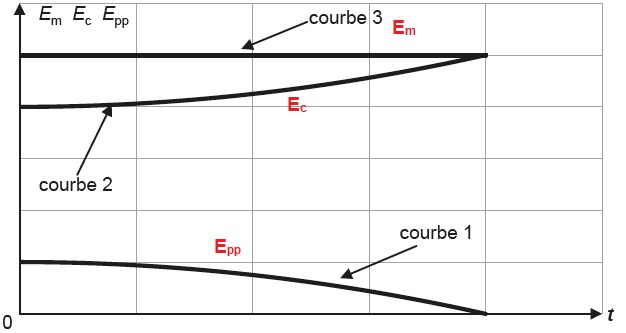Le ballon n'est soumis qu'à son poids, l'énergie mécanique est cconstante. L'énergie potentielle de pesanteur diminue : l'altitude du centre du ballon passe de la valeur 3,5 m à zéro. L'énergie cinétique initiale vaut ½mv₀² et croît de la diminution de l'énergie potentielle. 2.4.3. Déterminer la vitesse du ballon quand il touche le sol. Energie mécanique initiale : ½mv₀² + mgh. Energie mécanique finale : ½mv². Conservation de l'énergie mécanique : ½mv₀² + mgh = ½mv². v = (v₀² + 2g(h-r) )^½= (21² +2 x9,81 x3,4)^½ = 22,53 ~23 m /s.
	3. Réception du ballon par un joueur adverse. A l'instant initial, un joueur adverse est placé au niveau de la ligne de fond de son terrain. Il débute sa course vers l'avant pour réceptionner le ballon en réalisant une manchette. Le contact entre le joueur se fait au point R à une hauteur de 80 cm au dessus du sol. On admet que les équations horaires du mouvement du ballon restent valables. Evaluer la vitesse moyenne minimale du déplacement de ce joueur pour qu'il réalise la réception dans la position photographiée ci-dessus. Ce résultat semble-t-il réaliste ? Trajectoire du ballon est y = -gx² /(2v₀²) +h avec y =80 +10 = 90 cm = 0,90 m ( position du centre du ballon). x =(2 (h-y)v₀² / g)^½ = (2 x2,60)x21² / 9,81)^½=15,3 m. Le joueur adverse s'est déplacé de 18-15,3 = 2,7 m en t = x / v₀ =15,3 / 21 = 0,73 s. Sa vitesse moyenne est : 2,7 / 0,73 ~3,7 m /s ( 13 km /h). Cette valeur semble réaliste.