Mathématiques, probabilités, complexes, Bac S Liban 2018

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

Exercice 1. Probabilités ( 3 pts).
Les quinze jours précédents la rentrée universitaire, un standard téléphonique enregistre un nombre reccord d'appels. Les appelants sont mis en attente, entendent une musique et un message. Ce temps d'attente, exprimé en seconde, est modélisé par une variable aléatoire X qui suit une loi exponentielle de paramètre l = 0,02 s^-1. Ils sont ensuite mis en relation avec un chargé de clientèle qui répond à leurs questions. Le temps d'échange, exprimé en seconde, est modélisé par la variable aléatoire Y qui suit la loi normale d'espérance µ =96 s et d'écart type s =26 s.
1. Quelle est la durée moyenne d'un appel ( temps d'attente et temps d'échange) ?
1 / l + µ = 1 /0,02 + 96 = 50+96 =146 s.
2. Un étudiant est choisi au hasard parmi les appelants.
a. Calculer la probabilité que l'étudiant soit mis en attente plus de 2 minutes.
P(X > 120) = exp(-0,02 x120) = e^-2,4 ~ 0,091.
b. Calculer la probabilité pour que le temps d'échange soit inférieur à 90 s.
P( Y < 90) = 0,40874 ~0,409.
3. Une étudiante choisie au hasard parmi les appelants attend depuis plus d'une minute d'être mise en relation avec le service clientèle. Lasse, elle racroche et recompose le numéro. Elle espère attendre moins de 30 s cette fois-ci.
Le fait de raccrocher puis de rappeler augmente-t-il ses chances de limiter à 30 s l'attente supplémentaire ou bien aurait-elle mieux fait de rester en ligne ?
La loi exponentielle est à durée de vie sans vieillissement.

Exercice 2. Nombres complexes. ( 3 pts).
1. Donner les formes exponentielle et trigonométriques des nombres complexes 1+i et 1-i.
Module de ces nombres complexes(1+1)½ = 2^½.
(1+i) / |1+i| = 1 / 2^½ + i /2^½ = cos (p/4) + i sin (p/4).
1+i = 2^½( cos (p/4) + i sin (p/4)) = 2^½exp(ip/4).

(1-i) / |1-i| = 1 / 2^½ - i /2^½ = cos (-p/4) + i sin (-p/4).
1-i = 2^½( cos (-p/4) + i sin (-p/4)) = 2^½exp(-ip/4).
2. Pour tout entier naturel n, on pose S_n = (1+i)ⁿ +(1-i)ⁿ.
a. Déterminer la forme trigonométrique de S_n.
S_n = 2^0,5n [ exp(i n p/4)+exp(-i n p/4)]
Or exp(i n p/4)+exp(-i n p/4) = 2 cos(n p/4).
S_n = 2 x 2^0,5n cos(n p/4).
b. Pour chacune des deux affirmations suivantes, dire si elle est vraie ou fausse en justifiant.
- Pour tout entier naturel n, le nombre complexes Sn est un réel. Vrai.

n	0	1	2	3	4	5	6	7	8
n p / 4	0	p/4	p/2	3p/4	p	5p/4	3p/2	7p/4	2p
cos(n p / 4)	1	2^-½	0	-2^-½	-1	-2^-½	0	2^-½	1

Si n =4 k +2 avec k entier naturel, S_n =0.
Si n = 8 k ou n= 1 +8k ou n=7+8k, S_n= 2 x 2^0,5n cos(n p/4) ( cos 0 + i sin 0) est un réel strictement positif.
Si n = 3+8 k ou n= 4 +8k ou n=5+8k, S_n= 2 x 2^0,5n cos(n p/4) ( cos p + i sin p) est un réel strictement négatif.

- Il existe une infinité d'entiers naturels tels qu S_n = 0. Vrai.
Si n =4 k +2 avec k entier naturel, S_n =0.

Exercice 3. 4 pts..
On considère que deux sous-marins se déplacent en ligne droite, chacun à vitesse constante.
A chaque instant t, ( en minute), le premier sous -marin est repéré par le point S₁(t) et le second par un point S₂(t) dans un repère orthonormé dont l'unité est le mètre. La cote z est nulle au niveau de la surface de la mer et négative sous l'eau.
1. On admet que pour tout réel t > 0, S₁(t) a pour coordonnées :
x(t) = 140-60t ; y(t) = 105-90t ; z(t) = -170 -30t.
a. Donner les coordonnées du sous-marin en début d'observation.
x(t=0) = 140 ; y(t=0) = 105 ; z(t=0) = -170.
b. Quelle est la vitesse du sous marin ?
v_x = -60 ; v_y = -90 ; v_z = -30 ;
v₁ = [(-60)² +(-90)² +(-30)²]^½ =12600^½ =30 x 14^½ ~112,25 m / min.
2. On se place dans le plan vertical contenant la trajectoire du premier sous-marin. Déterminer l'angle a que forme la trajectoire du sous-marin avec le plan horizontal.
A l'instant initial, le sous-marin est au point A ( 140 ; 105 ; -170).
A t = 1, ce sous marin est au point B( 80 ; 15 ; -200).
On considère le point C ayant la même abscisse que B, la même ordonnée que B et la cote de A : C(80 ; 15 ; -170).

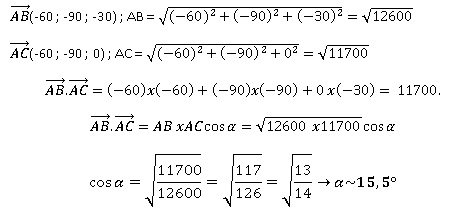
3. Au début de l'observation le second sous marin est situé au point S₂(0) de coordonnées (68 ; 135 ; -68) et atteint au bout de 3 minutes le point S₂(3) de coordonnées (-202 ; -405 ; -248) avec une vitesse constante. A quel instant t les deux sous marins sont-ils à la même profondeur ?
z₁(t) = -170 -30t.
v_z2 = -248+68 / 3 = -60 m / min.
z₂(t) = -60 t +Cste.
z₂(0) = 0+Cste = -68.
z₂(t) = -60 t -68.
z₁(t) =z₂(t) ; -170 -30t = -60 t -68.
30 t = 102 ; t = 102 / 30 = 3,4 min.

Exercice 4. Suites. 5 points.
On considère pour tout entier n >0 les fonctions f_n définies sur l'intervalle [1 ; 5 ) par : f_n(x) = ln(x) / xⁿ. On note C_n leurs courbes représentatives.

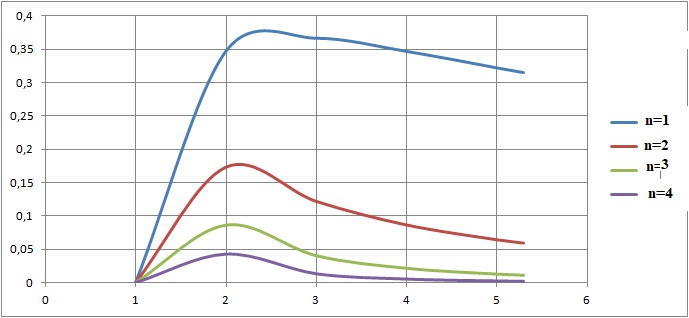
1. Montrer que pour tout entier n >0 et tout x réel de l'intervalle [1 ; 5 ], f_n'(x) = (1-n ln(x) )/ xⁿ⁺¹.
On pose u = ln(x) et v = xⁿ ; u' = 1 / x ; v' = n x^n-1.
(u'v-v'u) / v² =( x^n-1 - n x^n-1ln(x) ) / x²ⁿ = (1-n ln(x) )/ xⁿ⁺¹.
2. Pour tout n >0, on admet que la fonction f_n admet un maximum sur l'intervalle [1 ; 5 ]. On note A_n le point de la courbe C_n ayant pour ordonnée ce maximum.
Montrer que tous les points A_n appartiennent à une même courbe G d'équation : y = ln(x) / e.
La dérivée s'annule pour ln(x) = 1 / n soit x = e^1/n.
Ordonnée de A_n : y = ln(e^1/n) / e =ln(x) / e.
3.a. Montrer que pour tout entier n >1 et tout réel de [1 ; 5] : 0 < ln(x) / xⁿ < ln(5) / xⁿ.
ln(1) = 0 ; ln(5) positif.
La fonction logaritme est strictement croissante sur [1 ; 5 ].
0 < ln(x) < ln(5).
xⁿ est >1 sur [1 ; 5].
0 < ln(x) / xⁿ < ln(5) / xⁿ.
3.b. Montrer que pour tout entier n >1 :

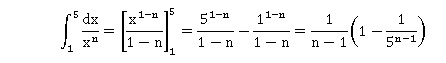
c. Pour tout entier n >0, on s'intéresse à l'aire sous la courbe C_n, c'est à dire l'aire du domaine plan délimitée par la courbe C_n et les droites d'équation x=1 et x = 5 et y = 0. Déterminer la valeur limite de cette aire quand n tend vers plus l'infini.
La fonction f_n étant le quotient de deux fonctions positives sur [1 ; 5 ], pour n >0, f_n est positive.
L'aire cherchée est : 1 / (n-1) [ 1-1 /(5^n-1].
Quand n tend vers plus l'infini :
5^n-1 tend vers zéro ; 1 / (n-1) tend vers zéro ; donc cette aire tend vers zéro.

Exercice 5. (5 pts).
Un jeu de hasard est paramétré de la façon suivante :
Si le joueur gagne une partie, la probabilité qu'il gagne la partie suivante est 0,25.
Si le joueur perd une partie, la probabilité qu'il perde la partie suivante est 0,5.
La probabilité de gagner la première partie est 0,25.
Pour tout entier n non nul, on note G_n l'événement " la n^ième partie est gagnée" et on note p_n la probabilité de cet événement. On a donc p₁ = 0,25.
1. Montrer que p₂ = 7 / 16.

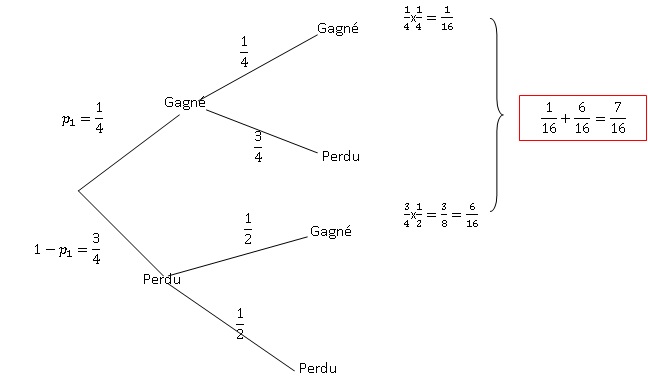
2. Montrer que pour tout entier n non nul, p_n+1 = -p_n / 4 +0,5.

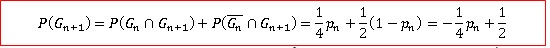
3. On obtient ainsi les premières valeurs de p_n :

n	1	2	3	4	5	6	7
p_n	1	0,4375	0,3906	0,4023	0,3994	0,4001	0,3999

Quelle conjecture peut-on émettre ?
La limite de p_n est 0,4.
4. On définit pour tout entier naturel non nul, la suite (u_n) par u_n= p_n-0,4.
a. Démontrer que cette suite est géométrique et donner la raison.
u_n+1= p_n+1-0,4= -p_n / 4 +0,5-0,4=0,1-p_n / 4 = (0,4-p_n) / 4 = -0,25 u_n.
La suite est géométrique de raison -0,25 et de premier terme p₁-0,4 = 0,25-0,4 = -3 / 20.
b. En déduire que pour tout entier naturel n non nul, p_n = 0,4 -3 / 20 (-0,25)^n-1.
u_n = -3 / 20 x (-0,25)ⁿ.
p_n = u_n +0,4 = 0,4 -3 / 20 (-0,25)^n-1.
c. La suite (p_n) converge t-elle ? Interpréter.
Quand n tend vers plus l'infini, (-0,25)^n-1 tend vers zéro et la suiteconverge vers 0,4.
Au bout d'un grand nombre de parties, la probabilité de gagner est de 0,4.