La mission
Proxima, Bac S Liban 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
A. A la rencontre de la station spatiale ISS.
Lors
du décollage du lanceur Soyouz, 4 propulseurs d'appoint assurent la
poussée pendant les deux premières minutes de vol avant d'être largués
par le lanceur. Au bout d'environ 10 minutes de vol, à une altitude de
près de 220 km, le module Soyouz est mis en orbite autour de la terre,
puis après des corrections d'orbitales, il rejoint l'orbite de la
station spatiale à une altitude d'environ 400 km.
L'étude est conduite dans le référentiel géocentrique.
RT = 6380 km ; altitude de l'orbite base du module Soyouz : hS = 220 km ; période de ce module sur son orbite basse TS = 88,66 min ; altitude de l'orbite haute Soyouz : HS = 320 km ; altitude de la station ISS : hISS = 400 km.
1. Orbites du module Soyouz et de l'ISS.
Au bout de 10 min de vol, le module Soyouz atteint son orbite basse considérée comme circulaire.
1.1.
Déterminer la valeur de sa vitesse VS sur son orbite basse.
La circonférennce 2 p(RT + hS) est décrite en TS seconde à la vitesse VS.
VS = 2 p(RT + hS) / TS = 2 x3,14 (6380+220) 103 / (88,66 x60)=7,7955 103 m /s ~7,80 km /s.
On considère que le module Soyouz et la station ISS ont des orbites circulaires.
1.2. Démontrer l'expression suivante :
TS2 / (RT +hS)3 = TISS2 / (RT +hISS)3 .
La troisième loi de Kepler s'écrit ( l'astre central étant la terre et les orbites étant circulaires ) :
TS2 / (RT +hS)3 =4p2 / (GMterre) pour Soyouz.
TISS2 / (RT +hISS)3 =4p2 / (GMterre) pour l'ISS.
1.3.. Déterminer la valeur de la vitesse VISS de la station ISS sur son orbite.
TISS =TS [(RT +hISS)/ (()RT +hS)]1,5=88,66 [(6380+400) / (6380 + 220) ]½ =92,311 ~92,3 min.
La circonférennce 2 p(RT + hISS) est décrite en TISS seconde à la vitesse VISS.
VISS = 2 p(RT + hISS) / TISS = 2 x3,14 (6380+400) 103 / (92,311 x60)=7,691 103 m /s ~7,69 km /s.
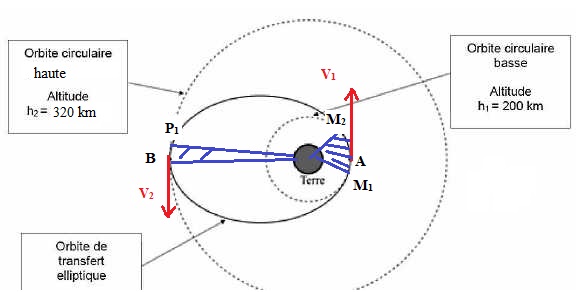
2. Orbite de transfert.
On s'interesse à une première
étape permettant à Soyouz de se trouver sur une orbite haute plus
proche de l'ISS. A un instant donné, lorsque Soyouz passe par le point
A de son orbite basse, on modifie la valeur de sa vitesse, sans changer
sa direction, jusqu'à la valeur V1. Soyouz suit alors une trajectoire elliptique appelée orbite de transfert.
Lorsque le module Soyouz arrive au point B de son orbite de transfert, il a une vitesse V2. On modifie alors la valeur de sa vitesse sans changer de direction jusqu'à la valeur finale VF qui permet au module de rester sur une orbite haute.
|
|
|
|
|
2.1. Enoncer la seconde loi de Kepler. En quoi cette loi permet-elle de montrer que V2 < V1 ?
Deuxième loi ou loi des aires :
le mouvement de chaque satellite est tel que le segment de droite
reliant le centre de la terre et le satellite balaie des aires égales
pendant des durées égales.
La distance M1 M2 est
inférieure à la distance P1 B.
Les durées de parcours entre les
points M1 et M2 puis P1 et B sont égales.
Donc la vitesse moyenne entre les points M1 et
M2 est supérieure
à celle entre les points P1 et B.
L'expression de l'énergie potentielle EP de Soyouz, définie à une constante près, est la suivante :
EP = -G m Mterre / (RT+h) avec m : masse du module Soyouz.
2.2 Montrer que EP(B) > EP(A).
EP(B) = -G m Mterre / (RT+HS).
EP(A) = -G m Mterre / (RT+hS).
Or hS < HS, donc G m Mterre / (RT+hS) > G m Mterre / (RT+HS).
-EP(A) > - EP(B) soit : EP(A) < EP(B)
2.3.
Justifier que l'énergie mécanique du module Soyouz sur son orbite de transfert entre les points A et B ne varie pas.
Soyouz
n'est soumis qu'à la force de gravitation exercée par la terre. Cette
force étant conservative, l'énergie mécanique de Soyouz reste constante
sur l'orbite de transfert.
2.4
En déduire si la variation d'énergie cinétique entre A et B est
positive ou négative. Ce résultat est-il en accord avec la seconde loi
de Kepler ?
Energie mécanique en A : EP(A) +EC(A).
Energie mécanique en B : EP(B) +EC(B).
Conservation de l'énergie mécanique : EP(A) +EC(A)= EP(B) +EC(B).
Variation d'énergie cinétique : EC(B) -EC(A) = EP(A) - EP(B)
Or EP(A) < EP(B), donc EC(B) -EC(A) et donc VB < VA.
En accord avec la seconde loi de Kepler.
2.5. Exprimer l'énergie mécanique de Soyouz au point A en fonction de m, G, Mterre, hS, RT et V1.
-G m Mterre / (RT+hS) + ½mV12.
2.6. Sachant que V1 = 7,80 103 m /s, déterminer la valeur de V2. Ce résultat est-il en accord avec les résultats précédents ?
-G m Mterre / (RT+hS) + ½mV12= -G m Mterre / (RT+HS) + ½mV22.
-2G Mterre / (RT+hS) + V12= -2G Mterre / (RT+HS) + V22.
V22= 2G Mterre [ 1/ (RT+HS) -1 / (RT+hS) ]+ V12 ;
V22= 2x6,67 10-11x5,98 1024 [ 1/ (6,7 106) -1 / (6,6 106) ]+ (7,8 103)2 ~5,9 107 ; V2 ~ 7,68 103 m /s.
En accord avec les résultats précédents.
3. Que faut-il faire ensuite pour que le module Soyouz atteigne la station ISS ?
Il faut effectuer de nouvelles corrections d'orbitales.
|
|
B. Echographe télé-opéré. .
4. Ondes ultrasonores.
Les ondes sonores ou ultrasonores sont des ondes mécaniques longitudinales.
4.1. Préciser la signification du mot longitudinale.
La direction de propagation de l'onde et la direction de la déformation du milieu sont identiques.
4.2 Citer une différence qui existe entre une onde ultrasonore et une onde sonore.
L'onde sonore est perçue par l'oreille humaine alors que l'onde ultrasonore ne l'est pas.
Les fréquences des ondes sonores sont comprises ent 20 Hz et 20 kHz.
Les fréquences des ondes ultrasonores sont supérieures à 20 kHz.
La mesure de la célérité des ondes ultrasonores dans un milieu donné peut être rélisée en laboratoire.
Un émetteur d'ultrasons et situé à une distance d d'un récepteur d'ultrasons.
A l'instant t = 0, l'émetteur émet une salve ultrasonore.
.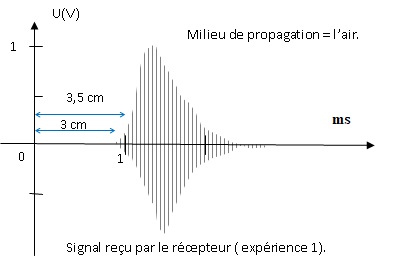
4.3. Déterminer la valeur du retard entr e l'émission et la réception.
3 / 3,5 x1 = 0,857 ms.
4.4 Sachant que d = 30,0 cm, en déduire la célérité des ondes ultrasonores dans ce milieu.
0,300 / (0,857 10-3 )~ 3,5 102 m /s.
4.5. Commenter le résultat en ragard du milieu de propagation.
Ce résultat est en accord avec la célérité des ultrasons dans l'air.
5. Principe de l'échographie.
L'émetteur et le récepteur sont placés côte à côte, face à un écran réfléchissant. L'origine des temps est celui de l'émission.
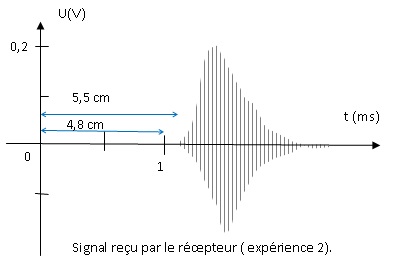
Déterminer la valeur de la distance émetteur - écran.
Le signal effectue un aller et retour émetteur-écran dans l'air durant 5,5 / 4,8 ~1,15 ms.
Distance émetteur-écran : 350 x1,15 10-3 / 2 ~ 0,20 m.
6. Application à l'échographie.
La sonde envoie des ultrasons dans le corps du patient qui sont
réfléchis à chaque fois qu'ils rencontrent un changement de milieu. Ces
échos sont reçus par la même sonde.
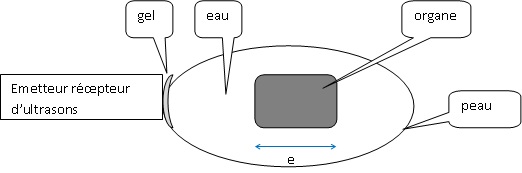
L'épaisseur de gel est négligeable. µs.
A l'instant t=0, la sonde émet des ultrasons. On visualise deux échos aux dates t1 = 100 µs et t2 = 150 µs.
6.1. A quoi correspondent ces deux échos ?
Réflexion sue l'avant de l'organe et réflexion sur la partie arrière de l'organe.
6.2 Sachant que la célérité des ultrasons dans l'organe est corgane =1,54 103 m /s, déterminer la taille de l'organe.
Soit d l'épaisseur d'eau traversée et ceau la célérité des ultrasons dans l'eau.
2d = ceau t1.
2e =corgane( t2- t1) ; e = 1,54 103 x 50 10-6 / 2 =3,85 10-2 m.
|
|