Mathématiques,
probabilités, géométrie dans l'espace,
Bac S Inde 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Exercice 3 ( 5 points).
Une
entreprise conditionne du sucre blanc provenant de deux exploitations U
et V en paquets de 1 kg de différentes qualités. Le sucre extra fin est
conditionné séparément dans des paquets portant lz label " extra fin".
Partie A.
Pour
calibrer le sucre en fonction de la taille des cristaux, on le fait
passer à traavers une série de trois tamis positionnés les uns au
dessous des autres et posés sur un récipient à fond étanche. Les
ouvertures des mailles sont : 0,8 mm, 0,5 mm et 0,2 mm.
1.
On prélève au hasard un cristal de sucre de l'exploitation U. La taille
de ce cristal ( en mm) est modélisée par une variable aléatoire XU qui suit une loi normale de moyenne µU = 0,58 mm et d'écart type sU = 0,21 mm.
a. Calculer les probabilités des événements suivants : XU < 0,2 et 0,5 < XU < 0,8.
P(XU < 0,2 )= 0,035.
P(XU < 0,5) = 0,35162 ; P(XU < 0,8 )= 0,8526 ; P(0,5 < XU < 0,8) =0,8526-0,35162 =0,501.
b.
On fait passer 1800 g de sucre provenant de l'exploitation U au travers
la série de tamis. Déduire de la question précédente une estimation de
la masse de sucre récupée dans le tamis 2 et la masse de sucre extra
fin.
Sucre extra fin : 1800 x 0,035 = 63 g.
Sucre recueilli dans le tamis 2 : 1800 x0,501 ~902 g.
3.
On prélève au hasard un cristal de sucre provenant de l'exploitation V.
La taille de ce cristal ( en mm) est modélisé par la variable aléatoire
XV qui suit la loi normale de moyenne µV = 0,65 mm et d'écart type sV à déterminer. Lors du calibrage, 40 % des cristaux sont dans le tamis 2. Calculer l'écart type sV.
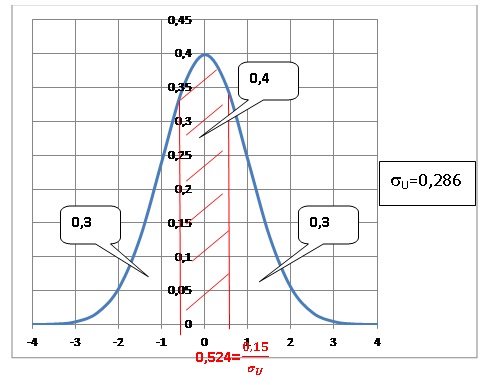
P(0,5 < XV < 0,8) = 0,4.
On pose Y = (XV-0,65) / sV. Y suit la loi normale centrée réduite N(0 ; 1).
P((0,5-0,65) / sV < Y < (0,8-0,65) / sV) = 0,4.
P((-0,15) / sV < Y < (0,15) / sV) = 0,4.
Partie
B.
On admet que 3% du sucre provenant de l'exploitation U est ultra fin et
que 5 % du sucre provenant de l'exploitation V est ultre fin.On prélève
au hasard un paquet dans la production et on s'intéresse à sa
provenance. On considère les événements :
U : le sucre provient de l'exploitation U.
V : le sucre provient de l'exploitation V.
E : le sucre est ultra fin.
1. Dans
cette question, on admet que 30 % du sucre provient de l'exploitation U
et le reste de l'exploitation V, sans mélange des sucres.
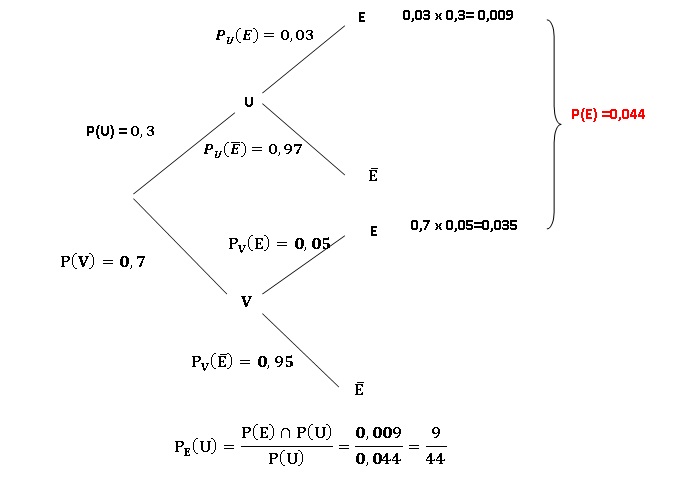
a. Quelle est la probabilité que le paquet porte le label extra fin ?
b. Sachant que le paquet porte le label extra fin, quelle est la probabilité que le sucre provienne de l'exploitation U ?
 . .
|
|
|
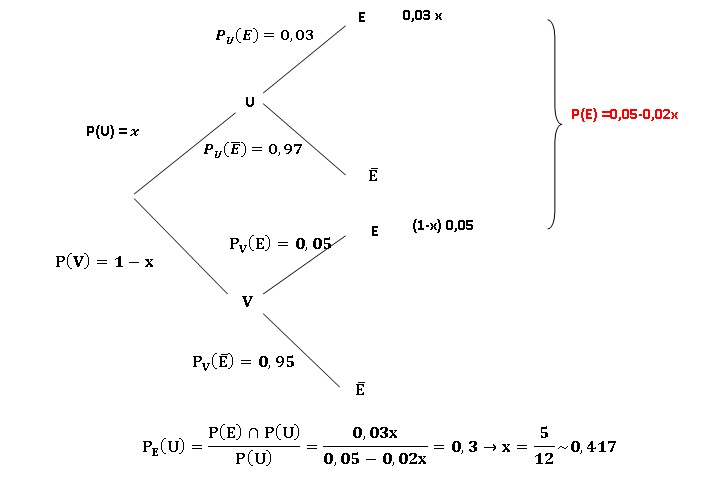
2.
L'entreprise souhaite modifier son approvisionnement auprès des deux
fournisseurs afin que parmi les paquets portant le label extra fin, 30
% du sucre provienne de l'exploitation U. Comment doit-elle
s'approvisionner auprès des exploitants U et V ?
Partie C.
1. L'entreprise
annonce que 30 % des paquets de sucre portant le label extra fin
contiennent du sucre provenant de l'exploitation U. Un acheteur veut
vérifier cette proportion. Ilprélève 150 paquets pris au hasard dans la
production de paquets labellisés extra fin. Parmi ces paquets, 30
contiennent du sucre provenant de l'exploitation U.
A t-il raison de remettre en question l'annonce de l'entreprise ?
On répète n = 150 fois le prélevement de manière indépendante.
30 % des paquets labellisés extra fin proviennet de U : p =0,3 ; q = 1-p = 0,7.
n > 30 ; np = 45 > 5 et nq =105 > 5.
On peut définir un intervalle de fluctuation asymptotique au seuil de 95 %.
(pq / n )½ = (0,3 x0,7 / 150)½ ~0,0374 ; 1,96 x0,0374 ~0,073.
[p-0,073 ; p +0,073] soit [0,227 ; 0,373].
30 / 150 = 0,2 n'appartient pas à cet intervalle. Au seuil de 95 %, on rejette l'affirmation.
2. L'année suivante
l'entreprise déclare avoir modifié sa production. l'acheteur souhaite
estimer la nouvelle proportion de paquets de sucre provenant de
l'exploitation U parmi les paquets portant le label extra fin. Il
prélève au hasard 150 paquets labellisés extra fin. 42 % contiennent du
sucre provenant de l'exploitation U.
Donner un intervalle de confiance, au niveau de confiance de 95 %, de
la nouvelle proportion de paquets labellisés extra fin contenant du
sucre provenant de l'exploitation U.
n = 150 ; fréquence f = 0,42 ; 1-f = 0,58.
.n > 30 ; nf = 63 > 5 et n(1-f) =87 > 5.
Les conditions sont requises pour établir un intervalle de confiance.
n-½ = 150-½~0,0816. ; -2).
[f-0,0816 ; f +0,0816) soit :[0,339 ; 0,501].
|
|
|
|
|
Exercice 4 ( 5 points).
Dans l'espace muni d'un repère orthonormé, on considère les points A (2 ; 1 ; 4), B(4 ; -1 ; 0), C(0 ; 3 ; 2) et D(4 ; 3 ; -2).
1. Donner une représentation paramétrique de la droite (CD).
Coordonnées du vecteur directeur de cette droite :
(4-0 ; 3-3 ; -2-2) soit (4 ; 0 ; -4) ou plus simplement ( 1 ; 0 ; -1)
Par suite x = t+a ; y = b, z = -t+c avec t réel.
La droite passe par le point C :
x = t ; y = 3, z = -t+2 avec t réel.
2. Soit M un point de la droite (CD).
a. Déterminer les coordonnées de M(x ; y ; z) afin que la distance BM soit minimale.
Coordonnées du vecteur BM : ( t-4 ; 3+1 ; -t+2).
BM2 = [(t-4)2 +42+(-t+2)2]=[t2+16-8t+16+t2+4-4t] =2t2-12t+36.
Ce polynome du type ax2+bx+c, avec a >0,admet un minimum pour x = -b/(2a)=12 / 4 = 3.
M( 3 ;3; -1).
b. On note H (3 ; 3 ; -1) un point de la droite (CD). Vérifier que les droites ( BH) et (CD) sont perpendiculaires.
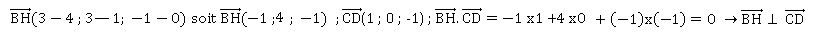
c. Montrer que l'aire du triangle BCD est égale à 12 cm2.
BH = (1+4+1)½ = 18½ ; CD =(42 +0+(-4)2)½=32½.
Aire de ce triangle : BH x CD / 2 = (18 x32)½ / 2 = 24 / 2 = 12 cm2.
3. Démontrer que le vecteur de coordonnées (2 ; 1 ; 2) est normal au plan (BCD).
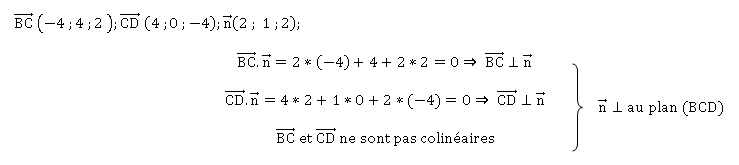
Déterminer une équation cartésienne de ce plan.
2x +y+2z +d = 0.
C appartient à ce plan : 0 +3 +2*2 +d = 0 ; d = -7.
2x +y+2z -7 = 0.
Déterminer une représentation paramétrique de la droite D passant par A et orthogonale au plan ( BCD).
x = 2t+a ; y = t +b ; z = 2t+c.
La droite passe par A :x = 2t +2 ; y = t+1 ; z = 2t+4.
Démontrer que le point I, intersection de la droite D et du plan (BCD) a pour coordonnées (2 /3 ; 1 / 3 ; 8 /3).
2(2t+2) +t+1 +2(2t+4)-7=0.
4t+4+t+1+4t+8-7=0 ; t = -6 /9 = -2 /3.
I( -4 / 3 +2 ; -2 / 3 +1 ; -2/3 *2+4) soit (2 /3 ; 1 / 3 ; 8 /3).
4. Calculer le volume du tétraèdre ABCD.
D perpendiculaire au plan ( BCD) en I et passe par A.
AI hauteur du tétraèdre de base BCD.
AI =[(2/3-2)2 +(1/3-1)2+(8/3-4)]½ =2 cm.
V =hauteur x aire de la base BCD / 3 = 2 x 12 / 3 = 8 cm3.
|
|
|