Mathématiques,
fonction, nombres complexes,
Bac S Inde 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Exercice
1 ( 6 points).
Dans une usine, un four cuit des céramiques à la température de 1000
°C. A la fin de la cuisson, il est éteint et refroidit. On s'intéresse
à la phase de refroidissement du four, qui débute à l'instant où il est
éteint. La porte du four peut être ouverte sans risque pour les
céramiques dès que sa température est inférieure à 70°C.
Partie A.
On note Tn la température du four au bout de n heures
écoulées à partir de l'instant où il est éteint. On a donc T0
= 1000 °C. Tn est calculée par l'algorithme suivant :
T <--- 1000.
Pour i allant de 1 à n
T <---0,82 T+3,6
Fin Pour.
1. Déterminer la température du
four, arrondie à l'unité près, au bout de 4 heures de refroidissement.
T1 = 820 +3,6=823,6 °C.
T2 = 0,82 x823,6 +3,6 = 678,952 °C
T3 = 678,952 x0,82 +3,6 =560,34°C.
T4 = 560,34 x 0,82 +3,6 =463,1 ~463°C.
2. Démontrer que
pour tout entier n, on a : Tn = 980 x0,82n +20.
Initialisation
: T1 = 980 x0,82 +20 = 823,6°C.
Hérédité :
la propriété est supposée vraie au rang p : Tp = 980 x0,82p +20.
Tp+1 = 0,82 Tp +3,6 =0,82 x980 x0,82p
+20 = 980 x0,82p+1 +20. La propriété
est vraie au rang p+1.
Conclusion
: la propriété est vraie au rang 1 et héréditaire, elle est donc vraie
pour tout n.
3.
Au bout de combien d'heures le four peut-il être ouvert sans risque
pour les céramiques ?
70 > 980 x0,82n +20 ; 50 / 980 > 0,82n ;
ln(50 / 980) > n
ln(0,82) ; n >
14,99 ; n >15 heures.
Partie
B.
On note t le temps en heures écoulé depuis l'instant où le four est
éteint. La température du four est donnée par f(t) = a exp(-t /
5) +b, pour tout t positif ; a et b sont deux nombres réels. On admet
que f vérifie la relation suivante : f '(t) +f(t) / 5 = 4.
1 Déterminer
a et b.
f '(t) = -a / 5 exp(-t/5) ; f(0) = 1000 ; f '(0) = -a / 5 ; -a /
5 +1000 / 5 = 4 ; a = 980.
f(0) = 1000 = a exp(0) +b = 980 +b ; b
= 20.
Pour la suite, on admet que f(t) = 980 e(-t/5) +20.
2.a. Déterminer la
limite de f quand t tend vers l'infini.
Le terme en exponentielle tend vers zéro si t tend vers plus l'infini ;
f(t) tend donc vers 20°C quand
t tens vers plus l'infini.
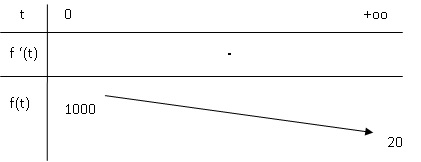
2.b. Etudier les
variations de f et en déduire son tableau de variations..
f '(t) = -980 / 5 exp(-t/5) =
-196 exp(-t/5).
Le terme en exponentielle étant toujours positif, f '(t) est négative
et f(t) est strictement décroissante.
2.c. Avec ce
modèle, après combien de minutes le four peut-il être ouvert sans
risque pour les céramiques ?
980 e(-t/5)
+20 < 70 ; e(-t/5)
< 50 /
980 ; -t / 5 <
ln(50 / 980) ; t >
5 ln(980 / 50) ; t >14,8776
heures soit environ 893 minutes.
|
|
|
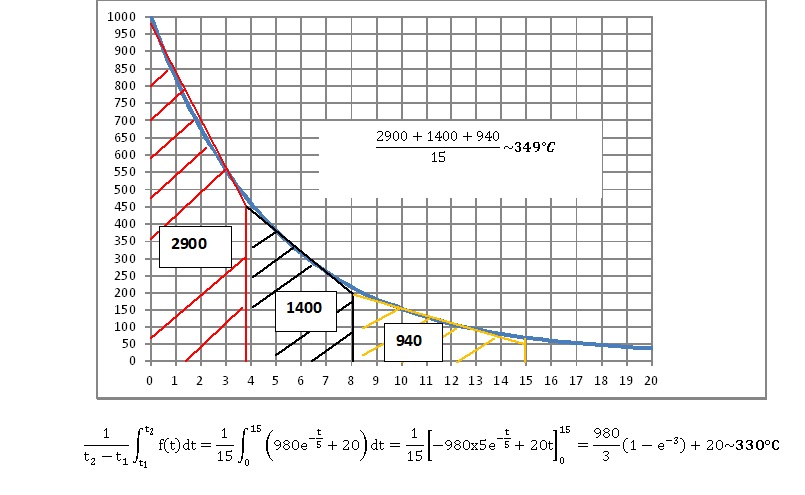
3. La température moyenne du four
entre les instants t1 et t2 est donnée par la
relation ci-dessous :
Détermier graphiquement la température moyenne du four sur les 15
premières heures de refroidissement.
Calculer la valeur exacte de cette température moyenne et en donner une
valeure arrondie au degré Celsius près.
4. Dans cette
question, on s'interesse à l'abaissement de la température du four au
cours d'une heure. Cet abaissement est donné par : d(t) = f(t)-f(t+1)
pout t positif.
a. Vérifier que
d(t) = 980 (1 -exp(-1 / 5) exp(-t /5).
f(t) = 980 exp(-t / 5) +20 ; f(t+1) = 980 exp((-t+1) / 5) +20= 980
exp(-t / 5) exp(-1 /5) +20.
d(t) = 980exp(-t/5) exp(-1/5) - 980 exp(-t / 5) = 980 exp(-t / 5)
[1-exp(-1/5)].
b. Déterminer la
limite de d(t) quand t tend vers l'infini. Interpréter.
exp(-t/5) tend vers zéro quand t tend vers plus l'infini. Donc d(t)
tend vers zéro quand t tend vers l'infini.
Au bout d'un temps suffisamment long, la température se stabilise à
20°C.
|
|
|
|
Exercice 2 (4 points).
Les points A, B et C ont pour affixe
respectives a = -4, b = 2 et c = 4.
1. On considère
trois points A', B' et C' d'affixes respectives a' = ja, b' = jb
et c' = jc où j = 0,5(-1 +i 3½).
a. Donner la forme
trigonométrique et le forme exponentielle de j. En déduire les formes
algébrique et exponentielle de a', b' et c'.
Module de j : |j| = 0,5((-1)2 + 3)½ =1.
j / |j| = -0,5 +i 3½ /2 = cos ( 2p/3 )+ i sin (2p/3) = exp(2i p/3).
a' = 2(1 -i 3½)= -4exp(2i p/3).
b'= -1 +i 3½= 2exp(2i p/3).
c'= 2(-1 +i 3½)= 4exp(2i p/3).
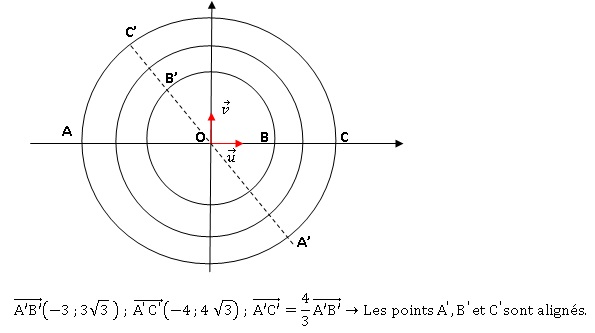
b. Les points A, B et C ainsi que
les cercles de centre O et de rayons 2, 3 et 4 sont représentés sur le
graphique suivant. Placer les points A', B' et C' sur ce graphique.
2. Montrer que les
points A', B' et C' sont alignés.
3. On note M le
milieu du segment [A'C], N le milieu du segment [CC'] et P le milieu du
segment [C'A]. Démontrer que le triangle MNP et isocèle.
M ( (2+4)/2 ; (-3½) soit M(3 ; -3½).
N( (4-2) / 2 ; 3½) soit N( 1 ; 3½).
P((-2-4) / 2 ; 3½) soit P( -3 ; 3½).
MN =( (1-3)2 + (3½+3½)2)½
=(4 +12)½ = 4.
PM =( (-3-3)2 + (-3½-3½)2)½
=(36 +12)½ = 4 x3½.
PN =( (-3-1)2 + (3½-3½)2)½
=(16 +0)½ = 4.
PN = MN = 4. Le triangle MNP est isocèle en N.
|
|
|