Mathématiques,
géométrie dans l'espace, Bac S Centres
étrangers 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Exercice 4
( 5 points ).
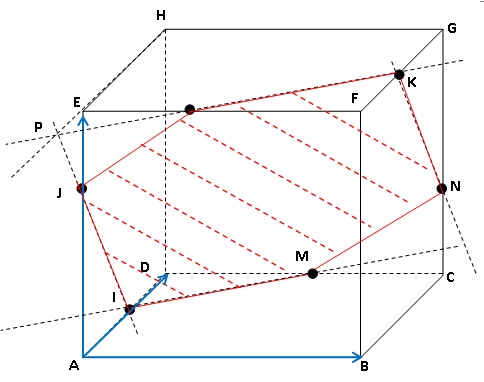
La figure ci-dessous représente un cube.
I est le milieu du segment [AD].
J est tel que AJ ) 0,75 AE.
K est le milieu du segment [FG]
Partie A.
1. Construire sans justifier la point d'intersection P du plan ( IJK) et de la droite (EH).
2. En déduire en justifiant l'intersection du plan (IJK) et du plan ( EFG).
La droite (EH) est incluse dans le plan (EFG) et P est l'intersection du plan (IJK) et de la droite (EH).
De plus le point K appartient aux deux plans.
L'intersection de ces deux plans est la droite (PK).
Partie B.
1. a. Donner sans justification les coordonnées des points I, J et K.
I( 0 ; 0,5 ; 0) ; J(0 ; 0 ; 0,75) ; K ( 1 ; 0,5 ; 1).
1.b. Déterminer les réels a et b tels que :
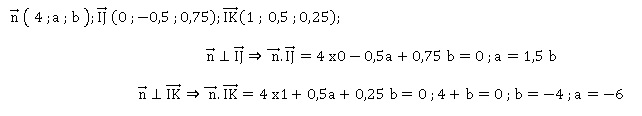
1.c. En déduire qu'une équation cartésienne du plan (IJK) est : 4x -6y -4z +3=0.
Equation cartésienne de ce plan 4x -6y -4z +d = 0.
I appartient à ce plan : 4 x0 -6 x0,5 -4x0 +d = 0 ; d =3.
2.a. Donner une représentation paramétrique de la droite (CG).
C( 1 ; 1 ; 0) ; G( 1 ; 1 ; 1).
Coordonnées du vecteur CG : (0 ; 0 ; 1)
Cette droite passe par le point C.
x = 1 ; y = 1 ; z = t avec t réel.
b. Calculer les coordonnées du point N, intersection de la droite (CG) et du plan (IJK).
N appartient à la droite (CG).
xN = 1 ; yN = 1.
N apppartient au plan(IJK) :
4 xN -6yN -4zN +3 =0 ;
4-6-4zN+3 = 0 ; zN = 0,25.
N(1 ; 1 ; 0,25).
c. Placer N sur la figure et construire en couleur l'intersection du cube par le plan (IJK).
.
|
|
|
|
|
Partie C.
On note R le projeté orthogonal du point F sur le plan (IJK).
On définit l'intérieur du cube comme l'ensemble des points M(x ; y ; z) tels que :
0 < x <1 ; 0 < y < 1 ; 0 < z < 1.
Le point R est-il à l'intérieur du cube ?
La droite (FR) est perpendiculaire au plan (IJK).
Le vecteur n(4 ; -6 ; 4) est orthogonal à ce plan. Ce vecteur est donc un vecteur directeur de la droite ( FR).
La droite passe par F( 1 ; 0 ; 1).
Représentation paramétrique de cette droite : x = 4t +1 ; y = -6t ; z = -4t+1 avec t réel.
Rappartient au plan : 4 xR -6yR -4zR +3 =0 ;
R appartient à la droite (FR) :
xR = 4t +1 ; yR = -6t ; zR = -4t+1.
16t +4+36t + 16t-4+3 = 0 ; 68 t = -3 ; t = -3 /68.
xR = -3 /17+1 = 14 / 17 ; yR = 9 / 34; zR =3 / 17+1 = 20 / 17.
zR est supérieur à 1, R est à l'extérieur du cube.
|
|