Mathématiques,
probabilités, suites, Bac S Centres
étrangers 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Exercice 3
( 7 points ).
Un détaillant étudie l'évolution de la vente de melons.
Partie A.
Les melons se vendent bien lorsque leur masse est comprise entre 900 g
et 1200 g. De tels melons sont qualifiés " conformes".
Les melons sont achetés auprès des maraîchers A, B et C.
Pour les melons de A, on modélise la masse en gramme par une variable
aléatoire MA qui suit la loi uniforme sur l'intervalle [850
; x] avec x réel > 1200.
Pour les melons de B, on modélise la masse
en gramme par une variable aléatoire MB qui suit la loi
normale de moyenne 1050 et d'écart type inconnu s.
C affirme que 80 % de ses melons sont conformes.
1. 75 % des melons
de A sont conformes. Déterminer x.
P( 900 < MA
< 1200
) =0,75 ;
(1200 -900 / (x-850) = 0,75 ; 300 = 0,75x -637,5
0,75 x = 937,5 ; x = 1250.
2. 85 % des melons
fournis par B sont conformes. Déterminer l'écart type s.
On pose Z = (MB-1050) / s. Z suit la loi normale
centrée réduite N(0 ; 1).
P(900 < MB < 1200) = 0,85.
P((900-1050) / s < Z < (1200-1050) / s) = 0,85.
P(-150 / s < Z < 150 / s) = 0,85.
2 F(150 / s)-1 = 0,85.
F(150
/ s) = 1,85 / 2 =
0,925.
P(Z < 150 / s) = 0,925.
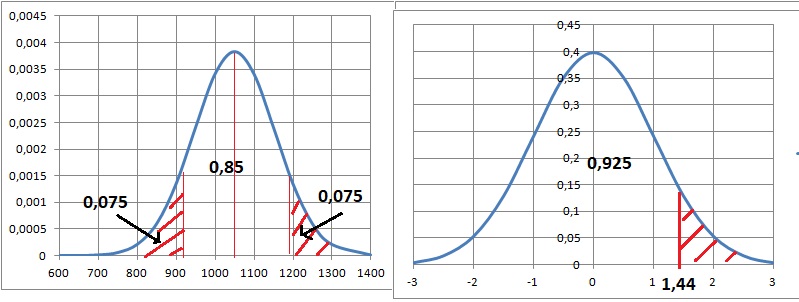
150 / s =1,44 ; s= 104.
3.
On doute de l'affirmation de C. On constate que sur 400 melons livrés
par C, seulement 294 sont conformes. A t-on raison de douter ?
Fréquence observée des melons conformes : 294 / 400 = 0,735.
On teste l'hypothèse p = 0,80.
n = 400 > 30 ; np
=320 > 30 ; n(1-p)
= 80 > 30.
Les conditions sont remplies pour définit un Intervalle de fluctuation
asymptotique au seuil de 95 %.
1,96 [(p (1-p) / n )]½ = 1,96 (0,8 x0,2 / 400)½
=0,0392.
[0,8-0,039 ; 0,8 +0,039 ) soit [0,76 ; 0,84].
f = 0,735 n'appartient pas à cet intervalle. L'affirmation de C est
fausse au risque de 5 %.
.
|
|
|
|
|
Partie B.
Une étude sur les clients donne :
- parmi les clients qui achètent un melon une semaine donnée, 90 %
d'entre eux achètent un melon la semaine suivante.
- parmi les
clients qui n'achètent pas de melon une semaine donnée, 60 % d'entre
eux n' achètent pas de melon la semaine suivante.
On choisit au hasard un client ayant acheté un melon au cours de la
semaine 1 et, pour n >
1 on note An l'événement : " le client achète un melon au
cours de la semaine n". Ainsi P(A1) = 1.
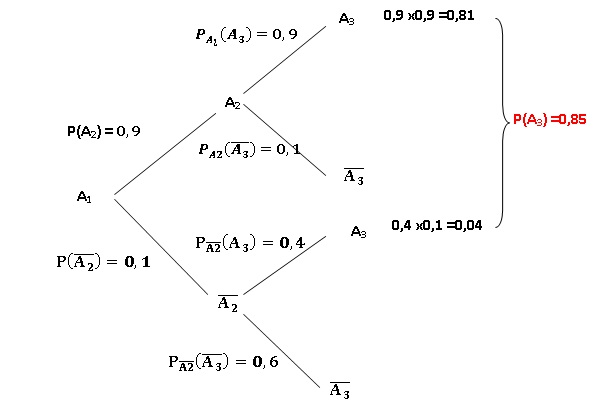
1.a. Compléter
l'arbre de probabilités suivant.
b. Démontrer que P(A3)
= 0,85.
c. Sachant que le client achète un
melon la semaine 3, quelle est la probabilité qu'il en ait acheté un au
cours de la semaine 2 ?
PA3(A2)=P(A2) n P(A3) / P(A3)
=0,9 x0,9 / 0,85 = 0,95.
|
|
On pose pour tout entier
n >1, pn = P(An). Ainsi p1 = 1.
2. Démontrer que
pour tout entier n >
1 : pn+1 = 0,5 pn +0,4.
Formule des probabilités totales : pn+1 = P(An n An+1) + P(non An n An+1)=0,9 pn+0,4(1-pn) = 0,5 pn +0,4.
3. a. Démontrer par récurrence
que pour tout entier n >
1, pn >0,8.
Initialisation : p1 = 1 > 0,8 est vraie.
Hérédité : pn > 0,8 est supposé vrai.
pn+1 = 0,5 pn +0,4 > 0,5 x0,8 +0,4 ; pn+1 >0,8.
Conclusion : La propriété est vrai au rang 1 et héréditaire ; elle est vraie pour tout entier n > 1.
3.b. Démontrer que
la suite (pn) est décroissante.
pn+1-pn = 0,5 pn +0,4 -pn = 0,4 -0,5pn= (0,8-pn ) / 2.
Or pn > 0,8 donc 0,4 -0,5pn < 0.
pn+1-pn < 0, la suite (pn) est décroissante.
3.c. La suite (pn)
est-elle convergente ?
La suite est décroissante et minorée par 0,8, donc elle converge.
4. On pose pour
tout entier n >1 :
vn = pn-0,8.
a. Démontrer que la
suite ( vn) est géométrique. Donner le premier terme et la
raison.
vn+1 = pn+1-0,8 = 0,5 pn +0,4 -0,8 = 0,5 pn -0,4 = (pn-0,8) x0,5 = 0,5 vn.
v1 = p1-0,8 = 1-0,8 = 0,2.
La raison est égale à 0,5.
b. Exprimer vn
en fonction de n. En déduire que pn = 0,8 +0,2 x0,5n-1.
vn = 0,2 x 0,5n-1.
pn = vn +0,8 = 0,2 x 0,5n-1+0,8.
c. déterminer la
limite de la suite (pn).
0,5n-1 tend vers zéro si n tend vers l'infini.
pn tend vers 0,8 si n tend vers plus l'infini.
|
|