Mathématiques,
fonctions, QCM, Bac S Centres
étrangers 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Exercice 1 ( 4 points ).
On se propose de tester un prototype de hotte aspirante.
A l'instant t = 0, la hotte est mise en marche et fonctionne
pendant 20 minutes. Les mesures permettent de modéliser le taux de CO2 ( en %) contenu dans le local au bout de t minutes de fonctionnement de la hotte par la fonction f définie sur [0 ; 20 ] par :
f(t) =(0,8 t +0,2)e-0,5t +0,03.
On donne le tableau de variation de cette fonction.
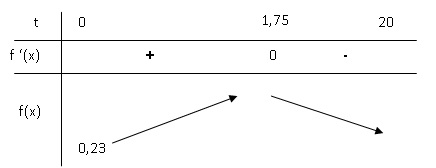
1.a. Calculer f(20).
f(20) = (0,8 x20 +0,2)e-10 +0,03 = 0,0307 ~0,031.
1.b. Déterminer le taux maximal de CO2 présent dans le local.
f(1,75) = (0,8 x1,75 +0,2) e-0,875 +0,03 = 0,697.
2. On souhaite que le taux de CO2 dans le local retrouve une valeur V < 3,5 %.
a. Justifier qu'il existe un unique instant T satisfaisant à cette condition.
f(0 ) = 0,23 ( 23 %) ; f(1,75) = 0,697 ( 69,7 %) ; sur [0 ; 1,75), f(t) est strictement croissante.
T n'appartient pas à cet intervalle.
f(1,75) = 0,697 ( 69,7 %) ; f(20) = 0,031 ( 3,1 %) ; sur [1,75 ; 20), f(t) est strictement décroissante.
T appartient à cet intervalle.
D'après le corollaire du théorème des valeurs intermédiaires, l'équation f(t) = 0,035 admet une unique solution sur [0 ; 20 ].
b. On considère l'algorithme suivant :
t <-- 1,75
p <--0,1
V <--0,7
Tant que V >0,035
t <-- t+p
V <-- (0,8t+0,2)e-0,5t+0,03
Fin Tant que
Quelle est la valeur de t à la fin de l'algorithme ? Que représente cette valeur dans ce contexte ?
La calculatrice donne f(15,65) =0,0351, supérieure à 0,035 et f(15,75) =0,03486, inférieur à 0,035.
L'algorithme donne t = 15,75 minutes ou 15 min 45 s.
Au bout de 15 min 45 s, le taux de CO2 est inférieur à 3,5 %.
3. On désigne par Vm le taux moyen de CO2 présent dans le local pendant les 11 premières minutes de fonctionnement de la hotte.
a. Soit F la fonction définie sur [0 ; 11 ) par F(t) = (-1,6 t -3,6)e-0,5t +0,03t.
Montrer que F est une primitive de f(t) sur [0 ; 11].
Dériver F en posant u = -1,6t-3,6 et v = e-0,5t ; u' = -1,6 ; v' = -0,5 e-0,5t.
u'v + v'u = -1,6 e-0,5t +0,5(1,6t+3,6)e-0,5t = (-0,8t +0,2)e-0,5t.
F ' = (-0,8t +0,2)e-0,5t +0,03 = f(t).
b. En déduire Vm.
F(11) = (-1,6 x11 -3,6)e-5,5 +0,03x11=0,2434 ; F(0) = -3,6.
Vm = (F(11)-F(0)) / 11 =(0,2434+3,6) / 11 = 0,3484 ( 34,9 %).
.
|
|
|
|
|
Exercice 2 ( 4 points).
1. Un type
d'oscilloscope a une durée de vie ( en années) qui peut être modélisée
par une variable aléatoire D qui suit la loi exponentielle de paramètre
l.
On sait que la durée de vie moyenne de ce type d'appareils est de 8 ans.
Affirmation 1.
Pour un oscilloscope de ce type choisi au hasard et ayant déja
fonctionné pendant 3 ans, la probabilité que la durée de vie soit
supérieure ou égale à 10 ans est égale à 0,42.
La loi exponentielle est à durée de vie sans vieillissement.
P3(D > 10) = P(D > 7) = e-7l avec l = 1 / 8 = 0,125 an-1.
P(D > 7) = e-0,875 ~0,42. Affirmation vraie.
2. En 2016, les forces de l'ordre ont réalisé 9,8 millions de dépistages d'alcoolémie et 3,1 % de ces dépistages étaient positifs.
Une brigade de gendarmerie a effectué 200 dépistages.
Affirmation 2 : la probabilité que, sur 200 dépistages, il y ait eu strictement plus de 5 dépistages positifs, est égale à 0,59.
On note X la variable aléatoire qui compte le nombre de dépistages positifs.
n = 200, répétition de n événements indépendants et identiques.
Chaque tirage conduit à deux issues possibles :
p = 0,031 dépistage positif e 1-p = 0,969, dépistage négatif.
La variable X suit une loi binomiale de paramètre n = 200 et p = 0,031.
P(X > 5) = 1 -P(X < 5) = 1-0,41 =0,59. Affirmation vraie.
|
|
3. On considère dans R l'équation : ln(6x-2)+ ln(2x-1) = ln(x).
Affirmation 3 : L'équation admet deux solutions dans l'intervalle ]0,5 ; +oo[.
ln(6x-2)+ ln(2x+1) = ln(x) est définie si : 6x-2 > 0 soit x > 1 / 3 ; 2x-1 >0 soit x > 0,5 ; x >0.
ln(6x-2)+ ln(2x+1) = ln(x) est définie dans l'intervalle ]0,5 ; +oo[.
ln((6x-2)(2x-1)) -ln(x) = 0 ;
ln((6x-2)(2x-1)=ln(x).
(6x-2)(2x-1) = x.
12x2-11x +2 =0.
D = (-11)2-4 x2x12 = 25.
Solutions : (11 +5) / 24 = 2 / 3 ; (11 -5) / 24 =1 / 4. Affirmation fausse.
4. On considère dans C l'équation : (4z2 -20z +37)(2z-7+2i)=0.
Affirmation 4. Les solutions de cette équation sont les affixes de points appartenant à un même cercle de centre le point P d'affixe 2.
4z2 -20z +37=0 ;
D = (-20)2 -4 x4x37 = -192 =192 i2.
Solutions : z1 = (20 +i 192½) / 8 =2,5 +i 3½ et z2 = (20 -i 192½) / 16 = 2,5-i 3½ .
2z-7+2i = 0 ; z3 = 3,5-i.
On note A, B et C les points d'affixes respectives z1, z2, z3.
PA = |z1-2| = |0,5 +i 3½ |= 13½ / 2.
PB = |z2-2| = |0,5 -i 3½ |= 13½ / 2.
PC = |z3-2| = |1,5 -i |= 13½ / 2. Affirmation vraie.
|
|