Le badminton,
un sport dans le vent, Bac S Centres étrangers 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Le
volant de masse m = 5,0 g est un projectile aux propriétés
aérodynamiques particulières qui lui donnent une trajectoie très
différente des balles utilisées dans les sports de raquettes. Les
plumes créent une traînée, modélisée par une force F, qui s'oppose au
mouvement du volant dans l'air. Le mouvement du volant est étudié dans
le référentiel terrestre supposé galiléen. Sur le graphe ci-dessous,
l'intervalle de temps entre 2 points de mesure vaut Dt = 50 ms.
1. Première approche.
1.1. Justifier le fait que le volant n'est pas en chute libre.
Un corps en chute libre n'est soumis qu'à son poids. Or le volant est soumis à son poids et à une force de traînée due à l'air.
1.2
Comment peut-on en première approximation décrire le mouvement du
volant sur la portion AB de sa trajectoire ? Représenter le vecteur
accélération ( direction et sens uniquement ) à la date t = 100 ms..
1.3.
Représenter sans souci d'échelle, les forces qui s'exercent sur le
volant en un point de AB. Les intensités de ces forces sont-elles du
même ordre de grandeur ? Justifier en utilisant la seconde loi de
Newton.
t(ms)
|
0
|
50
|
100
|
150
|
200
|
altitude y (m)
|
2
|
3.2
|
4.3
|
4.9
|
5.5
|
x (m)
|
0
|
1,15
|
2
|
2,7
|
3,2
|
Vitesse à la date t = 50 ms : calcul de la vitesse moyenne entre 0 et 100 ms.
vy 50 = Dy / Dt = (4,3-2) / 0,100 = 23 m /s.
vx 50 = Dx / Dt = 2 / 0,100 = 20 m /s.
Vitesse à la date t = 150 ms : calcul de la vitesse moyenne entre 100 et 200 ms.
vy 150 = Dy / Dt = (5,5-4,3) / 0,100 = 12 m /s.
vx 150 = Dx / Dt = (3,2-2) / 0,100 = 12 m /s.
Accélération à la date t = 100 ms :
ay = (12-23) / 0,1=110 m s-2.
ax = (12-20) / 0,1 = 80 m s-2.
a = (1102 +802)½ ~136 m s-2, très supérieure à g =9,8 m s-2.
Le poids est 13 fois plus faible que la somme vectotielle des forces (
poids et trainée). La trainée est très supérieure au poids.
Direction du vecteur accélération : celle de la variation du vecteur
vitesse. Le vecteur vitesse étant dirigé suivant AB, l'acélération est
dirigée suivant AB.
Sens du vecteur accélération : la vitesse diminue ; la variation du
vecteur vitesse est négative ; le sens du vecteur accélération est de B
vers A.
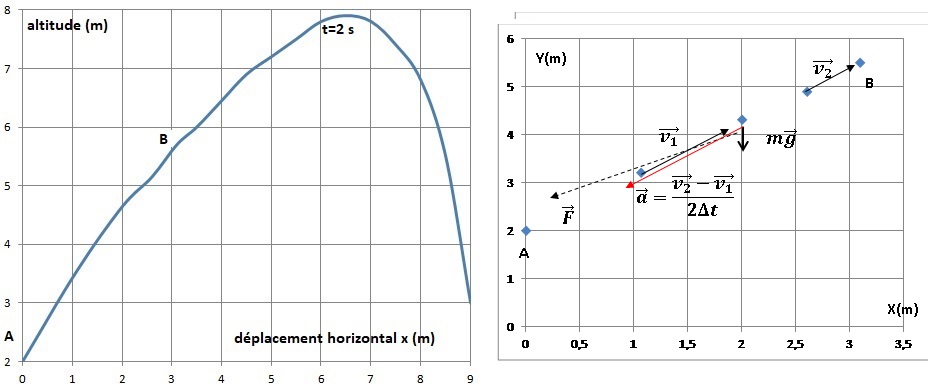
Entre A et B, le mouvement est rectiligne et ralenti..
|
|
.
.
|
|
2. Etude énergétique du mouvement.
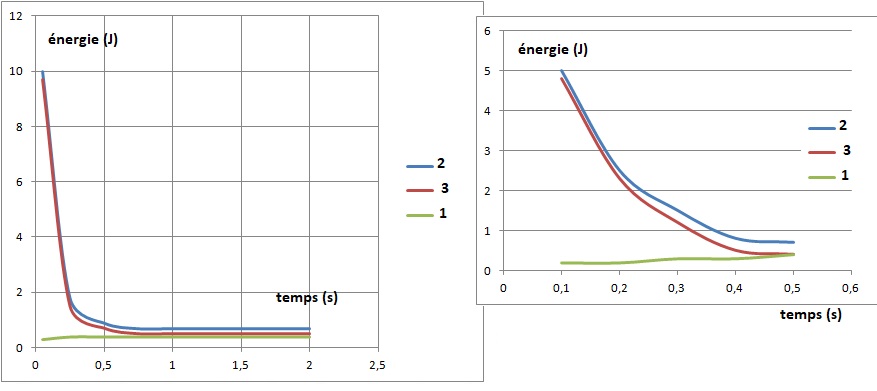
2.1 Identifier en justifiant, la nature de l'énergie correspondant à chaque courbe.
Courbe 1: l'énergie potentielle de pesanteur est initialement nulle, puis elle croît.
Courbe 2 : énergie mécanique, somme de l'énergie potentielle et de l'énergie cinétique.
Courbe 3. L'énergie cinétique et la vitesse sont maximales à t = 0 puis elles décroissent.
2.2. A partir de
l'une des courbes, calculer en km / h l'ordre de grandeur de la vitesse
du volant lorsqu'il occupe la position B ( date t = 0,2 s)
L'énergie cinétique est voisine de 2 J.
½m v2 = 2 ; v2 = 4 / m = 4 /(5 10-3) ~800 ; v ~28 m /s soit 28 x3,6 ~100 km /h.
2.3. Calculer le travail du poids lors du déplacement de A à B.
Le travail du poids est résistant en montée.
W = -mg(yB-yA) = -5 10-3 x 9,8 (5,5 -2) ~ -0,17 J.
2.4. L'énergie mécanique varie au cours du mouvement. Quelle en est la cause ?
L'énergie mécanique diminue du travail des frottements ( force de traînée ).
|
|
3. L'expérience de Thomas Pesquet.
Comment ce volant de badminton se comporte (til en apesanteur ?
A bord de la station ISS ( altitude de l'orbite h =400 km) les modules
sont pressurisés. La pression de l'air est égale à la pression
atmosphérique terrestre.
T. Pesquet lâche le volant sans vitesse initiale. Le volant rest près de l'astronaute.
3.1. Décrire le
mouvement du volant lorsqu'il est lâché par T. Pesquet dans le
référenteil lié à l'ISS puis dans le référentiel géocentrique.
Dans le référentiel lié à l'ISS, le volant est immobile.
Dans le référentiel géocentrique, l e volant est animé d'un mouvement circulaire uniforme.
3.2. Etablir l'expression de la valeur de l'accélération de l'ISS dans le référentiel géocentrique puis la calculer.
L'ISS est animée d'un mouvement circulaire uniforme. Elle n'est soumise
qu'à la force de gravitation centripète exercée par la terre.
La seconde loi de Newton conduit à : a = GMterre / (Rterre + h)2 =6,67 10-11 x5,97 1024 / ((6380 +400) 103)2 = 8,66 m s-2.
3.3. Expliquer pourquoi le volant reste près de l'astronaute.
Dans le référentiel de l'ISS le volant est pseudo-isolé.
De plus sa vitesse initiale est nulle. La première loi de Newton indique que le volant reste au repos.
|
|