Communication
sous-marine, Bac S Asie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Les sonars utilisent des ondes sonores dont l'étude en milieu aquatique est appelée acoustique sous marine.
1. Les débuts de l'acoustique sous marine.
En 1825 Charles Sturm détermine la vitesse des ondes sonores dans l'eau du lac Léman selon le protocole suivant :
Un premier expérimentateur produit un son dans l'eau et dans le même temps il lance une fusée.
Depuis un second bateau situé à environ 1000 m du premier, un second
expérimentateur plonge la tête dans l'eau et indique par un signe du
bras la réception du bruit à un troisième expérimentateur en charge du
chronomètre. Le chronomètre indique les quarts de seconde. Les valeurs
de la vitesse du son dans l'eau étaient trop approximatives.
En 1826 le protocole est amémioré.
Bateau émetteur : une cloche immergée est frappée et en même temps un
disposiitif enflamme une poudre formant un signal lumineux observable
par le second expérimentateur présent dans le bateau récepteur.
Bateau récepteur : le son est perçu grâce à un long tube cylindrique à
l'extrémité duquel il applique l'oreille. Le chronomètre est le même.
1.1. Lors de l'expérience de 1825, pourquoi l'expérimentateur lance -t-il une fusée ?
Dès que le troisième expérimentateur aperçoit la lumière de la fusée, il déclenche son chronomètre.
1.2. Identifier au moins deux sources d'erreurs sur la valeur de la mesure de la vitesse du son.
La fusée est allumée avec un petit retard par rapport à l'émission sonore.
La fusée doit s'élever assez haut pour être vue par le bateau récepteur.
Il existe un faible intervalle de temps entre la réception du signal sonore et le mouvement du bras.
La distance des deux bateaux n'est pas connue avec précision.
1.3 Quelles améliorations sont-elles apportées par le second protocole en 1826 ?
Le chronométreur n'a pas besoin d'un troisième expérimentateur.
La distance des bateaux est plus précise ( moins de 20 m).
1.4. Le son met 9,4 s pour parvenir au bateau récepteur ; distance des deux bateaux : 13 487 m
L'incertitude relative sur la valeur de la vitesse v s'écrit :
U(v) / v = [(U(d) / d)2 + U(Dt) / Dt)2]½.
Donner un encadrement de la valeur de la vitesse du son dans l'eau.
v = 13487 / 9,4 = 1,435 103 m /s.
U(v) / v = [(20) / 13487)2 + U(0,25) /9,4)2]½=0,0266 ; U(v) = 0,0266 x 1,43 103 ~38 m /s..
v est compris entre 1397 m/s et 1473 m /s.
1.5. Dans une note en bas de page J D Colladon signale que "l'erreur possible danns cette expérience ne peut pas s'élever au 1 / 60è de la valeur véritable". Cette affirmation est-elle cohérente avec le résultat précédent ? Justifier.
1435 / 60 ~24 m/s.
L'incertitude relative est supérieure à 1 / 60è. L'affirmation n'est pas cohérente avec le résultat.
|
|
...
|
|
2. Impact de l'utilisation des sonars sur la faune sous-marine.
En 2008 un échouage de dauphins est provoqué par un navire faisant des relevés topographiques à 65 km du lieu de l'échouage.
A 1 m de l'émetteur d'un sonar, le niveau d'intensité sonore maximal peut atteindre 240 dB.
On modèlise le signal sonore émis par un sonar par une fonction sinusoïdale du temps.
2.1. Vériifier que la fréquence d'émission est f=12 kHz.
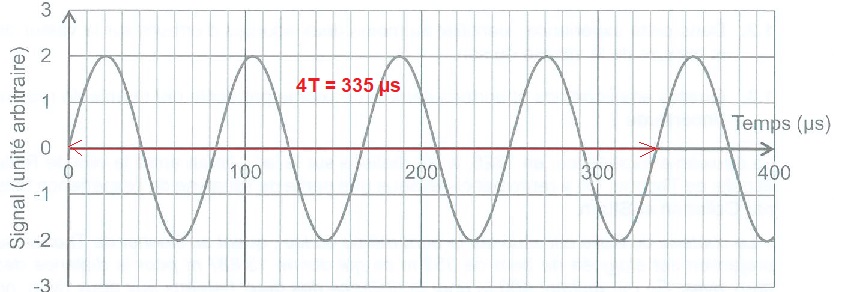
T = 335 / 4 ~84 µs ; f = 1 /(84 10-6) = 11904 Hz ~12 kHz.
2.2. Ce signal appartient-il au domaine audible des êtres humains ?
L'oreille humaine perçoit les sons dont les fréquences sont
comprises entre 20 Hz et 20 kHz. Un son de fréquence 12 kHz est donc
audible.
Phénomène d'atténuation des ondes sonores.
L'intensité sonore I reçue en un point M, situé à la distance R de la
source acoustique S, est liée à la puissance acoustique P de la source
par : I = P / (4pR2).
2.3.a. On considère que dans l'eau le seuil d'audibilité est I0 = 7,00 10-17 W m-2. En déduire la valeur de l'intensité sonore maximale à 1 m du sonar.
I = I0 x 1024 = 7,00 10-17 x 1024 = 7,00 107 W m-2.
2.3.b. Montrer que la puissance de la source est 8,80 108 W.
P =4pR2I = 4 x3,14 x12 x7,00 107 = 8,80 108 W.
2.3.c. En déduire que le niveau d'intensité sonore à 65 km du sonar vaut environ 144 dB.
I = 8,80 108 /(4 x3,14 x(6,5 104)2) = 1,66 10-2 W m-2.
L =10 log (I / I0) = 10 log ( 1,66 10-2 / (7,00 10-17)) = 143,7 ~144 dB.
|
|
Le
milieu de propagation absorbe une partie de l'énergie de l'onde sonore.
le niveau d'intensité sonore subit une perte supplémentaire en
décibel égale à aR où a
est un coefficient d'absorption qui dépend de la fréquence de
l'onde, et où R est la distance entre la source et le récepteur.
2.3.d. Estimer la
valeur de la diminution du niveau d'intensité sonore en dB dans la situation étudiée.
Pour une fréquence de 12 kHz, a ~ 1 dB / km.
Diminution d u niveau d'intensité sonore : 65 dB.
2.4. La courbe ci-dessous indique le niveau sonore minimal pour qu'un son de fréquence f soit audible par un dauphin.
Les dauphins ont-ils pu percevoir l'émission du sonar du navire ?
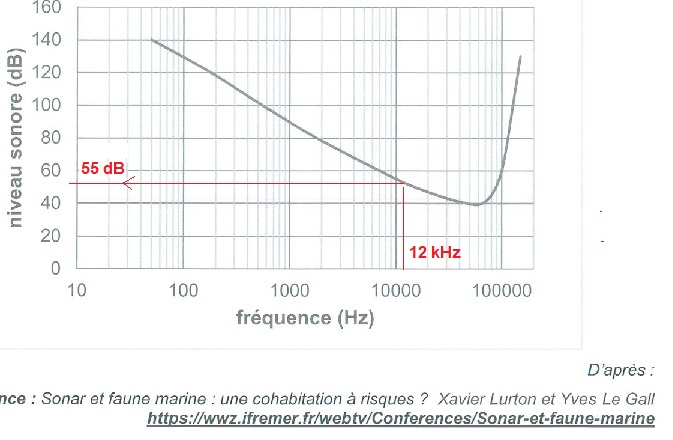
144 -65 = 79 dB, valeur supérieure au niveau sonore minimal ( 55 dB). Le signal du sonar a donc pu être perçu par les dauphins.
|
|