Etude du vol
d'une balle de golf, Bac S Asie 2018
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
Le
swing d'un joueur de golf permet d'envoyer la balle à une distance
appelée portée d'environ 250 m, distance mesurée horizontalement.
1.Vitesse initiale de la balle.
Le schéma qui suit propose la reconstitution d'une chronophotographie
du mouvement d'une balle de golf après sa propulsion par un club. La
caméra permet d'enregistrer 1000 images par seconde. La figure montre
les 9 premières images de l'enregistrement de la balle, la première
image correspond à la position initiale. Le golfeur représennté n'est
pas à l'échelle.
1.1. Déterminer l'intervalle de temps qui séppare deux images.
1 / 1000 = 10-3 s = 1 ms.
1.2 A quel mouvement simple peut être assimilé le mouvement de la balle au début du vol ?
Les distances parcourues durant des durées égales sont égales. le mouvement est rectiligne uniforme.
1.3. Déterminer la vitesse initiale V0.
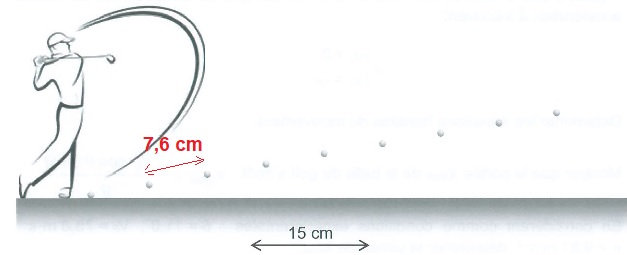
7,6 10-2 / 10-3 = 76 m /s.
2. Mouvement de la balle modèlisée par un point matériel de masse m = 46 g.
Dans ce modèle la résistance de l'air n'est pas à prendre en compte. A la date t = 0, la balle est à l'origine du repère.
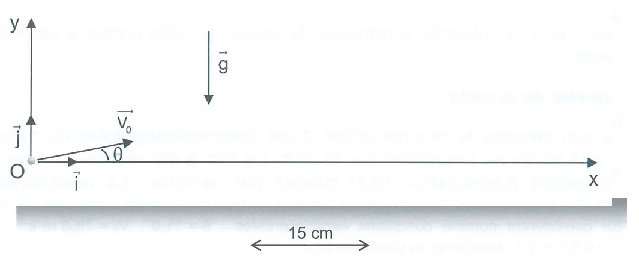
2.1. Montrer que les composantes du vecteur 'accélération s'écrivent : ax = 0 et ay = -g.
La balle en chute libtre n'est soumise qu'à son poids, verticale, vers le bas, valeur mg.
La seconde loi de Newton conduit à : ax = 0 et ay = -g.
2.2. Déterminer les équations horaires du mouvement.
Le vecteur vitesse est une primitive du vecteur accélération.
Composantes du vecteur vitesse initiale : V0 cos q ; V0 sin q.
vx = V0 cos q ; vy = -gt +V0 sin q.
Le vecteur position est une primitive du vecteur vitesse.
La position initiale est l'origine du repère.
x = V0 cos q t : y = -½gt2 + V0 sin q t.
2.3. Montrer que la portée s'écrit xmax = 2 V02 cos q sin q / g.
t = xmax / V0 cos q ; repport dans y :
0 = -½g(xmax / (V0 cos q ))2 +V0 sin q xmax / (V0 cos q ) ;
0 = -½g xmax / V02 cos q + sin q ;
xmax = 2 V02 cos q sin q / g.
2.4. A.N . q = 11,0° : V0 = 75,0 m /s ; g = 9,81 m s-2.
xmax = 2 x75,02 cos 11 x sin 11 / 9,81 ~215 m.
2.5. Comparer cette
valeur avec celle de l'énoncé, et indiquer en quoi la valeur réelle de
la portée dans l'air peut sembler surprenante.
La
valeur calculée est inférieure d'environ 14 % par rapport à la
valeur réelle. Il faut prendre en compte les frottements.
|
|
...
|
|
3. De l'importance de l'air dans le vol d'une balle de golf.
La balle n'est plus modèlisée par un point matériel.
Lorsque le golfeur frappe la balle, il utilise un club qui la propulse
avec un angle d'une dizaine de degrés par rapport au sol.
l'impact du club avec la balle a également pour conséquence de mettre
celle-ci en rotation sur elle-même. Ces rotations peuvent atteindre la
fréquence de 2700 tours par minute.
L'effet Magnus se manifeste lorsque la balle possède un mouvement de rotation dans l'air.
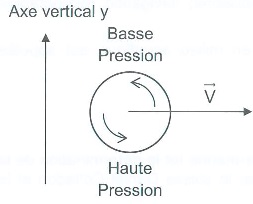
L'air qui passe au dessus de la balle est entraîné par la rotation de celle-ci, sa vitesse augmente et sa pression diminue.
Inversement l'air qui passe au dessous de la balle serra sa vitesse diminuer et sa pression augmenter.
Cette différence de pression est à l'origine d'une force supplémentaire
F, verticale, vers le haut, supposée appliquée au centre de la balle et
constante, tout au long du mouvement. On néglige les autres effets dus
à l'air.
3.1. Représenter les forces modélisant les actions mécaniques s'exerçant sur la balle.
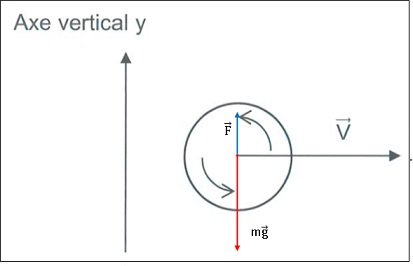
|
|
3.2. En déduire la nouvelle composante ay de l'accélération.
ay = -g + F / m.
3.3. Estimer la valeur de F pour retrouver la portée effectivement observée.
Dans l'expression de la portée, on remplace g par g-F / m.
xmax = 2 V02 cos q sin q / (g-F / m) ;
g-F / m = 2 V02 cos q sin q / xmax ;
F =m (g- 2 V02 cos q sin q / xmax ).
F = 46 10-3 ( 9,81-2x75,02 xcos11 xsin 11 /250) ~ 6,3 10-2 N.
|
|