Lanceur de flipper, bac S Antilles 09 / 2018

Lanceur de flipper, Bac S Antilles 09 / 2018 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
	. .
	Exercice 2. (6 points) Au début de la partie, le joueur actionne une poignée qui comprime un ressort et permet de propulser la bille dans la rampe de lancement. On souhaite déterminer si le ressort vendu sur un site marchand pourra être utilisé pour remplacer un ressort défectueux du lance-bille du flipper. Caractéristiques du ressort vendu : raideur 33 N m^-1 ; écrasement maximal Dl = 90 mm. Détermination expérimentale de la raideur d'un ressort.. La masse du ressort est supposée négligeable devant celle de la masse marquée, notée m ; le référentiel est celui du laboratoire et le système est la masse marquée de centre G ; on néglige les frottements ; la position de G est repérée par son abscisse x(t). Le ressort est suspendu verticalement par une de ses extrémités fixe. La masse marquée est fixée à son extrémité libre puis mise en mouvement verticalement. 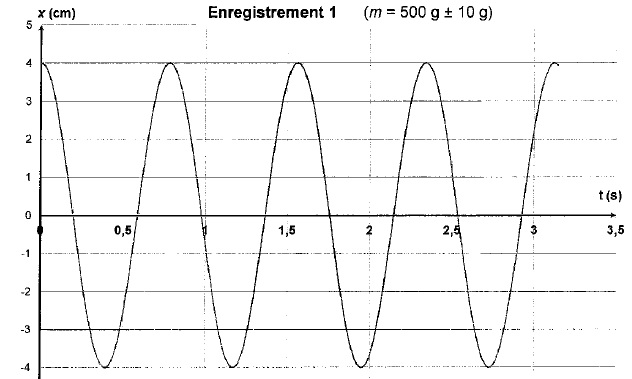Un capteur de position relié à un système d'acquisition informatisé permet d'enregistrer les variations de la position de G en fonction du temps. Trois expériences sont réalisées :
	...
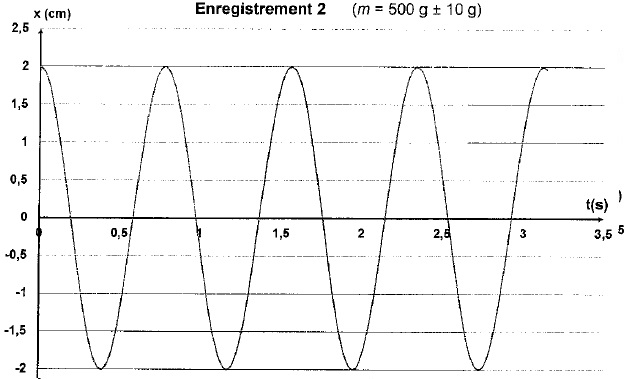
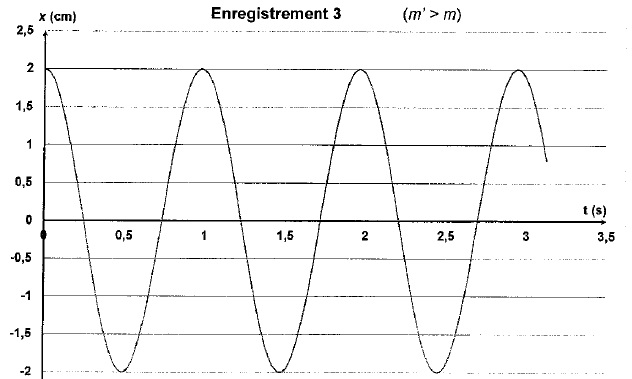
	1.1. En comparant les enregistrements 1 et 2, identifier la modification effectuée. La masse reste inchangée ; l'amplitude initiale est divisée par 2 ( enregistrement 2). 1.2. L'amplitude de G a -t-elle une influence sur la période ? Justifier. Non. La période sur l'enregistrement1 est identique à celle de l'enregistrement 2. 1.3 Que peut-on dire de l'influence de la masse sur la période des oscillations ? Enregistrement 3 : quand la masse augmente, la période des oscillations croît. 1.4. Influence de la constante de raideur du ressort. 1.4.1. Ces trois enregistrements permettent-il d'affirmer que la consatnte de raideur k du ressort a une influence sur la période des oscillations ? Justifier. Non. Aucune indication concernant la raideur du ressort n'est mentionnée. 1.4.2. Proposer une expérience supplémentaire permettant de conclure sur ce point. Faire un enregistrement avec un ressort de raideur différente en conservant la même masse m. 1.5.On propose trois expressions pour la période T₀ des oscillations. 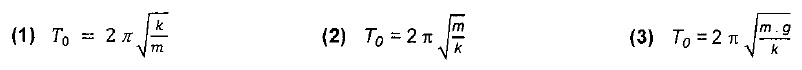1.5.1. Montrer que l'expression 1 ne convient pas. La période et la masse varient dans le même sens. La masse doit figurer au numérateur. 1.5.2. Par analyse dimensionnelle montrer que l'expression 3 ne convient pas. mg a la dimension d'une force ( newton N) ; k s'exprime en N m^-1 ; mg / k s'exprime en m ; 2p est sans dimension et T₀ s'exprime en seconde.
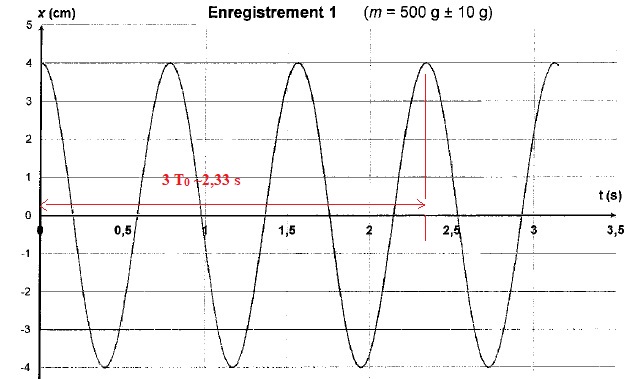
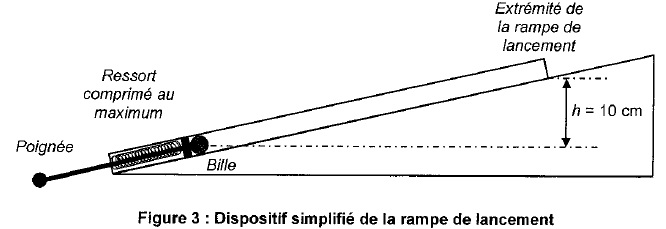
	1.6. On admet que T₀ = 2p ( m /k)^½. Déterminer T₀ ( enregistrement 1). T₀ = 0,775 s. 1.7. Les caractéristiques fournies pour le ressort du site marchand sont-elles validées ? k = (4p²m) / T₀² = (4 x3,14² x0,500) / 0,775² =32,8 N m^-1. La raideur est validée. Evaluation des performances du ressort. On souhaite s'assurer que le ressort proposé permette à la bille d'atteindre l'extrémité de la rampe de lancement pour déboucher dans le plateau de jeu. Masse de la bille m = 100 g ; g = 9,81 m s^-2 ; hauteur de la rampe h = 10 cm. En réalisant un raisonnement énergétique simple ( en négligeant toute perte d'énergie), montrer que l'énergie élastique emmagasinée par le ressort est suffisante pour permettre à la bille d'atteindre l'extrémité de la rampe. Calculer la vitesse de la bille à l'extrémité de cette rampe. Energie potentielle élastique initiale : ½k Dl² = 0,5 x 33 x0,09² = 0,13365 J. Energie potentielle de pesanteur finale : mgh = 0,100 x9,81 x0,10 = 0,0981 J. L'énergie mécanique finale de la bille est sous forme potentielle de pesanteur et cinétique. ½mv²=0,13365 -0,0981 = 0,03555 J. L'énergie cinétique de la bille n'est pas nulle au sommet de la rampe. La bille atteint donc le sommet avec une vitesse : v = (2 x0,03555 / 0,100)^½ ~0,843 m s^-1.