Mathématiques,
concours Aspts Lille
2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
1. Développer et réduire :
A = -(3x+2)(3x-2) +(9x-10)2.
A = -(9x2-4)+81x2+100-180x.
A =72x2-180x+104.
B =(x+9)2 -(8x+3)(-9x-6).
B = x2+81+18x+(8x+3)(9x+6).
B = x2+81+18x+72x2+48x+27x+18.
B = 73x2+93x+99.
2. Calculer les expressions suivantes et donner le résultat sous la forme a racine carrée de b avec a et b mes entiers les plus petits possibles.
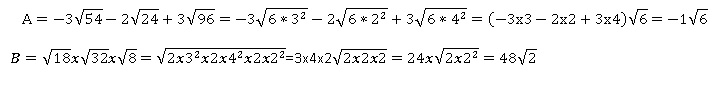
3. A =(10x-1)(4x-9)+(4x-9)2.
Réduire et ordonner A.A=40x2-90x-4x+9+16x2+81-72x
A =56x2-166x+90.
Factoriser A.
A = (4x-9)[10x-1+4x-9]
A = (4x-9)(14x-10).
Calculer A pour x = -1 / 9.
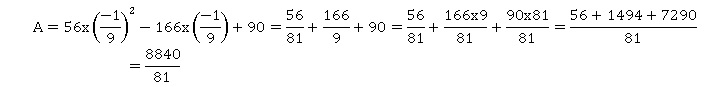
Résoudre l'équation A = 0.
Pour qu'un produit de facteurs soit nul, il suffit que l'un des facteurs soit nul.
4x-9 =0 ; 4x = 9 ; x = 9 / 4.
14x-10=0 ; 14 x = 10 ; x = 10 / 14 ; x = 5 / 7.
4.
d1 est représentative de la fonction h.
4.1. Donner l'image de -1,5 par la fonction h. 1.
4.2. Donner un nombre qui a pour image 2,5 par la fonction h. 1.
4.3. Tracer la droite (d2) représentative de la fonction k : y = -1,5 x-4.
Cette droite passe par le point (0 ; -4) et par le point ( -2 ; -1).
4.4. Déterminer l'expression de la fonction représentée par la droite d1.
Fonction affine décroissante de pente ( coefficient directeur ) -1.De plus elle passe par le point (0 ; 4). y = -x +4.
|
|
|
5.
Un jeune berger se trouve au bord d'un puits cylindrique de diamètre
intérieur 70 cm. Il aligne son regard vers le bord inférieur du puits
et le fond pour en estimer la profondeur.
BC = 0,20 m ; BH= 1 m ; RH = 1,8 m.
5.1. Donner les longueurs FG et RB.
RB = 1,8 -1 = 0,8 m.
FG = 0,7 +0,2 = 0,90 m.
5.2.Calculer la profondeur BG.
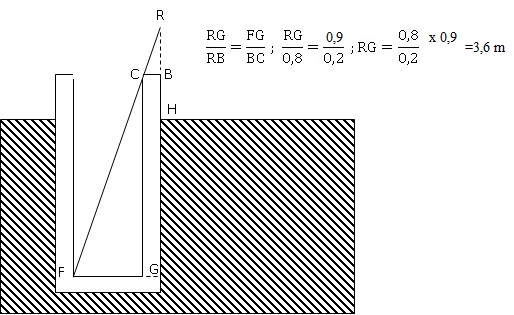
BG = RG -RB = 3,6-0,8 = 2,8 m.
5.3. La hauteur d'eau dans le puits est 2,60 m.. Il a besoin de 1 m3 d'eau pour abreuver ses moutons.
En trouvera t-il assez dans ce puits ?
Volume d'un cylindre : V = p r2 h =3,14 x0,352 x2,6 ~1,0 m3. Donc il y a assez d'eau.
6..
Notes d'un devoir commun pour les élèves de troisième.
note
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
effectif
|
0
|
0
|
2
|
2
|
2
|
3
|
5
|
3
|
5
|
5
|
10
|
6
|
5
|
7
|
5
|
4
|
4
|
2
|
1
|
1
|
0
|
fréquence
|
0
|
0
|
0,027
|
|
0,068
|
0,041
|
0,068
|
0,14
|
0,081
|
0,068
|
0,095
|
0,068
|
0,054
|
0,027
|
0,014
|
0
|
fréquence = effectif / total ( 72).
6.2. Combien d'élève ont-ils obtenu une note strictement supérieure à 10 ? 35.
6.3. Quel est le pourcentage d'élèves ayant obtenu au plus 7 ?
15 élèves ont obtenu une note inférieure ou égale à 7.
17 / 72 x100 =23,6 ~24 %
6.4. Calculer la médiane de ces notes. 10
6.5. Un élève est dit moyen s'il obtient les notes 9; 10 ; 11. Quel est le pourcentage d'élève moyen ?
21 / 72 x100 ~29 %.
|
|