Dualité onde
corpuscule, les exoplanètes, détection d'un tsunami.
Concours Orthoptie Nantes 2017.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Dualité onde corpuscule. ( 7
points)..
A. Le comportement
ondulatoire de l'électron.
En 1923, Louis de Broglie propose d'associer une onde à une particule
matérielle comme l'électron.
Dans
l'expérience de Davisson et Germer, un faisceau d'électrons
monocinétiques est envoyé sur un cristal de nickel. Après réflexion sur
le cristal, le faisceau est recueilli sur une plaque fluorescente et
des taches de diffraction sont observées.
La figure de diffraction est identique lorsqu'un même cristal diffracte
des rayons X ou des électrons dont la longueur d'onde calculée par la
relation de Louis de Broglie est égale à celle des rayons X.
L'expérience de Thomson est basée sur le même principe : une très mince
feuille métallique est frappée par un faisceau d'électrons
monocinétiques. L'étude ne porte plus sur les électrons réfléchis mais
sur les électrons transmis au travers de la feuille. La figure de
diffraction obtenue constituée de cercles concentriques est analogue à
celle obtenue avec des rayons X.
1.a. Sur quel phénomène physique sont
basées les deux expériences ? En quoi diffèrent -elles ?
La
diffraction est observée lorsqu'une onde rencontre un obstacle ou un
trou dont les dimensions sont du même ordre de grandeur que la longueur
d'onde de l'onde.
Expérience de
Davisson et Germer
: un cristal se comporte comme un réseau. Les atomes sont alignés
régulièrement dans la structure cristalline. Chaque atome diffracte le
faisceau d'électrons ( ou les rayons X) incidents ; un pic d'intensité
est observé dans les directions où les différentes ondes diffractées
interfèrent constructivement.
Expérience de
Thomson : une feuille métallique remplace le cristal de nickel.
1.b. Pourquoi
constituent-elles une preuve expérimentale de l'hypothèse de Louis de
Broglie ?
La
diffraction est un phénomène caractéristique d'une onde.
2.a.
Un cristal est formé d'un empilement d'atomes bien prganisés, formant
ainsi des plans atomiques. dans les cristaux, les distances entre les
plans sont de l'ordre de 10-10 m.
Justifier l'utilisation de rayons X de l'ongueur d'onde comprise entre
10-11 et 10-9 m pour les études de
cristallographie par diffraction.
La longueur d'onde des rayons X doit être du même ordre de grandeur que
la distance entre deux plans pour obtenir une figure de diffraction.
2.b.
Rappeler la relation de Louis de Broglie donnant la longueur d'onde
associée à un électron. Préciser le nom des grandeurs et leurs unités.
l = h
/ p.
l :
longueur d'onde en mètre ; h : constante de Planck ( J s) ; p :
quantité de mouvement en kg m s-1.
2.c.
Calculer la longueur d'onde associée à des électrons d'énergie
cinétique 100 eV. Dans l'hypothèse d'un comportement ondulatoire,
peuvent-ils être diffractés par un cristal ?
Ec = p2 / (2m)
; p = (2mEc)½ avec Ec = 100 x1,6 10-19
=1,6 10-17 J.
p = (2x9,1 10-31 x1,6 10-17)½ =5,4 10-24
kg m s-1.
l =
6,63 10-34 / (5,4 10-24) ~1,2 10-10 m.
La longueur
d'onde des électrons est du même ordre de grandeur que la distance
entre deux plans atomiques : la diffraction se produira.
L'effet Compton
Compton envoie un faisceau de rayons X sur une cible
( mince feuille de graphite).
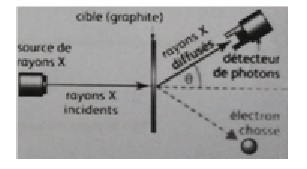
Il observe les phénomènes suivants :
Des électrons sont chassés de la cible en graphite.
Des rayons X sont diffusés dans toutes les directions.
La longueur d'onde l' des rayons X diffusés est plus grande que
la longueur d'onde l des rayons X incidents.
l' -l = 2,42 10-12
(1-cos q).
l'augmentation de la longueur d'onde des rayons X diffusés par les
électrons porte le nom d'effet Compton.
Interprétation
: la situation est celle d'un choc entre deux particules formant un
système considéré comme isolé : un photon d'énergie hn
et de quantité de mouvement p, avec un électron qui peut être considéré
comme libre et immobile dans les conditions de l'expérience.
La conservation de la quantité de mouvement et de l'énergie totale
conduit à :
l'
-l =h (1-cos q) / (me-c).
1.a A l'aide de la
phrase en gras, comparer les énergies des rayons X incidents et
diffusés.
E = hc /l.
Plus la longueur d'onde est grande, plus l'énergie est faible.
Les rayons X diffusés ont une énergie inférieure à celle des rayons X
incidents.
Lorsqu'un
photon X passe à proximité d'un électron périphérique peu lié à
l'atome, l'énergie du photon est en partie transmise à l'électron : ce
dernier est arraché de l'atome et s'échappe avec une certaine énergie
cinétique. Le reste de l'énergie se retrouve sous la forme d'un photon
X de direction différente et d'énergie inférieure.
1.b. Montrer que
l'expression h / (me-c),
appelée longueur d'onde de Compton, a la dimension d'une longueur.
Calculer sa valeur et la comparer à la valeur du résultat expérimental
donné.
h s'exprime en J s ; une énergie ( J) est une force ( N) fois un
déplacement (m) ; une force est uneh / (me-c) masse (kg) fois une accélération ( m s-2).
h s'exprime en kg m2 s-1.
me-c s'exprime en kg m s-1
; par suite h / (me-c) s'exprime en mètre.
h / (me-c) = 6,63 10-34
/(9,1 10-31 x3 108) = 2,43 10-12 m,
valeur identique à celle proposée.
1.c. En quoi, cette expérience
constitue-t-elle une preuve de l'aspect particulaire de la lummière ?
La lumière peut se comporter comme un faisceau de particules dont
l'énergie est proportionnelle à la fréquence.
2. Quantité de mouvement
et effet Compton.
La longueur d'onde des photons diffusés est de
71,0 10-12 m pour un angle q = 90°.
2.a Calculer la
longueur d'onde des photons incidents.
l'
-l = 2,42 10-12
(1-cos q)= 2,42 10-12
(1-cos90) = 2,42 10-12.
l = l' - 2,42 10-12
= (71,0-2,42) 10-12 = 68,58 10-12 m.
2.b. Calculer la
valeur p de la quantité de mouvement d'un photon incident et celle p'
d'un photon diffusé.
p =h / l = 6,63 10-34
/ (68,58 10-12)=9,67 10-24 kg m s-1.
p' =h / l
'= 6,63 10-34 / 71,0 10-12)=9,34 10-24
kg m s-1.
2.c. Réaliser un
schéma indiquant les vecteurs quantités de mouvement du rayon X
incident, du rayon X diffusé et de l'électron chassé dans le cas où q = 90°.
2.d.
Ecrire la relation traduisant la conservation de la quantité de
mouvement du système {photon électron } avant la collision et après la
collision.
2.e. En déduire la
valeur de la quantité de mouvement pe de l'électron.
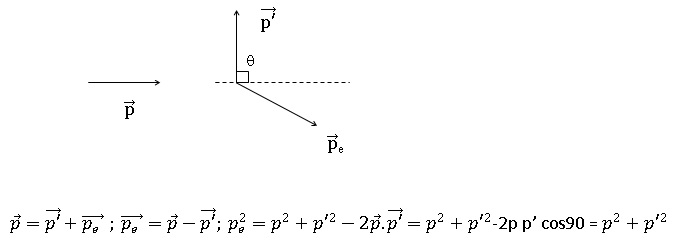
pe =( 9,672+9,342)½
10-24 =13,4 10-24 kg m s-1.
|
|
|
Exercice2 : les exoplanètes. 13,5
points
Les exoplanètes ont
été détectées indirectement par effet Doppler-Fizeau qu'elle engendrent
sur le spectre de leur étoile.
L'exoplanète
et son étoile tourne autour du barycentre de leur masse. ce mouvement
de l'étoile par rapport à l'observateur sur terre engendre un effet
Doppler sur la lumière de l'étoile.
Quand l'étoile avance vers la terre, son spectre est décalé vers les
hautes fréquences.
Quand l'étoile s'éloigne vers la terre,
son spectre est décalé vers les basses fréquences.
A partir de ce décalage des raies du spectre, on peut calculer la
vitesse de l'étoile par rapport à la terre. Ainsi, pour une étoile sans
planète, on observe une vitesse radiale constante. De plus, si cette
vitesse est négative, l'étoile se rapproche de l'observateur.
En utilisant cette méthode, on a établi ci-dessous la courbe donnant la
vitesse de l'étoile 51Pegasi par rapport à la terre sur une
cinquantaine de jours.
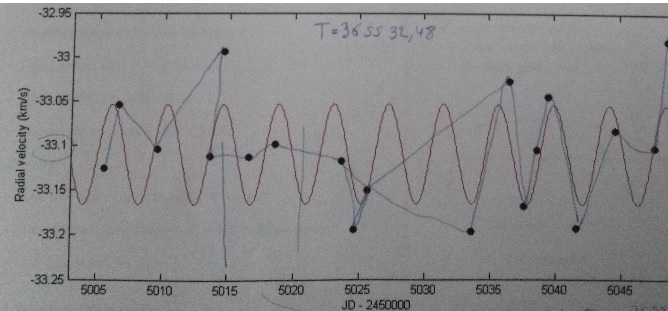
1. L'étoile 51Pegasi.
1.a. Comment
peut-on justifier qu'une exoplanète est présente autour de cette étoile
?
La vitesse radiale de cette étoile n'est pas constante.
1.b
Déterminer graphiquement la vitesse moyenne v de l'étoile 51Pegasi par
rapport à la terre.
v = -33,1 km /s.
1.c. Cette étoile
se rapproche ou s'éloigne-t-elle de la terre ? Justifier.
La vitesse moyenne de l'étoile étant négative, l'étoile se rapproche de
la terre.
1.d.
Comment nomme-t-on alors le décalage en fréquence des raies observées
dans le spectre de cette étoile ?
Décalage vers les hautes
fréquences, blueshift
1.e. Le
décalage spectral z des raies d'une source lumineuse en mouvement se
calcule avec les relations :
z = v / c ou z = (l-lref) / l.
Déterminer la valeur de la longueur d'onde l observée dans le spectre
de 51peg de vitesse radiale v = -33,110 km /s pour la raie D1
du sodium lref
= 588,9950 nm. On prendra c = 299 792,458 km /s.
z = -33,110 / 299 792,458 = -1,10443 10-4.
-1,10443 10-4 l
= l-588,9950 10-9.
l = 588,9950 10-9 / (1+1,10443
10-4) =5,88930 10-7 m = 588,930 nm.
|
|
|
|
2. L'exoplanète 51Pegb.
Sa masse m vaut 9,0 1026 kg ; elle est située à environ 50
années-lumière de la terre en orbite à une distance R du centre de son
étoile 51Pegasi de masse M.
Caractéristiques de l'orbite de 51Pegb :
Demi-grand axe de lellipse A = 0,053 u.a ; excentricité e = d /A = 0,01
; période de révolution T = 4,2307 j.
3è loi de Kepler T2 /R3 = 4p2 /(GM).
2.a. Comment se nomme la grandeur G ?
Constante de gravitation universelle.
2.b Où peut-on placer l'étoile
51Pegasi si l'ellipse représente l'orbite de l'exoplanète ?
L'étoile se trouve à l'un des foyers de l'ellipse.
2.c. Sachant
qu'un cercle est une ellipse dant les foyers sont confondus avec le
centre C, montrer à partir des caractéristiques de l'orbite que
l'exoplanète 51Pegb possède une trajectoire quasi-circiulaire.
L'excentricité vaut 0,01, valeur très faible ; l'orbite de l'exoplanète
est quasi-circulaire.
2.d. Montrer à
l'aide de la deuxième loi de Newton que le mouvement de cette planète
est uniforme.
Référentiel :
l'étoile centrale.
L'exoplanète est
soumise à la seule force de gravitation centripète exercée par l'étoile
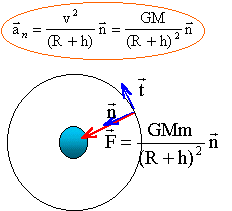
M : masse (kg) de l'étoile ; m : masse de l'exoplanète
(kg) ; R (m) rayon étoile ; h (m) altitude depuis le sol
suivant l'axe n la
seconde loi de Newton s'écrit : GMm /(R+h)² = m aN= mv²/
(R+h)
d'où la valeur de la vitesse (m/s): v² =GM / (R+h). indépendante de
la masse du satellite
la force de gravitation étant perpendiculaire à la
vitesse à chaque instant, ne travaille pas et en conséquence ne modifie
pas l'énergie cinétique de la planète. La valeur de la vitesse reste donc
constante : mouvement uniforme.
2.e. En utilisant
la courbe ci-dessus, retrouver en détaillant les calculs la période de
révolution T de 51Pegb dans l'unité SI.
10 T correspondent à 25 cm etv40 jours correspondent à 23,6 cm.
T = 25 /23.6 x4=.4,237 jours.
T=4,237 x24 x3600 =3,66 105 s.
2.f. Lors de la découverte de la
planète 51Pegb, la masse de son étoile 51Peg était déja connue.
M = 2,1 1030 kg. Déterminer le rayon R de l'orbite de 51Pegb.
4p2 /
(MG) = 4 x3,142 / (2,1 1030 x6,67 10-11)
= 2,818 10-19.
T2 /R3 = 2,818 10-19.
R3 = (3,66 105)2 / (2,818 10-19)=4,75
1029 ; R = 7,80 109 m.
2.g. Retrouver
l'expression littérale de la vitesse orbitale v de 51Pegb en fonction
de G, M et R. Déterminer sa valeur avec R = 8,0 109 m.
v = (GM/ R)½
=(6,67 10-11 x 2,1 1030 / (8,0 109))½=1,32
105 m /s.
3. Les exoplanètes 51Pegc et 51Pegd.
. 51 pegasi est une étoile de type naine jaune
quasi-identique à notre soleil bien que plus vieille de plus de 2
milliards d'années.
3.a. En supposant que les
trois exoplanètes en orbite autour de 51Peg ont une trajectoire
circulaire, montrer que v2R = constante.
v2 = GM / R , pour une étoile donnée GM est constant. Par
suite v2R est constant.
3.b. Que peut-on
déduire pour la vitesse orbitale vc de 51Pegc par rapport à
celle vb de 51Pegb sachant que 51Pegc est située plus loin
de son étoile que 51Pegb ?
vc2 Rc = vb2
Rb ; vc Rc
= vb (Rb
/ Rc )½
avec (Rb / Rc )
<1. Donc vc < vb.
3.c. Déterminer la
période Td de révolution de 51Pegd.
On donne : pour 51Pegc : demi-grand axe Ac = 25 ±2 u.a ;
période sidérale Tc =122 ±1 ans.
pour 51Pegd :
demi-grand axe Ad = 70 ±5 u.a.
T2 / A3
= constante.
Td = Tc (Ad / Ac)1,5
=122 ( 70 / 25)1,5 = 571 ans.
3.d déterminer un encadrement de la
valeur réelle de cette période.
On donne U(Td) = Td / 1,414 x[2(U(Tc)
/ Tc)2+3(U(Ac) / Ac)3+3(U(Ad)
/ Ad)3]½.
U(Td) = 571 / 1,414 x[2(1 / 122)2+3(2
/ 25)3+3(5 / 70)3]½~21ans.
Td = 571 ±21 ans . 550 < Td < 592 ans.
|
|
|
|
Exercice 3. Détection d'un tsunami.
3,5 points.
Un
tsunami est une vague géante ou une série de vagues, venant du fond de
l'océan. Il peut être provoqué par un séisme : celui-ci provoque le
soulèvement ou l'effondrement d'une partie du fond océanique, la masse
d'eau situé au dessus est alors, sur plusieurs centaines de kilomètres
brusquement déplacée.
La perturbation ainsi créée se déplace sur plusieurs centaines de km et
met plusieurs minutes à plusieurs heures avant d'atteindre les côtes.
La NOAA a mis en place un réseau qui permet de détecter les mouvements
des fonds océaniques ghrâce à des capteurs de pression : le signal est
envoyé par onde sonore vers une bouée en surface, qui envoie,
immédiatement, sous forme d'onde radio, les informations au centre de
contrôle d'Hawaï via un satellite géostationnaire.
1. Identifier, au
sein du dispositif décrit dans l'énoncé, les différentes ondes qui
interviennent, en précisant leur milieu de propagation.
2. Ces pondes
sont-elles toutes mécaniques ? Si oui, laquelle ou lesquelles ?
Préciser si elles sont longitudinales ou transversales.
Dans
l'océan, propagation d'une onde mécanique longitudinale ( onde sonore).
De
la bouée vers le satellite et du satellite au centre de contrôle : onde
électromagnétique se propageant dans l'atmosphère et dans le vide.
3. Expliquer
pourquoi les ondes radio peuvent être utilisées dans ce dispositif.
Les ondes radio se propagent dans l'air et dans le vide à la célérite c
= 3 108 m/s.
Les ondes radio ne sont pas absorbées par l'atmosphère.
4. Quelle est la
durée Dt
nécessaire à la transmission d'une information entre le capteur de
pression et la bouée en surface si la distance qui les sépare est de 30
km.
Célérité des ondes sonores dans l'eau v = 1500 m /s.
Dt =
30 000 / 1500 = 20 s.
5. La distance
bouée-satellite est D = 3,6 104 km. Quelle est la durée Dt' nécessaire à la
transmission d'une information entre la bouée et le satellite ?
Dt' = 3,6 107 /
(3 108) =0,12 s.
6. En déduire l'ordre de grandeur du
temps séparant la détection du tsunami et le déclenchement de l'alerte.
Conclure sur l'efficacité de ce dispositif.
20 +0,12 +durée de transmission entre le
satellite et le centre de contrôle.
Donc moins d'une minute. Ce dispositif est très éfficace.
|
|