Skieur, prisme, canon à électrons. Concours Orthoptie Montpellier 2017. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . III. Skieur. Un skieur assimilé à un point matériel M, de masse m = 80 kg, part avec une vitesse nulle du point S, situé à une hauteur hS = 540 m, pour arrivé au point O, situé à une hauteur h0 = 491 m. Le tracé So correspond à un arc de cercle de rayon r. Le long de la piste SO, les frottements entre la piste et les skis ainsi que l'action de l'air sont négligés.  La référence de l'énergie potentielle est choisie au point  O. g = 10 m s-2 ; OA = 5,0 m. 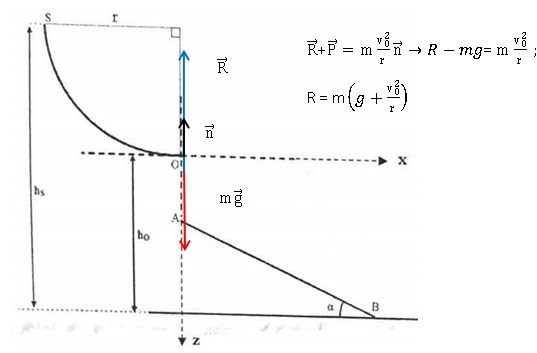1. Déterminer la longueur de la piste SO. r = hS-hO = 540-491 =49 m ; SO = pr / 2 =3,14 x49 / 2 ~ 76,97 ~77 m. 2. Donner l'expression de l'énergie mécanique du skieur en S et en O en fonction des données. En S, l'énergie mécanique est sous forme potentielle : mg(hS-hO). En O l'énergie mécanique est sous forme cinétique : ½mv02. 3. En déduire les caractéristiques du vecteur vitesse en O. Ce vecteur est tangent à l'arc de cercle en O ( horizontale) et a le sens du mouvement ( vers la droite).  Ecrire la conservation de l'énergie mécanique : Sa norme vaut v0= (2g(hS-hO))½ = (20 x49)½ =31,3 m /s. 4. Déterminer la valeur de la réaction normale agissant sur le skieur en O. R = m(g+v02/r) = 80(10+31,32/49)=2,4 103 N. 5. En O, le skieur quite la piste avec une vitesse v0. Déterminer l'équation de la trajectoire suivie par le skieur dans le repère donné. Le mouvement est une chute libre avec une vitesse initiale horizontale v0. Accélération ( 0 ; g) ; la vitesse est une primitive de l'accélération : vx = v0 ; vz = gt. La position est une primitive de la vitesse : x = v0t ; z = ½gt2. Trajectoire : z = ½gx2 / v02 =5 /980 x2=0,0051 x2. 6. Le skieur atterit au point P sur le plan incliné AB, faisant un angle a = 40° avec l'horizontale. Déterminer les coordonnées du point P. Equation de la droite (AB) : z = tan 40 x +zA  ; z = 0,839x +5. Coordonnées du point P : 0,0051 x2=0,839x +5 ; 0,0051 x2-0,839x -5=0 ; discriminant D = 0,8392 +4 x0,0051 x5 = 0,806 ; D½ = 0,8977. On retient la racine positive : xP=(0,839 +0,8977) / (2x0,0051) =170,27 ~ 170 m. yP = 0,839 x170,27 +5 ~148 m. IV. Prisme   Un prisme d'indice n' = 1,45, est situé dans l'air ( indice n=1). La section principale de ce prisme est un triangle ABC. Un faiscerau de lumière arrive au niveau de l'interface AB et ressort au point F.   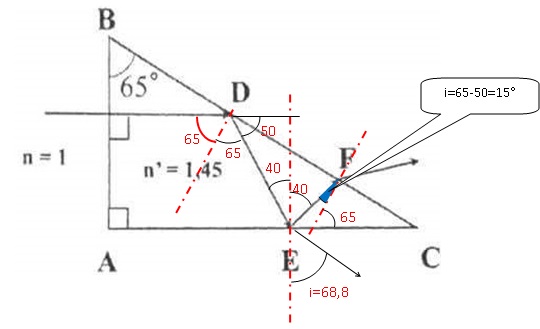Q1. Une partie du rayon lumineux émerge-t-elle au point D ? Justifier. Dans l'hypothèse d'une réfraction en D, l'angle réfracté i est tel que :  sin i = 1,45 sin 65 = 1,314, c'est impossible. L'hypothèse est fausse : en D, il y a réfrlexion totale. Q2. En E quel est l'angle d'incidence du rayon lumineux sur l'interface AC ?. 40° ( voir schéma ci-dessus) Q3. En E la lumière se propage-t-elle par réflexion totale , Justifier. Dans l'hypothèse d'une réfraction en E, l'angle réfracté i est tel que :  sin i = 1,45 sin 40 = 0,932, valeur inférieure à 1 ; i =68,8°. L'hypothèse est vraie. Q4.   Quel est l'angle de réfraction en F ? l'angle d'incidence vaut 15°. 1,45 sin 15 = sin r ; sin r = 0,375 ; r = 22,0°. Q5. Pour que la lumière se propage par réflexion totale au point D, quel est l'indice de réfraction du milieu n qui ne doit pas être dépasé ? A la limite de la réflexion totale : n  sin r =n sin 90 = n = 1,45 sin 65 =1,314. n doit être inférieur à 1,314 pour qu'il y ait réflexion totale en D. V. Canon à électrons.  On applique entre l'anode et la cathode d'un canon à électrons une tension UAC = 1000 V. On obtient un faisceau d'électrons homocinétique qui pénètre en O dans un champ électrique uniforme engendré par deux plaques parallèles P et P' soumise à une tension UPP' = 200 V. La longueur l de chaque plaque et la distance d qui les sépare valent 4 cm. L'écran fluorescent est situé à la distance L =OO' = 50 cm.   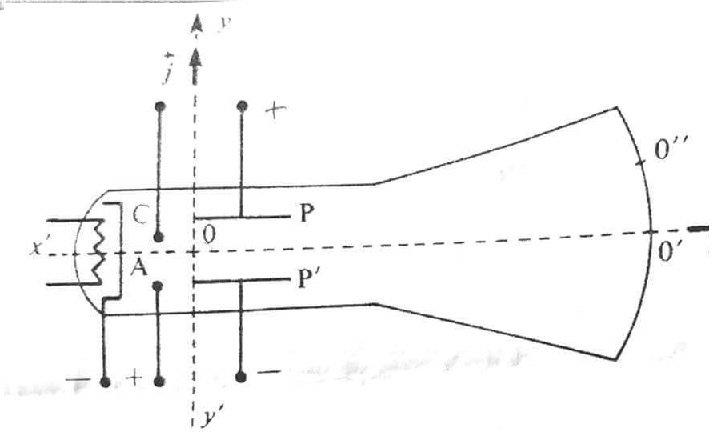Q1. Déterminer la vitesse v0 des électrons au point O. Le poids des électrons est négligeable devant la force électrique. La vitesse initiale des électrons est négligeable. Théorème de l'énergie cinétique entre cathode et O : ½mv02 = eUAC ; v0 = ( 2eUAC / m)½ = (2 x 1,6 10-19 x1000 /(9,1 10-31))½=1,875 107 ~1,9 107 m/s. Q2. Etablir les équations du mouvement des électrons entre les plaques P et P' ainsi que l'équation de la trajectoire. 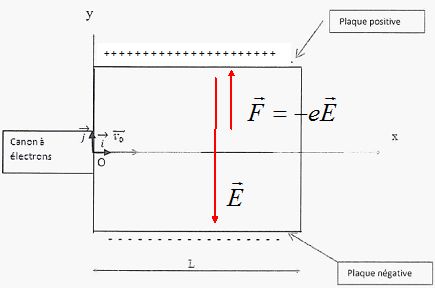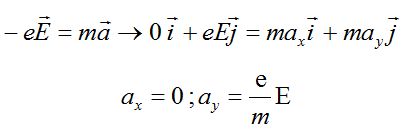La vitesse est une primitive de l'accélération : vx = v0 ; vy = eE/m t. La position est une primitive de la vitesse et la position initiale est l'origine O du repère. x = v0t ; y = ½eE/mt2. Equation de la trajectoire : y = eEx2 /(2mv02). Q3. Calculer la distance D du spot sur l'écran fluorescent. 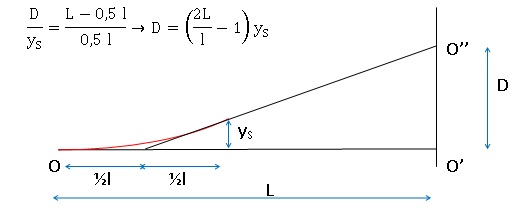yS = eE l2 /(2mv02)= eUPP' l2 /(2mdv02)=eUPP' l /(2mv02) ; yS =1,6 10-19 x200 x0,04 /(2x9,1 10-31 x3,52 1014) = 2,0 10-3 m. D = (2x0,50 /0,04 -1)x2,0 10-3 =  0,048 m = 4,8 cm. .

menu