QCM Physique.
Concours ergothérapie Créteil 2016.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Durée 20 minutes ( 6 points).
Q1.
Au cours d’une séance d’exercice physique, un patient lance une balle
vers le haut depuis la surface terrestre avec une vitesse initiale v0
; cette balle atteint une altitude maximale de 12 m. On néglige tout
frottement. Sachant que la pesanteur lunaire est le 1/6 de la pesanteur
terrestre, quelle serait l’altitude maximale atteinte par la balle,
lancée depuis le sol lunaire avec la même vitesse initiale ?
a) 8 m ; b) 14 m ; c) 72 m ; d) 94 m ; e) 132 m ; f) aucune bonne réponse.
La conservation de l'énergie mécanique de la balle conduit à
v02 = 2gh ; h = v02 / (2g) ;
Sur terre : v02 = 2 x10x12 = 240 ; sur la lune h = 240 x 6 / (2 x10)=72 m.
Q 2.
Un système de rééducation d’un patient comporte un ressort attaché à un point fixe, qui soutient à
son autre extrémité un poids qui allonge le ressort de 40 cm. Calculer la période des oscillations
harmoniques (non amorties) de ce système, dans le Système International.
a) 0,25 ; b) 1,25 ; c) 0,75 ; d) 2,5 ; e) 1,75 ; f) aucune bonne réponse.
m g = 0,4 k, avec k raideur du ressort ; m / k = 0,4 / 10 = 0,04.
T = 2p (m / k)½ = 6,28 x0,04½ = 6,28 x0,2 =1,256 s.
Q 3.
Au cours d’une cure thermale, le médecin vous a conseillé de prendre un bain à 35°C.
Vous décidez de faire couler 100 L d’eau à 85°C puis vous ajoutez un
volume V d’eau froide à 10°C. Si l’on néglige les pertes thermiques
dans l’air ambiant et la capacité thermique de la baignoire, on peut
dire que V (en L) vaut :
a) 75 ; b) 125 ; c) 175 ; d) 150 ; e) 200 ; f) aucune bonne réponse.
Energie gagnée par l'eau froide : Q= V reau ceau (35-10 )=25V reau ceau.
Energie cédée par l'eau chaude : Q'= 100 reau ceau(35-85 )= -5000 reau ceau.
Q +Q' = 0 ; 25V reauceau -5000 reauceau= 0 ; V = 200 L.
|
|
|
Q 4
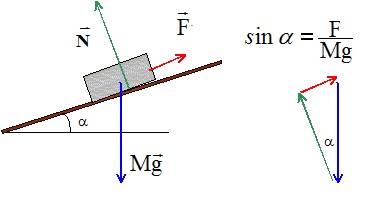
Une ergothérapeute s’intéresse à la pente d’une rampe d’accès, pour le
fauteuil roulant électrique de sa patiente : pour cela elle cherche à
évaluer l’angle a
que fait le plan incliné avec l’horizontale. La praticienne considère
qu’elle peut négliger les frottements et que le mouvement pendant la
montée est rectiligne et uniforme. On note F la force motrice du
fauteuil et N la réaction du plan incliné. On note m la masse du
système {fauteuil + patiente} ; on peut affirmer que :
a) sin a = F/(mg) ; b) cos a = F/(mg) ; c) 2 forces s’exercent sur le système ;
d) sin a =N/(mg) ; e) tan a =F/N ; f) aucune bonne réponse.
|
|
|
|
Q 5.
Le fauteuil électrique de la question 4 est alimenté notamment grâce à un générateur. Ce générateur
linéaire de courant continu a une tension à vide E = 30V et une résistance interne r = 6 ohms et fournit
une puissance de 31,5 W au circuit extérieur résistif. On peut affirmer que les valeurs possibles pour
l’intensité du circuit, en A, sont respectivement :
a) 7,5 et 3 ; b) 1 et 2,5 ; c) 1 et 7,5 ; d) 1 et 5 ; e) 2 et 3,5 ; f) aucune bonne réponse.
U = E-rI = 30-6I.
P = UI= (30-6I) I = 31,5.
6I2-30I +31,5 =0.
D = 302 -4 x6x31,5 = 900-756 =144. D½ = 12.
I = (30 +12) / 12 = 3,5 ; I = (30 -12) / 12 = 1,5.
Q 6.
La sirène d’une ambulance émet une onde sonore de fréquence f = 400 Hz. L’onde sonore se propage
dans l’air à la célérité c = 340 m.s-1. L’ambulance se déplace avec un mouvement rectiligne uniforme
de vitesse constante v = 72 km.h-1 vers un observateur fixe. La fréquence f ’ perçue par l’observateur
a pour valeur (en Hz) :
a) 385 ; b) 425 ; d) 450 ; e) 530 ; f) aucune bonne réponse
f ' = f / (1-v/c) avec v = 72 /3,6 =20 m / s.
f ' = 400 /(1-20 /340) = 400 x340 / 320 = 425 Hz. |
|