Mécanique, satellite géostationnaire, concert et niveau sonore
  Concours audioprothésiste Paris 2017 .

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .



.
.


Wagonnet d'exploitation minière.
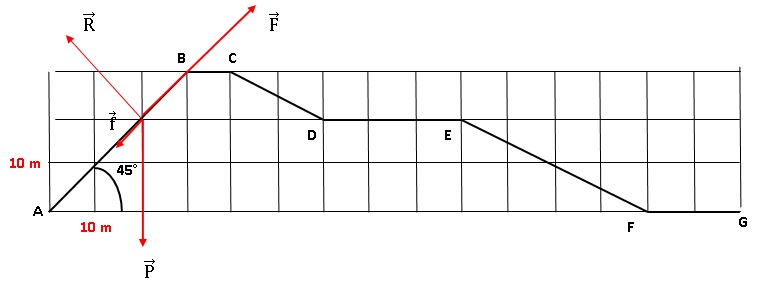
Le wagonnet suit le parcours représenté ci-dessous.
Il ne possède pas de moteur et est simplement équipé d'un frein automatique.
Les frottements sont considérés comme constants tout le long du parcours, de sens opposé au déplacement et de valeur f = 600 N.
Masse du wagonnet  m = 500 kg ; g = 9,81 m s-2.

1. Une crémaillère hisse le wagonnet de A en B en 25 s. la vitesse finale en B est la même que la vitesse initiale en A. Quelles sont les énergies et puissance nécessaires à la montée du wagonnet ?
Ecrire le théorème de l'énergie cinétique entre A et B.
DEc = 0 ;
La force R ne travaille pas, elle est constamment perpendiculaire au déplacement.
Travail résistant des frottements : -f AB = -600 x 30 / cos 45 = -2,55 104 J.
Travail résistant du poids en montée : -mg x30 = -500 x9,81 x 30 = -1,47 105 J
Travail de F = 2,55 104 +1,47 105 = 1,73 105 J.
Puissance mise en jeu = énergie / durée = 1,73 105 / 25 = 6,90 103 W.
2. De B à C un moteur extérieur, par le biais d'un câble horizontal, déplace le wagonnet à vitesse constante de 2 m/s. Quelle est la valeur FM de la force motrice ? Quelle est la puissance mécanique du moteur ?
Entre B et C le mouvement est rectiligne uniforme. D'après la première loi de Newton la somme vectorielle  des forces appliquées au wagonnet est nulle.
Le poids est opposé à l'action normale du plan ; la force motrice est opposée au frottement. FM = 600  N.
Puissance mécanique = force motrice fois vitesse = 600 x2 = 1,2 103 W.
3. Arrivé en C le wagonnet est stoppé par freinage, puis il est lâché dans la pente sans vitesse initiale. Entre D et E aucune action n'est réalisée. Calculer la vitesse du wagonnet en D, en E puis en F.
Entre C et D, l'énergie cinétique varie de ½mvD2-0.
Travail moteur du poids en descente : 10 mg = 10 x500 x9,8 =4,905 104 J.
Travail résistant des frottements : -f CD = -600 x(102 +202)½ =  -1,342 104 J.
Somme des travaux des forces : 3,563 104 J.
Ecrire le théorème de l'énergie cinétique entre C et D : vD = (2 x3,563 104 / 500)½ =11,94 ~11,9 m s-1.
Entre D et E, l'énergie cinétique varie de ½mvE2-½mvD2.
Le poids ne travaille pas, il est perpendiculaire au plan.
Travail résistant des frottements : -f DE = -600 x30 =  -1,8 104 J.
Ecrire le théorème de l'énergie cinétique entre D et E :
½mvE2=½mvD2-f DE = 3,563 104 -1,8 104 =1,763 104 J.
 vE = (2 x1,763 104 / 500)½ =8,397 ~8,4 m s-1.
Entre E et F, l'énergie cinétique varie de ½mvF2- ½mvE2.
Travail moteur du poids en descente : 20 mg = 20 x500 x9,81 =9,81 104 J.
Travail résistant des frottements : -f EF = -600 x(202 +402)½ =  -2,683 104 J.
Somme des travaux des forces : 7,127 104 J.
Ecrire le théorème de l'énergie cinétique entre E et F :
½mvF2=½mvE2+7,127 104  = 250 x8,3972 +7,127 104  =8,89 104.
vF = (2 x8,89 104 / 500)½ =18,86 ~18,9 m s-1.

4. A partir de F, des freins sont actionnés pour arrêter le wagonnet exactement en G. Quelle est la valeur de la force de freinage, supposée constante, pour arrêter le wagonnet en G ?
Entre F et G, l'énergie cinétique varie de 0-½mvF2.
Le poids ne travaille pas, il est perpendiculaire au plan.
Travail résistant des frottements : -f FG = -600 x20 =  -1,2 104 J.
Travail résistant de la force de freinage -20F
Ecrire le théorème de l'énergie cinétique entre F et G :
½mvF2= 1,2 104 +20 F=250 x18,862 =8,89 104.
20F = 8,89 104 -1,2 104 = 7,69 104 ; F = 3,84 103 N.
....

.....
 Satellite de télécommunication.
On considère un satellite de télécommunication de masse m en orbite géostationnaire. Son mouvement est étudié dans le référentiel géocentrique.
6.1. Définir ce qu'est le référentiel géocentrique. Quelle est la période de révolution de la terre ? Quelle est sa période de rotation propre ?

Le référentiel héliocentrique a pour origine le Soleil et des axes pointant vers des étoiles lointaines qui paraissent fixes.
Le référentiel géocentrique a pour origine le centre de la Terre et des axes parallèles à ceux du référentiel héliocentrique.

La période orbitale de la terre est de 365 jours 5 heures et 46 minutes. La période de rotation propre de la terre est de 24 heures.

2. Indiquer la forme de la trajectoire du satellite et le plan dans lequel elle est située. Quelle est la vitesse angulaire du satellite ? Quel est son mouvement dans le référentiel terrestre ? Pour l'étude du mouvement du satellite, le référentiel terrestre peut-il être considéré comme galiléen ?
Dans le plan équatorial, la trajectoire est un cercle.
Le satellite tourne dans le même sens que la terre et avec la même vitesse angulaire que la terre soit :
w=2 p / (24 x3600) = 7,29 10-5 rad /s.
Le satellite paraît fixe pour un observateur terrestre.
On peut considérer le référentiel terrestre comme galiléen si l'on se situe près de la surface de la terre et si la vitesse du corps étudié est assez faible.
 3. L'altidude du satellite est égale à 35 800 km. Calculer le rayon r de sa trajectoire. Caractériser la direction et le sens du vecteur vitesse du centre d'inertie du satellite et donner la valeur de v en km /s.
Rterre = 6380 km.
r = 6380 +35800 = 42180 km.
Le vecteur vitesse est tangent à la trajectoire circulaire ; il a le sens du mouvement.
v = w r =7,29 10-5 x 42180 = 3,075 ~3,1 km /s.
 4. Caractériser la direction et le sens du vecteur accélération. Exprimer sa valeur a en fonction de v et r. Calculer a dans le système SI.
Le vecteur accélération est centripète ( dirigé vers le centre de la terre).
a = v2 /r = .(3,075 103)2 / (42180 x1000 ) = 0,224 m s-2.




5. On considère que le référentiel géocentrique est galiléen et que la seule force subie par le satellite de masse m est la force de gravitation exercée par la terre de masse M. Exprimer v en fonction du rayon r et du produit GM. En déduire l'expression de la troisième loi de Kepler.
v =(GM /r)½.
Le satellite décrit la trajectoire circulaire 2pr à la vitesse v en T seconde.
2pr = vT ;  4 p2 r2 = v2 T2 = GMT2 / r ; T2 / r3 =4 p2 /(GM).
6. Calculer la valeur du produit GM.
GM = 6,67 10-11 x5,97 1024 = 3,98 1014 m3 s-2.
7. Vérifier la valeur obtenue sachant que g = 9,81 m s-2 au niveau du sol.
g = GM / R2 ; GM = g R2 = 9,81 x(6380 x1000)2 = 3,99 1014 m3 s-2.
8.. Pour effectuer la mise en orbite géostationnaire du satellite, celui-ci est d'abord placé en orbite d'attente après avoir été largué par le dernier étage d'une fusée. Sur cette orbite elliptique dont la terre est l'un des foyer, l'altitude minimale du satellite est zP = 200 km au point P et l'altitude maximale zA atteinte au point A est celle de l'orbite géostationnaire.
Représenter l'orbite du satelluite autour de la terre et y placer les points A et P. Déterminer la demi-longueur du grand axe de l'ellipse.

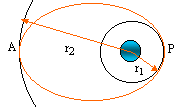
a = ½(zP +zA) +R = 0,5 (200 +35800) +6380 =2,438 104 ~2,44 104 km.

9. En quels points de la trajectoire la vitesse du satellite est-elle la plus grande ? la plus petite ? Justifier.

v = (GM / r)½.

La vitesse est la plus grande au point P ( rP < rA).

10. Donner l'expression de la période orbitale T du satellite. Calculer T et le temps mis par le satellite pour passer du point P au point A.
T2 = 4p2 a3 /(GM) = 4 x3,142 x(2,438 107)3 / (3,98 1014) =1,44 109 ; T = 3,79 104 s.

Durée du passage de P en A : 0,5 T = 1,89 104 s










Concert et niveau sonore.
Un concert est donné avec deux violons. Un sonomètre placé à 5 m des musiciens mesure le niveau d'intensité sonore produit séparément par chacun des deux instruments. Les mesures donnent L1 = 75 dB et L2 = 80 dB.
1. Déterminer les intensités sonores I1 et I2 émises respectivement par chaque instrument à la distance de  5 m.
I1 = 10-12 x 107,5 = 3,16 10-5 W m-2.
I2 = 10-12 x 108 = 1,0 10-4 W m-2.
2. Quelle est l'indication du sonomètre placé à 5 m si les musiciens jouent simultanément ?
Itotal = 3,16 10-5 +1,0 10-4 =1,316 10-4 W m-2.
L = 10 log ( 1,316 10-4 / 10-12) = 81,2 dB.
3. Combien de violons, produisant chacun en un point un son de niveau sonore 80 dB, faudrait-il pour que le niveau d'intensité sonore résultant en ce point soit  de 100 dB ?
Itotal = 10-12 x 1010 =10-2  W m-2.
Pour un seul violon I2 =   1,0 10-4 W m-2.
Il faut donc 100 violons situés au même point.
4. Quel serait le niveau d'intensité sonore produit par tous ces violons, à une distance de 10 m du point d'émission ? A la distance de 20 m ? On admettra qu'il n'y a pas de perte d'intensité sonore, ni de réflexion sur le sol.
I = d2 = Constante.
Si la distance double, l'intensité sonore est divisée par 4.
A 10 m : I = 10-2 / 4 = 2,5 10-3 W m-2.
L = 10 log(2,5 10-3 / 10-12) ~94 dB.
Si la distance quadruple, l'intensité sonore est divisée par 16.
A 20 m : I = 10-2 / 16 = 6,25 10-4 W m-2.
L = 10 log(6,25 10-4 / 10-12) ~88 dB.

 

.


  

menu