QCM laser,
mécanique.
Concours audioprothèsiste Bordeaux 2017.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Une
seule réponse juste par question. Des points négatifs seront affectés
en cas de réponses fausses..
22. Un laser He-Ne émet un faisceau
en continu d'une puissance 1 mW de longueur d'onde l = 633 nm. Ce laser émet
par seconde :
6 1019 photons ; 2 1030
photons ; 2 1036
photons ; 3 1015 photons ; 4 1017 photons.
Energie d'un photon : 6,63 10-34 x 3 108 /(633 10-9)
= 3,14 10-19 J
Nombre de photons émis en une seconde : 10-3 / (3,14 10-19)
~3 1015.
23. Dans le lecteur DVD blu-ray, l'utilisation d'un
laser bleu permet :
A. de diminuer la consommation électrique du lecteur.
B. d'augmenter la puissance et donc la rapidité de lecture.
C. d'augmenter la capacité de stockage d'information. Vrai.
D. de rendre le lecteur plus silencieux.
E. permet de stocker l'information en profondeur dans le disque.
24. L'acronyme
LASER signifie.
A Light Amplification by Solitonic Electron Resonance.
B. Light Absorption by
Stimulated Emission of Radiation.
C. Light Amplification by Stimulated Emission of
Radiation. Vrai.
D. Light Alteration by Stimulated
Emission of Radiation.
E. Light Absorotion by Stimulated Emission of Resonance.
25.
En
observant une bulle de savon, on voit apparaître des irisations dont
les couleurs changent suivant l'angle d'observation.
Une bulle de savon est constituée d'un mince film d'eau savonneuse
emprisonnant de l'air. Quand la lumière travers le film, il se produit
un phénomène d'interférences entre la lumière rfléchie sur la face
extérieure du film et celle réfléchie par la face intérieure. Pour un
angle d'incidence très faible, la différence de marche entre les ondes
qui interfèrent s'écrit :
d =
2ne+½l .
avec n = 1,3 indice de l'eau savoneuse et l longueur d'onde de la
lumière incidente.
A. Les
ondes qui interfèrent peuvent être qualifiées de cohérentes car
l'épaisseur e du film est très faible ainsi que l'angle.
B. Pour que la bulle apparaisse rouge, il faut que e = 0,125 µm. Vrai.
d = kl = 2ne+½l
avec k entier relatif ; l(k-0,5)
= 2 x1,3 e. lR
=680 nm
e=0,680(k-0,5) /2,6 ~0,2615 (k-0,5) ;
si k = 1 , e = 0,13 µm.
C. Les interférences sont constructives si e = l / (2n).
D. Pour que la bulle apparaisse rouge, il faut que e ~0,062 µm.
E. Pour que
la bulle apparaisse verte, il faut que e ~0,125 µm.
26.
L'énergie E a pour équation aux dimensions :
MT-2 ; AT ; MLT ; ML2T -2 ; L2T -2.
27.
Le champ de pesanteur g a pour équation aux dimensions :
L2 T-2 ; L T -2 ; MLT ; MLT -2 ; M.
28. Considérons l'expression
suivante : exp(hn
/ (kT) -1 où h désigne la constante de Planck, n une fréquence et T la
température.
Dans le système international, k s'exprime en :K-1 ; J K ; N
m K-1 ; sans unité ; J K-1.
hn
/ (kT) est sans dimension et hn
est une énergie en joule.
29.
Soit un tronc conique de hauteur h, de rayons r et R. Trouver la
formule qui donne son volume à l'aide d'une analyse dimensionnelle.
V = 2p (R-r)h /3.
Faux. V en m3 non homogène à (R-r)h en m2.
V = p
(R2+rR+r2)h /3. Vrai.
V en m3 homogène à (R2+rR+r2)h en m3.
V = p (R2-R+r2)h
/3. Faux. R2-R+r2 non homogène.
V = p
(r-r/R)2h /3. Faux. r-r / R non homogène.
V = p (R2+rR+r2)h
/ (3r). Faux. V en m3 non homogène à (R2+rR+r2)h
/ (3r) en m2
|
|
|
30.
Soit une particule élémentaire de masse m, de quantité de mouvement p
et d'énergie E. Trouver la formule qui relie ces grandeurs ( c :
vitesse de la lumière dans le vide ) à partir d'une analyse
dimensionnelle.
E = mc2
+p2 / (2m2). Faux, p2 / (2m2) non homogène à une
énergie.
E = [pc2 +m2c4]½. Faux, pc2 non homogène au carré d'une énergie.
E2 = p2c2 +m2c4.Vrai.
E2 = p2c2
/ m +m4. Faux.
E = p2c2
+m2c4. Faux.
31. Dans le système CGS ( cm, g, s)
l'énergie s'exprime en erg. Combien de joule vaut 1 erg ?
10-7 ; 10-5 ; 10-3
; 105 ; 107.
Joule = kg m2 s-2 = 103 g x104
cm2 s-2 = 107 g cm2
s-2 = 107 erg.
32.
La période d'oscillation d'un pendule simple dépend
de sa longueur L, du champ de pesanteur g et de l'amplitude qmax des
oscillations. On propose plusieurs formules.
Précisez quelles sont les formules inhomogènes.
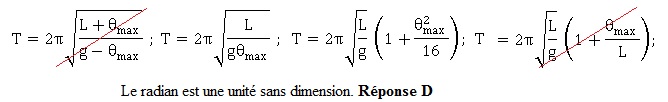
33. L'impédancemétrie
tympanique est une technique utilisée en audiométrie pour aider à
diagnostiquer les pathologies au niveau de l'oreille moyenne. Elle
consiste à mesurer l'admittance acoustique Y dont la formule
théorique pour un volume clos V est : Y = Vw /(rc2) en mhoa.
w
pulsation en rad s-1 ; r : masse volumique de l'air
1,2 kg m-3 ;
c = 340 m /s, vitesse du son dans l'air.
Ce test est généralement réalisé à la
fréquence de 226 Hz. Calculet Y si V = 1 mL.
10-4mhoa ; 1 µmhoa ; 10-8 mhoa
; 1 mmhoa ; 10 cmhoa.
Y =10-6 x2 x3,14 x226 /(1,2 x3402)=1,0
10-8 mhoa.
34. Les praticiens
ont souvent l'habitude de raisonner non pas dans le système
internationnal (mks) mais dans le système cgs. Trouver l'équivalence
entre les deux système.
Y = m3 s-1 kg-1 m3 m-2
s2 = kg-1 m4 s =10-3
g-1 x 108 cm-2 s =105 g-1 cm-2 s .
1 mhoa(cgs) = 10-5 mhoa(mks). Réponse A.
35. L'admittance
acoustique d'un volume de 1 cm3 à la fréquence 226 Hz vaut
dans le système cgs : Y =1,0
10-8 mhoa (mks) = 1,0
10-3 mhoa (cgs)= 1 mmhoa(cgs).
Réponse E.
|
|
|
|
36. Lorsqu'on étudie la réponse en
fréquence d'un système en électronique ou en acoustique, on a
l'habitude de l'exprimer dans un diagramme semi-logarithmique dans
lequel l'axe des fréquences ou des pulsations est exprimé de manière
logarithmique.
En électronique, la pente des courbes est exprimée en dB/décade où une
décade représente une multiplication par 10 de la fréquence.
En acoustique la pente des courbes est exprimée en dB/octave où une
octave représente une multiplication par 2 de la fréquence.
log 2 / log 10 ~0,3.
Une pente de -20 dB / décade est équivalente à une pente de : 20 x0,3 =
-6 dB /octave. Réponse B.
37. On considère un réseau Wi-Fi
pour lequel les données sont transmises à la fréquence de 2,4 GHz.
A. la longueur
d'onde du signal dans l'air est environ 100 m.
3 108 / (2,4 109) =0,125 m.
B. Une image
numérique en couleur occupe une place mémoire de 1,08 Mbits. La durée
de transfert, par ce réseau, de cette image sera de 20 ms.
Débit : 54,0 Mbits / s.
1,08 /54,0 = 0,02 s = 20 ms. Vrai.
C. La vitesse de
transmission du signal numérique est c, vitesse de la lumière dans le
vide.
D. On considère une
image numérique en couleur au format bmp de format (2560 pixels x 1920
pixels ). La taille de l'image est approximativement 4,92 Mo.
Chaque pixel est codé sur 4 octets au format bmp.
4 x2560 x1920 =1,97 107 octets = 19,7 Mo.
E. En codage RVB
sur 3 octets, un pixel d'une image est encodée avec le code
111111110000000011111111 et ce pixel est de couleur cyan.
Le rouge et le bleu ont la même intensité ; le vert est absent. Le
pixel est magenta.
.
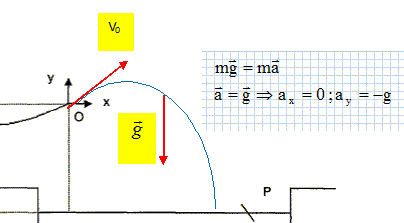
38. Un enfant glisse le long d'un
tobogan de plage dans le référentiel terrestre supposé galiléen.
L'enfant est assimilé à son centre d'inertie G et on néglige tout
frottement.

La vitesse initiale en D est nulle. La vitesse en O, notée v0, fait un angle a =30° avec l'horizontale.
Masse de l'enfant m = 35 kg ; h = 5 m ; H = 0,5 m.
On choisit le point O comme référence de l'énergie potentielle de
pesanteur. On consodère le temps t=0, l'instant où l'enfant est en O,
origine du repère. L'énergie mécanique de l'enfant au point O est :
mgh ; 0 ; mg(h+H) ; mgH ; mgh +½mv02.
Energie mécanique en D : mgh.
Energie mécanique en O : ½mv02.
L'énergie mécanique se conserve.
39. La vitesse de l'enfant en O est en m/s : 3,1 ; 9,9 ; 8,6 ; 4,9 ; 10,4.
½mv02=mgh ; v0 = (2gh)½ =(2 x9,8 x5)½ = 9,9 m /s.
40.
L'énergie mécanique de l'enfant au point P est :
mgh ; 0 ; mg(h+H) ; mgH ; mgh +½mv02.
L'énergie mécanique se conserve ; elle a même valeur en D qu'en P et vaut : mgh.
41. L'équation de la trajectoire de l'enfant entre O et P est :
Le vecteur vitesse est une primitive de
l'accélération.
vx = constante ; la constante est égale
à la vitesse initiale projetée sur l'axe des
x.
vx = v0 cos
a.
vy = -gt constante ; la constante est
égale à la vitesse initiale projetée
sur l'axe des y.
vy = -gt + v0
sin a.
Le vecteur position est une primitive du vecteur vitesse.
L'enfant étant à l'origine du repère
à la date t = 0, les constantes d'intégration
seront nulles.
x = v0 cos
a
t.
y = -½gt2 +
v0 sin at.
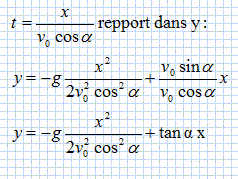 Réponse E. Réponse E.
42. La vitesse de l'enfant en P est en m/s : 3,1 ; 9,9 ; 8,6 ; 4,9 ; 10,4.
Conservation de l'énergie mécanique : mgh = -mgH +½mvP2.
vP =(2 g(h+H)½=(2 x9,8 x5,5)½=10,4 m/s.
43. L'abscisse x de P est en m :3,1 ; 9,9 ; 8,7 ; 9,5 ; 0,8.
y = -9,8 x2 / (2*9,92
*cos230) + x tan 30.
y = -6,67 10-2 x2 + 0,577 x.
Au point P, y = -H = -0,50 m
-0,50 = -6,67 10-2 x2 + 0,577 x.
6,67 10-2 x2 - 0,577 x -0,50 = 0
x2 -8,66 x -7,5 =0
discriminant D = 8,662+4*7,5 = 104,92 ; D
½=10,24.
x1 = ½(8,66- 10,24) , valeur
négative à ne pas retenir.
xP = ½(8,66+10,24)~9,5 m.
44. Le point le plus haut de la trajectoire entre O et P ( la flèche ) est atteinte par l'enfant au temps t ( en seconde) :
1,1 ; 0,90 ; 0,51 ; 0,34 ; 0,21.
Au sommet vy=0 = -gt +v0 sin 30 ; t = 9,9 x0,5 / 9,8 =0,5051~0,51 s.
45. L'ordonnée de la flèche est en m : 1,3 ; 1,6 ; 0,82 ; 0,95 ; 1.
y = -½gt2 +
v0 sin at. =-4,9 x0,50512 +9,9 xsin 30 x0,5051 ~1,25 m
46. L'abscisse de la flèche est en m : 4,8 ; 4,3 ; 3,9 ; 3,5 ; 2,8.
x = v0 cos
a
t=9,9 x cos 30 x0,5051 = 4,3 m.
47. Un mur thermique de surface S et d'épaisseur e est constitué d'un matériau de conductivité thermique l. Quelle est sa résistance thermique R ?
R = e / (l S). Réponse B.
|
|