Mathématiques, Preparation au concours ingénieur territorial 2019

Mathématiques, Préparation au concours ingénieur territorial 2019.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

Résoudre dans R.
1. x³-4x²+x=0.
x(x²-4x+1)=0 ; :
Solutions réelles de x²-4x+1=0.
D = (-4)² -4 = 12 ; D^½ = 2 x3^½ .
x₁ = (4 + 2 x3^½) / 2 = 2 +3^½ ; x₂ =2-3^½.
Solutions x=0, x = 2 +3^½ et x=2-3^½.
2. 7x-6 < x².
x²-7x+6 > 0.
Solutions de x²-7x+6 =0.
D = (7)² -6x4 = 25 ; D^½ =5.
x₁ = (7 + 5) / 2 = 6 ; x₂ =(7-5) / 2 = 1.
Solutions de 7x-6 < x².
] -oo ; 1 ] et [7 ; +oo[.

Nombres complexes.
1. Donner la forme algébrique puis la forme trigonométrique, dans C, de z = (3+i)(2i-1).
z = 6i-3+2i²-i= -5+5i.
Module de z : |z| = [(-5)² +5²]^½ = 5 x2^½.
z / |z| = -2^½ / 2 + 2^½ / 2 = cos (3p/4) +i sin ( 3 p/4).
z = 5 exp(3ip/4).
2. Résoudre dans C. ( on donnera la forme algébrique de la solution).
a. 2iz +3 = 1 -5z.
z(2i+5) = -2 ; z = -2 /(2i+5) = -2(5-2i) / 29=(4i-10) / 29.
b. z²+4z+6=0.
D =4²-24 = -8 =8i². D^½ = 2 i x2^½.
z₁=(-4 +2 i x2^½) / 2 = -2+i x 2^½ ; z₂ = -2 +i x2^½.

....

...
Analyse.
1. Déterminer la fonction dérivée de la fonction définie sur ]0 ;+oo[ par :
g(x) = cos (3x+1) +x ln (x)-x+1.
Dérivée de cos (3x+1) : -3 sin (3x+1).
Dérivée de x ln(x).
On pose u = x et v = ln(x) ; u' = 1 et v' = 1 /x ; u'v+v'u = ln(x) +1
g'(x) = -3 sin(3x+1)+ln(x)+1-1=-3 sin(3x+1)+ln(x).
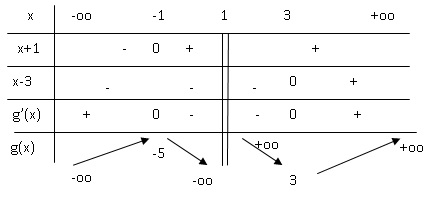
2. Dresser le tableau de variations de g fonction définie sur R-{1} par :
g(x) = (x²-3x+6) / (x-1).
On pose u =x²-3x+6 et v =x-1.
u'=2x-3 ; v' = 1 ;
g'(x) = (u'v-v'u) / v² =[(2x-3)(x-1) -x²+3x-6)] /(x-1)²=(x²-2x-3) /(x-1)².
g'(x) =(x-3)(x+1) / (x-1)².

3. Calculer les intégrales suivantes :

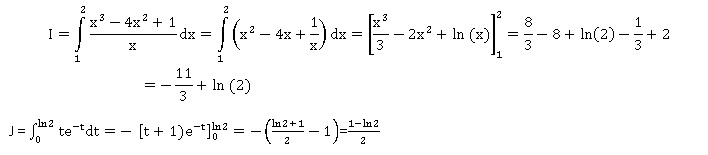
Suites numériques.
On considère la suite (u_n) définie pour tout entier naturel par u₀=-1 et u_n+1 = u_n/3+4.
1. Démontrer par récurence que cette suite est majorée par 6.
Initialisation : u₀ < 6 est vraie.
Hérédité : la propriété est supposée vraie au rang p : u_p < 6.
u_p+1 = u_p/3+4 ; u_p/3 < 2 ; par suite u_p+1 < 6.
Conclusion : la propriété est vraie au rang zéro et héréditaire. Donc cette suite est majorée par 6.
2. Soit la suite (vn) définie pour tout entiet n par v_n = u_n-6.
a. Montrer que la suite (v_n) est géométrique de raison 1/3 et de premier terme -7.
v_n+1 =u_n+1 -6=u_n / 3+4-6 =u_n/3-2=(u_n-6) /3 =v_n /3.
v₀ = u₀-6 = -7.
b. En déduire l'expression de v_n en fonction de n, puis l'expression de u_n en fonction de n.
v_n = v₀ / 3ⁿ = -7 / 3ⁿ ; u_n = v_n+6 = -7 / 3ⁿ +6.
c. Déterminer la limite de u_n quand n tend vers l'infini.
Quand n tend vers l'infini : 3ⁿ tend vers l'infini ; 1 / 3ⁿ tend vers zéro ; -7 / 3ⁿ tend vers zéro ;
u_n tend vers 6.

Géométrie analytique dans le plan.
Dans un repère orthonormé, on considère les points A(-2 ; 1) et B(3 ; -2).
a. Calculer AB.
AB = [x_B-x_A)² +(y_B-y_A)²]^½=(5²+(-3)²]^½=34^½.
b. Déterminer l'équation de la droite (AB).
y =ax +b.
La droite passe en A : 1 = -2a+b soit b = 1+2a.
Les coordonnées du point B vérifient l'équation de la droite : -2 = 3a+b.
-2=3a+1+2a ; a =-3/5 ; par suite b = -1/5.
y = -3/5x -1/5.
c. Déterminer l'équation du cercle de diamètre [AB].
Le centre du cercle se trouve au milieu du segment (AB] et ses coordonnées sont :
(x_A+x_B)/2 = 0,5 ; (y_A+y_B)/2 = -0,5.
Le rayon du cercle est R = [AB] /2 = 34^½/2.
Equation de ce cercle : ( x-0,5)² +(y+0,5)²=34/4 =17/2.

Géométrie analytique dans l'espace.
Dans l'espace on considère les points A(-2 ; 1 ; 1) ; B(0 ; 1 ;0) et C (-2 ; 2 ; 2).
1. Justifier que les points A, B et C définisent un plan..
2. Déterminer un vecteur normal au plan (ABC).
Ces trois points définissent un plan si et seulement si ils ne sont pas alignés.

3. En déduire une équation du plan (ABC).
0,5 k x -ky +kz = d.
A appartient à ce plan : -0,5*2k-k+k =d ; soit k = -d.
B appartient à ce plan : 0 -k +0=d ; soit k = -d .
C appartient à ce plan : -2*0,5 k-2k+2k=d ; k= -d.
Equation du plan (ABC) : 0,5 kx -ky +kz =-k soit 0,5x-y+z+1=0.

Matrice et système.
On conssidère le système suivant.
a. Ecrire la matriice A carrée d'ordre 3 associée au système.
b. Déterminer la matrice inverse A-1 à l'aide de la calculatrice.
c. Donner le calcul matriciel permettant d'obtenir le triplet solution.
d. Résoudre alors le système.

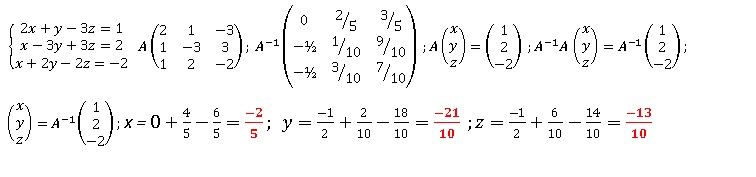
menu