Casser la craie, svp ! Concours interne ingénieur de l'industrie et des mines 2017. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . On modélise un bâton de craie comme un bloc de masse m relié à un ressort AB de raideur k ( très grande) et de longueur à vide négligeable. Un opérateur déplace l'extrémité B à la vitesse constante V de telle sorte que xB(t) = Vt +b0. On considère un mouvement sur une table horizontale. 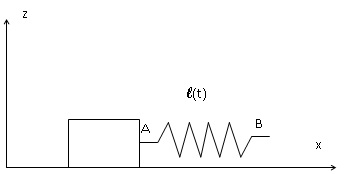L'abscisse du point A est notée x(t) et l(t) = xB(t) -x(t) désigne la longueur du ressort à l'instant t. le champ de pesanteur est uniforme ( g = 10 S.I ). 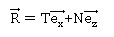Les réactions de contact exercées par la table sur le bloc  se réduisent à une force de contact satisfaisant aux lois de Coulomb avec un coefficient de frottement statique fS et un coefficient de frottement dynamique fD < fS. On observe que le bloc se déplace vers la droite avec une alternance de phases de glissement et de non glissement, appelé grippé-glissé. 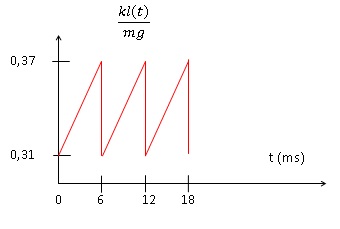Dans ces conditions, l'allongement du ressort a un comportement périodique décrit par le graphe suivant. B.1. Etablir l'expression de N et T en fonction des paramètres du problème et de X'. Solide immobile : Le poids et l'action normale du support se compensent : N = mg. La force de frottement compense la force exercée par le ressort. La longueur du ressort croît. T = k l(t)=k(xB(t) - x(t)) = k(Vt+b0-x(t)). T augmente jusqu'à ce que T = fS N = fS mg. Le solide se déplace : Quand T = fS mg, le solide commence à se déplacer. La force de frottement vaut F =fD mg, inférieure à T. T diminue jusqu'à ce que T = F et la masse s'arrète. B.2. On envisage une phase où le bloc est fixe sur le support. Comment varie l'allongement l du ressort en fonction du temps ? Identifier une telle phase sur le graphe fourni.  Exprimer T en fonction de k et l. En déduire la valeur lM de l en fonction de fS, m, g et k au moment ou le non-glissement cesse. Déduire du graphe la valeur  numérique de fS. l(t)=xB(t) - x(t) = Vt+b0-x(t). Sur le graphe, cela correspond au premier segment oblique dont la valeur absolue de la pente est la plus faible. T = k l(t)=k(xB(t) - x(t)) = k(Vt+b0-x(t)). T augmente jusqu'à ce que T = fS N = fS mg. fS mg.=k l M ; l M =fS mg./ k ; fS= k l M  /(mg) = 0,37. B.3. On prend comme origine des temps un instant où le bloc commence à se déplacer sur le support :  l(t=0) = lM ; x(t=0) = 0 et x'(t) =0) = v0. Ensuite  pour 0 < t < t1, x'(t) >0. Montrer que pour 0 < t < t1, on a l(t) = lM +Vt-x(t), puis établir que x(t) est solution de : x" +w2x=(fS-fD)g +w2Vt où w est une constante que l'on interprétera physiquement. l(t)=xB(t) - x(t) = Vt+b0-x(t). l(t=0)=lM=xB(t=0) - x(t=0) = b0. l(t)=Vt +lM-x(t). Ecrire la seconde loi de Newton sur l'axe des abscisses : -F+T = m x" ; -fD mg + kl(t) = m x". -fD mg + kVt + k lM-kx(t).= m x". x" + k / m x(t) = -fD g + k /mVt + k/ m lM. Or k / m lM =fS g ;  x" + k / m x(t) = -fD g + k /mVt + fS g . On pose w2 = k / m : x" +w2x=(fS-fD)g +w2Vt. (1).  w est la pulsation exprimée en rad s-1. B.4. Exprimer x(t) et x'(t) en fonction de t, w, V, fS et FD. Solution générale de x" +w2x=(fS-fD)g. x(t) est de la forme x(t) = A cos ( wt )+B sin ( wt )+ (fS-fD)g / w2. Solution générale de (1) :  x(t) = A cos ( wt )+B sin ( wt )+ (fS-fD)g / w2 +Vt. A et B sontt des constantes déterminées par les conditions initiales. x(t)=0 = 0  = A  +(fS-fD)g /w2  ; A = -(fS-fD)g /w2 . x'(t) = -Aw sin ( wt )+ Bw cos (wt)+V. x'(t=0)=v0=Bw +V  ; B = (v0-V) / w. x(t) = (fS-fD)g / w2 [ 1-cos ( wt )] +(v0-V) / w sin ( wt ) +Vt. x'(t) = (fS-fD)g /w sin ( wt ) +(v0-V)  cos ( wt )+V . B.5. Trouver la date t1 de la fin du glissement en fonction de w, V, g, fS et fD. x'(t1)=0. (v0-V) cos ( wt1 )+V =0. cos ( wt1 ) = V / (V-v0). B.6. On peut établir par le calcul  ( calcul non demandé ) que l(t1) = lm=(2fD -fS) mg / k. Déduire du graphe la valeur de fD et justifier l'approximation usuelle fS ~fD. klm /(mg)=0,31 =2fD-fS. fD=(0,31 +fS) / 2 = (0,31 +0,37) / 2 = 0,34. (fS-fD) / fS = 0,03 / 0,37 ~0,08 ( 8%). B.7. Comparer également sur le graphe les durées des phases de glissement et de non-glissement. La durée de la phase de non-glissement est très supérieure à la durée de la phase de glissement. B.8. Exprimer la fréquence n de l(t) en fonction de m, g, k, fS et fD. La période du mouvement est à peu près égale à la durée de la phase de non-glissement. T = mg(fS-fD) / k ; n = 1 / T = k / [mg(fS-fD)]. B.9. Dans le cas de la craie, on a n = 6 kHz : pour m = 50 g et V = 0,1 m/s. On suggère souvent de casser la craie en deux pour qu'elle ne crisse pas. Justifier ce procédé. En cassant la craie en deux, la masse est divisée par deux et k est multiplié par deux, la fréquence quadruple. L'oreille humaine perçoit les sons de fréquence comprise entre 20 Hz et 20 kHz. Le son devient inaudible.  .

menu