Mouvement sur
rouleaux,
Concours interne ingénieur de l'industrie et des mines 2017 .
Concours commun polytechnique 2011.
|
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
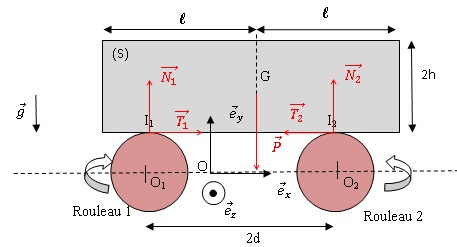
La rotation des rouleaux se fait sans frottement grâce à une liaison
parfaite. Le moment d'inertie relativement à l'axe d'un rouleau est
noté J=20 kg m 2.
Le rouleau 2 est entraîné par un moteur à la vitesse angulaire
constante w2
>0.
Les actions des rouleaux sur (S) en I 1 et I 2 sont
:
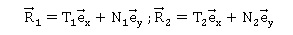
Les coefficients de frottement dynamique et statique en I 1
et I 2 sont égaux et valent : µ=0,1.
A t=0, le point G se situe sur la verticale de O tandis que l'extrémité
droite de (S) se situe à la verticale de O 2 et la vitesse du
solide (S) vaut V 0 = +0,442 m /s.
A.1. On suppose que
le mouvement de (S) s'effectue toujours sans glissement en I 1.
A un instant quelconque on note x(t) l'abscisse du point G. Ecrire la
relation qui résulte du non glissement.
Soient I 1S un point de (S) au voisinage de I 1
et I1R
un point du rouleau 1 au voisinage de I1. En absence de
glissement les points I1S et I1R
ont la même vitesse. Dans le référentiel du laboratoire :
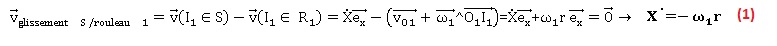 avec w1
négatif. avec w1
négatif.
Déterminer la vitesse de glissement de (S) en I2 en fonction
de X', r et w2.
Quel est le signe de T2 ? Ecrire la relation liant T2
et N2.
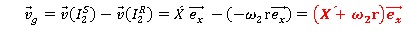 (2) (2)
X' et w2
sont positifs, la vitesse de glissement est dirigée vers la droite.
L'action tangentielle de frottement T2 est dirigée en sens
contraire de la vitesse de glissement.
T2 <0 ; µ = -T2 / N2. (3)
A.2. Etablir
deux
relations provenant du théorème de la résultante dynamique pour (S)
seul. Puis en considérant le rouleau 1 seul, établir une relation
provenant du moment dynamique en O.
(S) est soumis à 3 actions : son poids et les actions de contact en I1
et I2.
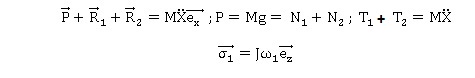 (4) (4)
Le rouleau 1 est soumis à son poids à R1 et à T1.
Seul le moment en O1 de T1 n'est pas nul.
Théorème du moment cinétique en O1 :
rT1 = J dw1/dt.(
5)
|
....
.....
|
A.3. Exprimer le moment cinétique en
G de (S) et en déduire une dernière relation.
(S) est en translation dans R. Dans le référentiel barycentrique, tous
les points de (S) sont immobiles. Les quantités de mouvement sont donc
nulles. Le moment cinétique en G de
(S) est donc nul.
Théorème du moment cinétique au point G.
La dérivée du moment cinétique en G est égale à la somme des moments
des forces extérieures en G.
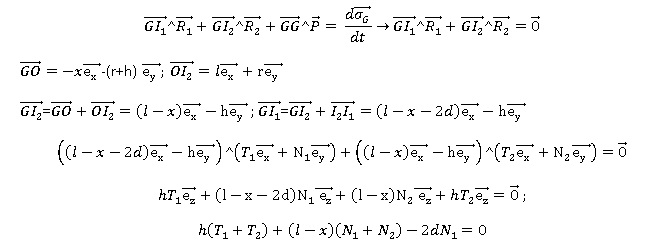
Relation 6.
A.4. Des relations précédentes
obtenir une équation différentielle en X(t).
(5) donne : T1 = J /r dw1/dt.
(1) donne T1 = - J /r dX'/dt
= -J / r2 X".
(4) donne T2 = MX"-T1 = (M +J / r2)X".
(3) donne : N2 = -T2 /µ = - (M +J / r2)
/ µ X".
N1 = Mg-N2 = Mg + (M +J / r2) / µ X".
(6) donne :
h( -J / r2
X" + (M +J / r2) X") +(l-x)Mg -2d(Mg + (M +J / r2) / µ X") =0.
hM X" +(l-x)Mg -2d(Mg + (M +J / r2) / µ X")=0.
X" hM - 2d( (M +J / r2) / µ)+(l-2d)Mg -Mg X =0.
X" (hM - 2d( (M +J / r2) / µ)+(l
-2d-X)Mg =0.
X" +(l
-2d-X)Mg / [ hM - 2d( (M +J / r2) / µ ] X =0.
A.5. vérifier que
cette équation est bien celle d'un oscillateur harmonique de position
d'équilibre Xe et de pulsation W.
On pose W2
=Mg / [- hM + 2d( (M +J / r2) / µ ] et -Xe
= 2d-l.
X" +W2
(X -Xe)=0.
A.N. M = 3500 kg ;
r = 0,2 m ; 2d = 1,6 m ; 2 l
= 2 m ; h = 0,4 m ; J = 20 kg m2 ; µ= 0,1.
W =
0,74 rad /s ; Xe = 1,6-1=0,60 m.
|
|
|
A.6. A l'instant t = t, la vitesse de (S)
s'annule pour la première fois. Etablir l'expression de tan ( Wt) en fonction de W, l, d et V0.
Calculer l'amplitude maximale Xm du déplacement de G et en
déduire que
(S) est toujours en appui sur le rouleau n°1 à l'instant t = t.
X +Xe= A
cos (Wt) + B sin (Wt).
A l'instant initial, X = 0 et X'(t=0) = V0 = 0,442 m /s.
Xe = A.
X'(t) = -AW sin (Wt) + B W cos ( Wt).
V0 = B W.
X(t) = -Xe(1-cos (Wt) + V0 / W sin (Wt).
La vitesse s'annule à t = t.
0 = -XeW sin (Wt)
+ V0
cos ( Wt).
tan ( Wt)
= V0 / (Xe W).
t = 1
/ W arctan ( V0
/ (Xe W)).
A.N. tan ( Wt)
=0,442 /(0,6 x0,74) =0,995 ~1.
Wt
~ p / 4.
La vitesse étant positive entre les dates 0 et t.
Xm = X(t)
= -Xe(1-cos (p / 4) + V0 / W sin (p / 4).
Xm =
-0,6(1-0,707) +0,442 / 0,74 x 0,707 = - 0,1757 +0,4223 ~0,25 m.
Xm est inférieur à 2l-2d = 2-1,6 = 0,40. Il y
a donc toujours appui sur le rouleau 1.
|
|
|
|
A.7. Vérifier
également que le mouvement de (S) reste bien sans glissement jusqu'à
l'instant t = t.|
< µ.
Il a non glissement en I1 si | T1 / N1|
< µ.
X" = - W2(X
+Xe).
| T1 / N1| =[J / r2
|X"| ] / (Mg + (M +J / r2) / µ X"] = [J / r2 W2(X +Xe) ] / (Mg - (M +J / r2) / µ W2(X +Xe)] .
Le numérateur [J / r2 W2(X +Xe) ] est maximal pour X = Xm.
Le dénominateur (Mg - (M +J / r2) / µ W2(X +Xe)
est minimal pour X = Xm.
| T1 / N1| est maximal pour X = Xm.
| T1 / N1|max = [J / r2
W2(Xm +Xe) ] / (Mg - (M +J / r2) / µ W2(Xm
+Xe)].
A.N :
| T1 / N1|max =[20 / 0,22
x0,742(0,25+0,6) ] / (3500 x9,81 - (3500 +20 / 0,22) / 0,1x 0,742(0,25+0,6) ].
| T1 / N1|max =232,73 / 18618 =0,0125,
valeur inférieur à µ=0,1.
A.8. Etablir les expressions des
composantes T2(X) et N2(X) de la réaction en I2.
T2
= MX"-T1 = (M +J / r2)X" = - (M +J / r2)W2(X +Xe).
N2
= -T2 /µ = - (M +J / r2)
/ µ X" = (M +J / r2)W2(X +Xe)
/ µ.
A.9. Exprimer le
travail fourni par le moteur d'entraînement au rouleau 2 entre les
dates 0 et t.
Le rouleau 2 est soumis à :
son poids, appliqué en O2. Le poids ne travaille pas et son
moment par rapport à l'axe de rotation est nul.
Au couple exercé par le moteur de moment moteur . Le travail de ce couple
est positif.
à la réaction -R2 exercée en I2, fournissant un
travail négatif.
La vitesse de rotation du rouleu 2 est constante. Le moment cinétique
est constant et le moment dynamique est nul.
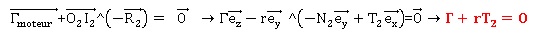
Puissance fournie par le moteur : Pm = G w2 = -T2
r w2 positif.
Pm = - (M +J / r2)X" r w2 .
Travail élémentaire d W = Pm dt = - (M +J / r2) r w2 dX'.
Intégrer entre 0 et t.
W = (M +J / r2) r w2 V0
.
|
|